修改时间:2021-05-20 浏览次数:990 类型:二轮复习
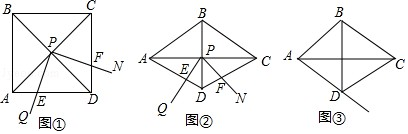
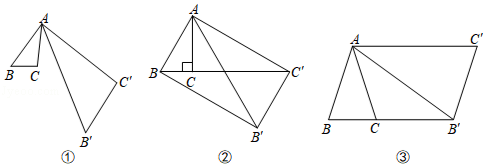
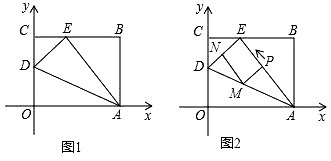
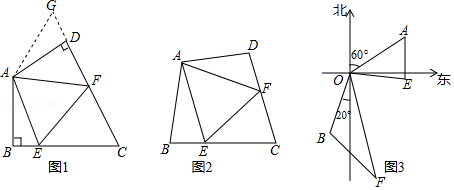
李明同学一时没有思路,当他认真分析题目信息后,发现以PA、PB、PC的长为边的三角形是直角三角形,他突然有了正确的思路:如图2,将△BPC绕点B逆时针旋转60°,得到△BP′A.连接PP',易得△P′PB是正三角形,△P′PA是直角三角形,则得∠BPC=;
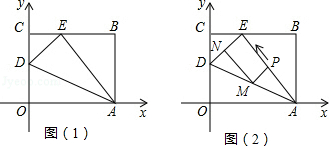
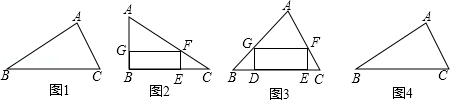
如图2,在Rt△ABC中,AB=6,BC=8,∠B=90°.矩形BEFG是△ABC的内接矩形,若EF=2,则矩形BEFG的面积为.
如图3,在△ABC中,AB=6 ,BC=8,∠B=45°,矩形DEFG是△ABC的一个内接矩形且D、E在边BC上.若EF=2,求矩形DEFG的面积;
问题解决:

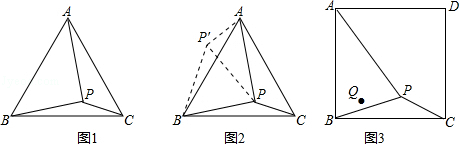
如图①,是一张直角三角形纸片,∠B=90°,小明想从中剪出一个以∠B为内角且面积最大的矩形,经过多次操作发现,当沿着中位线DE、EF剪下时,所得的矩形的面积最大,随后,他通过证明验证了其正确性,并得出:矩形的最大面积与原三角形面积的比值为.
如图②,在△ABC中,BC=a,BC边上的高AD=h,矩形PQMN的顶点P、N分别在边AB、AC上,顶点Q、M在边BC上,则矩形PQMN面积的最大值为.(用含a,h的代数式表示)
如图③,有一块“缺角矩形”ABCDE,AB=30,BC=40,AE=20,CD=16,小明从中剪出了一个面积最大的矩形(∠B为所剪出矩形的内角),求该矩形的面积.
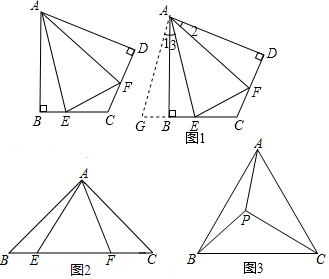
小明想到条件∠EAF= ∠BAD应用需要转化,将△ADF绕顶点A旋转到△ABG处,此时△ABG≌△ADF,把线段BE、FD集中到一起,进一步可以再证明EF=EG=BE+FD.
证明:延长EB到G,使BG=DF,连接AG.
∵∠ABG=∠ABC=∠D=90°,
AB=AD
∴△ABG≌△ADF.
小明没有证明结束,请你补齐证明过程.
基本运用:请你用第(1)题的解答问题的思想方法,解答下面的问题
求证:EF2=BE2+CF2;
拓展延伸

截长法与补短法在证明线段的和、差、倍、分等问题中有着广泛的应用.具体的做法是在某条线段上截取一条线段等于某特定线段,或将某条线段延长,使之与某特定线段相等,再利用全等三角形的性质等有关知识来解决数学问题.
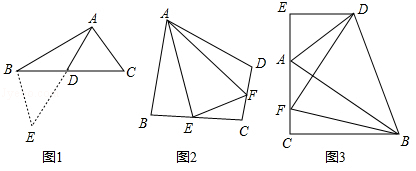
解决此问题可以用如下方法:延长AD到点E使DE=AD,再连接BE,把AB、AC、2AD集中在△ABE中.利用三角形三边的关系即可判断中线AD的取值范围是;
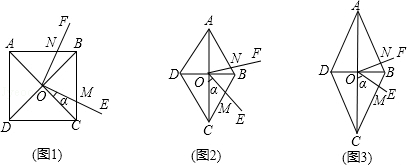
如图2,在四边形ABCD中,AB=AD,∠ABC+∠ADC=180°,E、F分别是边BC,边CD上的两点,且∠EAF= ∠BAD,求证:BE+DF=EF.
如图3,在△ABC中,∠ACB=90°,∠CAB=60°,点D是△ABC外角平分线上一点,DE⊥AC交CA延长线于点E,F是AC上一点,且DF=DB.
求证:AC﹣AE= AF.
试题篮