修改时间:2021-05-20 浏览次数:1243 类型:二轮复习

①在运动过程中,是否存在这样的t值,使⊙P正好与四边形ABCD的一边(或边所在的直线)相切?若存在,求出t值;若不存在,请说明理由.
②若⊙P与四边形BCQP至多有两个共公点,请直接写出t的取值范围.

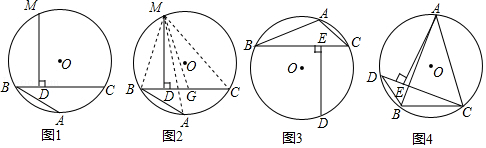
证明:如图2,在CB上截取CG=AB,连接MA,MB,MC和MG
∵M是 的中点,
∴MA=MC
……
①如图3,已知△ABC内接于⊙O,BC>AB>AC,D是 的中点,依据阿基米德折弦定理可得图中某三条线段的等量关系为;
②如图4,已知等腰△ABC内接于⊙O,AB=AC,D为 上一点,连接DB,∠ACD=45°,AE⊥CD于点E,△BCD的周长为4
+2,BC=2,请求出AC的长.
请阅读下列材料,完成相应的任务:

下面是该定理的证明过程.
已知:如图1,四边形ABCD内接于⊙O.

求证:AB•DC+AD•BC=AC•BD
证明:如图2,作∠BAE=∠CAD,交BD于点E,
∵ =
,
∴∠ABE=∠ACD,
∴△ABE∽△ACD,
∴ ,
∴AB•DC=AC•BE,
∵ =
,
∴∠ACB=∠ADE.( )※
∵∠BAE=∠CAD,
∴∠BAE+∠EAC=∠CAD+∠EAC,即∠BAC=∠EAD,
∴△ABC∽△AED,
∵AD•BC=AC•ED,
∴AB•DC+AD•BC=AC•BE+AC•ED=AC(BE+ED)=AC•BD.
如图1,四边形ABCD中,若AC=BD,AC⊥BD,则称四边形ABCD为“等垂四边形.根据等垂四边形对角线互相垂直的特征可得等垂四边形的一个重要性质:等垂四边形的面积等于两条对角线乘积的一半.根据以上信息解答下列问题:


(i)作∠ADF=∠AED,交CA的延长线于点F(如图③),求证:DF为 Rt△ACD的外接圆的切线.
(ii)如图④,点G在BC的延长线上,∠BGE=∠BAC,已知sin∠AED= ,AD=1,求DG的长..

A(1,0)的距离跨度;
B(﹣ ,
)的距离跨度;
C(﹣3,﹣2)的距离跨度;
②根据①中的结果,猜想到图形G1的距离跨度为2的所有的点组成的图形的形状是.

【回归课本】我们曾学习过这样的基本事实:①线段垂直平分线上的点到线段两端的距离相等;②同弧所对的圆周角相等.
【初步体验】如图,已知△ABC,用没有刻度的直尺和圆规作图,不要求写作法,但要保留作图痕迹,并对作图中涉及到的点用字母进行标注.
如图③,已知线段a和等边△ABC,作△BCM,使∠BMC=∠BAC,BM+CM=a.
他的做法是:
1画△ABC的外接圆;
2以A为圆心、AB长为半径画⊙A;
3以C为圆心、a为半径画弧与⊙A交于点F;
4连接CF与△ABC的外接圆交于点M,则△BCM是要画的三角形.
请你给出证明,并直接写出这样的点M有个.
如图④,已知线段b和△ABC,作△BCN,使∠BNC=∠BAC,BN﹣CN=b.

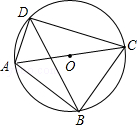
解法1.∵AE是⊙O的直径,∴∠ADE=90°=∠C,∴DE∥BC
又∵D是AC的中点,∴ =
=
=
,∴E是AB的中点,∴DE=
BC=3.
在Rt△ADE中,设AD=4x,AE=5x,∴(4x)2+32=(5x)2 ,
解之得:x1=1,x2=﹣1(舍去),∴AE=5x=5,即⊙O的直径为5.
解法2.∵∠A+∠CDB=90°,又∵∠A+∠CBA=90°,∴∠CDB=∠CBA,∠C=∠C,
∴△DCB∽△BCA,∴ =
,∴BC2=DC•AC,又∵AC=2DC=2AD,∴BC2=AD•2AD,
AD= AE,62=2×(
AE)2 , AE=
.
以上两种解法结果不同,那么问题出在哪里呢?
①下列说法正确的是。
A.解法1有错 B.解法2有错 C.解法1、2都有错
D.解法1、2都没错,但题中条件“AD:AE=4:5”是多余的
②在①中若你选择的是A、B、C中一个,请说明错在哪里?若你选的是D,请删去“AD;AE=4:5”这个条件,求出⊙O的直径.
①有两个相等的实数根; ②有两个不相等的实数根; ③没有实数根.
试题篮