题型:综合题 题类:常考题 难易度:普通
浙教版2019中考数学复习专题之圆综合题
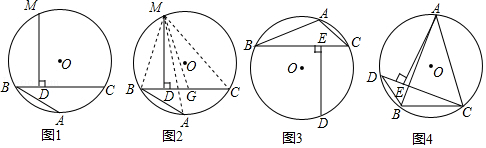
证明:如图2,在CB上截取CG=AB,连接MA,MB,MC和MG
∵M是 的中点,
∴MA=MC
……
①如图3,已知△ABC内接于⊙O,BC>AB>AC,D是 的中点,依据阿基米德折弦定理可得图中某三条线段的等量关系为;
②如图4,已知等腰△ABC内接于⊙O,AB=AC,D为 上一点,连接DB,∠ACD=45°,AE⊥CD于点E,△BCD的周长为4
+2,BC=2,请求出AC的长.
试题篮