修改时间:2022-11-02 浏览次数:261 类型:二轮复习
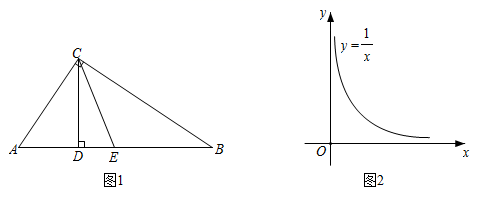
①分别求线段 、
的长(用含a、b的代数式表示);
②比较大小: ▲
(填“<”、“=”或“>”),并用含a、b的代数式表示该大小关系.
①当 时,
▲ ;当
时, ▲ ;
②通过归纳猜想,可得l的最小值是 ▲ .请利用图2构造恰当的图形,并说明你的猜想成立.
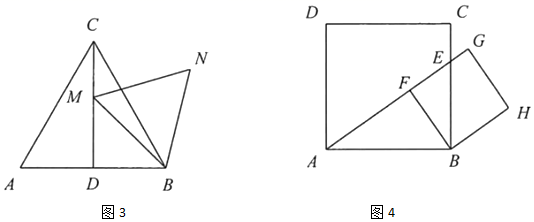
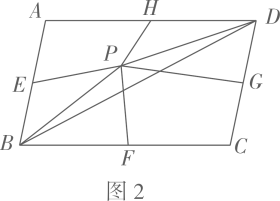
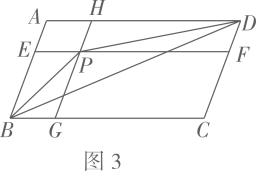
小华同学给出了图1的面积平分线的一个作图方案:如图2,将这个L图形分成矩形AGEF、矩形GBCD,这两个矩形的对称中心O1 , O2所在直线是该L图形的面积平分线.请用无刻度的直尺在图1中作出其他的面积平分线.(作出一种即可,不写作法,保留作图痕迹)
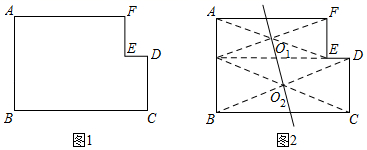
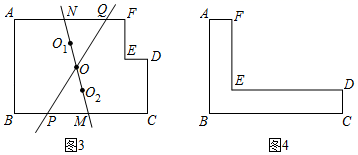
如图3,直线O1O2是小华作的面积平分线,它与边BC,AF分别交于点M,N,过MN的中点O的直线分别交边BC,AF于点P,Q,直线PQ(填“是”或“不是”)L图形ABCDEF的面积平分线.
在L图形ABCDEF形中,已知AB=4,BC=6.
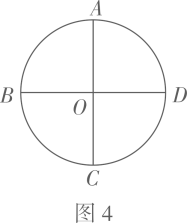
如图4,CD=AF=1.
①该L图形的面积平分线与两条水平的边分别相交于点P,Q,求PQ长的最大值;
②该L图形的面积平分线与边AB,CD分别相交于点G,H,当GH的长取最小值时,BG的长为 ▲ .
学完《全等三角形》一章后,我们知道“斜边和一条直角边分别相等的两个直角三角形全等(简称HL定理)”是判定直角三角形全等的特有方法.

如图(1),在△ABC中,∠BAC=90°,AB=AC,点D、E分别在边AC、AB上.若CE=BD,则线段AE和线段AD的数量关系是.
在△ABC中,∠BAC= (90°<
<180°),AB=AC=m,点D在边AC上.
若点E在边AB上,且CE=BD,如图(2)所示,则线段AE与线段AD相等吗?如果相等,请给出证明;如果不相等,请说明理由.
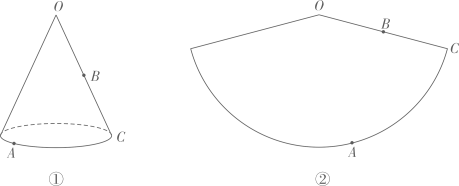
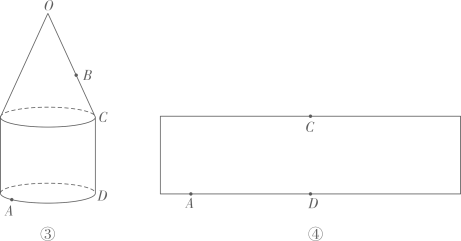
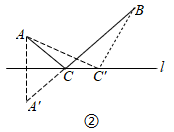
①蚂蚁从点A爬行到点O的最短路径的长为 ▲ (用含l,h的代数式表示).
②设 的长为a,点B在母线
上,
.圆柱的侧面展开图如图④所示,在图中画出蚂蚁从点A爬行到点B的最短路径的示意图,并写出求最短路径的长的思路.
|
已知线段 ( 1 )这样的点A唯一吗? ( 2 )点A的位置有什么特征?你有什么感悟? |
“追梦”学习小组通过操作、观察、讨论后汇报:点A的位置不唯一,它在以 为弦的圆弧上(点B、C除外),…….小华同学画出了符合要求的一条圆弧(如图1).
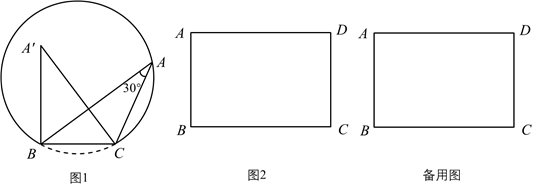
①该弧所在圆的半径长为;
② 面积的最大值为;
①线段 长的最小值为;
②若 ,则线段
长为.
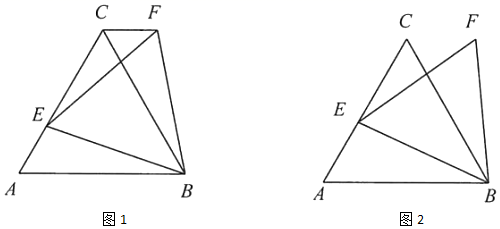
有一组对角互余的凸四边形称为对余四边形,连接这两个角的顶点的线段称为对余线.

如图①,对余四边形ABCD中,AB=5,BC=6,CD=4,连接AC.若AC=AB,求sin∠CAD的值;
在平面直角坐标系中,点A(﹣1,0),B(3,0),C(1,2),四边形ABCD是对余四边形,点E在对余线BD上,且位于△ABC内部,∠AEC=90°+∠ABC.设 =u,点D的纵坐标为t,请直接写出u关于t的函数解析式.

①生市保护区是正方形区城,位置如图③所示
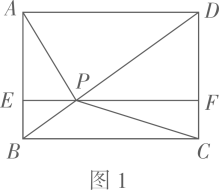
②生态保护区是圆形区域,位置如图④所示.
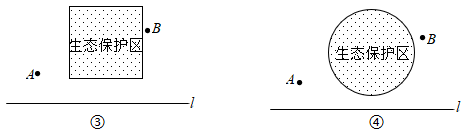

①过点E画垂直于y轴的直线m,则⊙O关于直线m的“远点”是点_▲__(填“A”、“B”、“C”或“D”),⊙O关于直线m的“特征数”为_▲__;
②若直线n的函数表达式为 ,求
关于直线n的“特征数”;
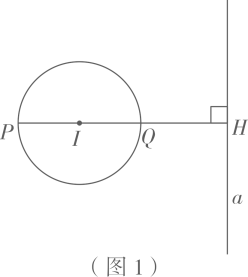
①半径为 的圆:;
②如图,上方是半径为 的半圆,下方是正方形的三条边的“窗户形“:;
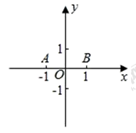
①若 ,用直尺和圆规画出点
所在的区域并求它的面积(所在区域用阴影表示);
②若点 在⊙
上运动,⊙
的半径为
,圆心
在过点
且与
轴垂直的直线上.对于⊙
上任意点
,都有
,直接写出圆心
的横坐标
的取值范围.
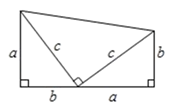
如图,两个边长分别为 、
、
的直角三角形和一个两条直角边都是
的直角三角形拼成一个梯形.用两种不同的方法计算梯形的面积,并写出你发现的结论;

边形有
个顶点,在它的内部再画
个点,以(
)个点为顶点,把
边形剪成若干个三角形,设最多可以剪得
个这样的三角形.当
,
时,如图,最多可以剪得
个这样的三角形,所以
.
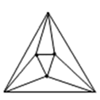
①当 ,
时,如图,
;当
,
时,
;
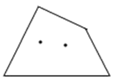
②对于一般的情形,在 边形内画
个点,通过归纳猜想,可得
(用含
、
的代数式表示).请对同一个量用算两次的方法说明你的猜想成立.
试题篮