修改时间:2022-03-10 浏览次数:212 类型:二轮复习



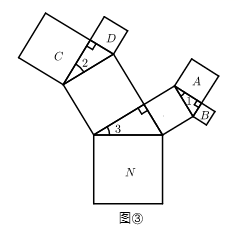
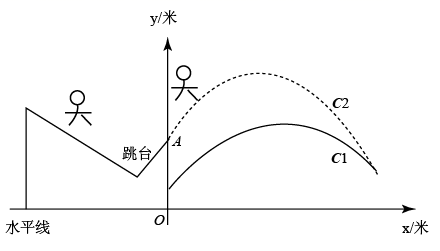
数学实践活动,是一种非常有效的学习方式.通过活动可以激发我们的学习兴趣,提高动手动脑能力,拓展思推空间,丰富数学体验.让我们一起动手来折一折、转一转、剪一剪,体会活动带给我们的乐趣.
折一折:将正方形纸片ABCD折叠,使边AB、AD都落在对角线AC上,展开得折痕AE、AF , 连接EF , 如图1.
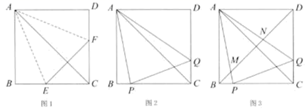
线段BP、PQ、DQ之间的数量关系为;
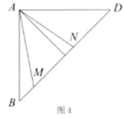
求证: .
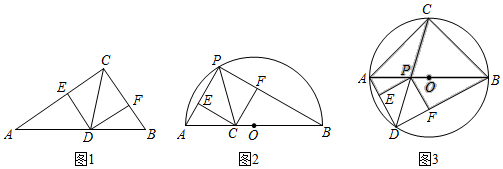
如图1,在Rt△ABC中,∠ACB=90°,AC>BC,∠ACB的平分线交AB于点D.过点D分别作DE⊥AC,DF⊥BC.垂足分别为E,F,则图1中与线段CE相等的线段是.
如图2,AB是半圆O的直径,AB=8.P是 上一点,且
,连接AP,BP.∠APB的平分线交AB于点C,过点C分别作CE⊥AP,CF⊥BP,垂足分别为E,F,求线段CF的长.
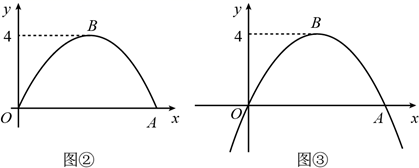
如图3,是某公园内“少儿活动中心”的设计示意图.已知⊙O的直径AB=70m,点C在⊙O上,且CA=CB.P为AB上一点,连接CP并延长,交⊙O于点D.连接AD,BD.过点P分别作PE⊥AD,PF⊥BD,重足分别为E,F.按设计要求,四边形PEDF内部为室内活动区,阴影部分是户外活动区,圆内其余部分为绿化区.设AP的长为x(m),阴影部分的面积为y(m2).
①求y与x之间的函数关系式;
②按照“少儿活动中心”的设计要求,发现当AP的长度为30m时,整体布局比较合理.试求当AP=30m时.室内活动区(四边形PEDF)的面积.
试题篮