修改时间:2022-04-13 浏览次数:128 类型:复习试卷

①∠BAD的度数是 ;
②当旋转时间x=秒时,射线BN过点A;
①如图3,若点P在CD与EF之间,且∠APB=126°,求旋转时间x的值;
②若旋转时间x<24,求∠APB的度数(直接写出用含x的代数式表示的结果).

解:过点P作PM∥AB
∵AB∥CD(已知)
∴PM∥CD,
∴∠B+∠1=180°,.
∴∠C+∠2=180°
∵∠BPC=∠1+∠2
∴∠B+∠C+∠BPC=360°
【问题情境】
王老师组织同学们开展了探究三角之间数量关系的数学活动.
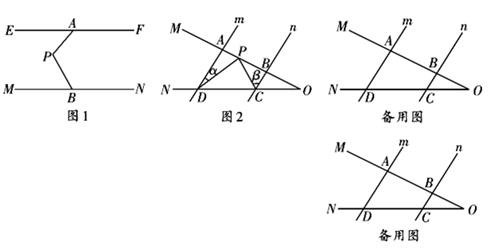
如图2,射线OM与射线ON交于点O,直线m∥n,直线m分别交OM、ON于点A、D,直线n分别交OM、ON于点B、C,点P在射线OM上运动.
①当点P在A、B(不与A、B重合)两点之间运动时,设∠ADP=∠α,∠BCP=∠β.则∠CPD,∠α,∠β之间有何数量关系?请说明理由;
②若点P不在线段AB上运动时(点P与点A、B、O三点都不重合),请你画出满足条件的所有图形并直接写出∠CPD,∠α,∠β之间的数量关系.

证明:过点E作EF∥AB,
∵AB∥CD(已知),EF∥AB(辅助线的作法),
∴EF∥CD( ),
∴∠C=∠CEF( ),
∵EF∥AB(作图),
∴∠B= ▲ , ( ),
∴∠B+∠C=_ ▲ (等量代换),即∠B+∠C=∠BEC.
在同一平面内的两条直线有相交和平行两种位置关系.
如图1,若AB∥CD,点P在AB,CD外部,则有∠B=∠BOD.
又因为∠BOD是△POD的外角,则有∠BOD=∠BPD+∠D,
所以∠BPD=∠B-∠D

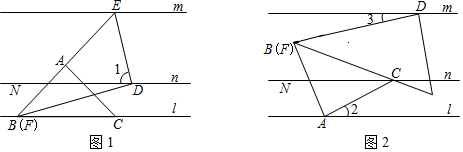
操作发现
结论应用
阅读下面内容,并解答问题
已知:如图1, ,
. 求证:
.
老师要求学生在完成这道教材上的题目证明后,尝试对图形进行变式,继续做拓展探究,看看有什么新发现?

请你在小颖操作探究的基础上,继续完成下面的问题:
①猜想图①中、
与
之间的数量关系并加以证明;
②利用图③探究,在拖动点至
的上方或
的下方时,
、
与
之间还存在其它数量关系,请直接写出
、
与
之间的数量关系: ▲ (写出一种即可).

试题篮