修改时间:2021-11-16 浏览次数:144 类型:复习试卷
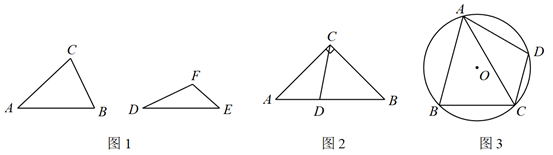
如图,已知 中,AB=AC=m,BC=n,
,点P为平面内不与点A、C重合的任意一点,将线段CP绕点P顺时针旋转a,得线段PD,E、F分别是CB、CD的中点,设直线AP与直线EF相交所成的较小角为β,探究
的值和
的度数与m、n、α的关系,请你参与学习小组的探究过程,并完成以下任务:
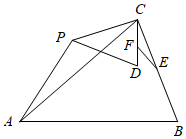
小明研究了 时,如图1,求出了
,
;
小红研究了 时,如图2,求出了
,
;
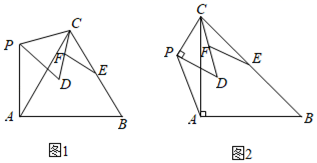
他们又共同研究了α=120°时,如图3,也求出了 ;
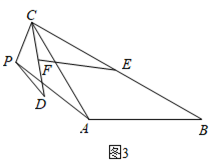
归纳总结:
最后他们终于共同探究得出规律:
(用含m、n的式子表示);
(用含α的式子表示).
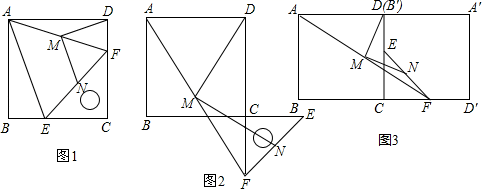
①平行四边形;②矩形;③菱形;④正方形.
①求 的值;
②若 ,
,求△ABC和△ADC的周长之差.
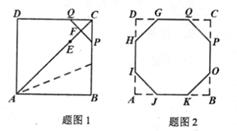
解:理由如下:
① 
∴∠GQP=135°
同理可得:∠QPO=∠POK=∠OKJ=∠KJI=∠JIH=∠IHG=∠HGQ=135°。
② 
∴PQ=QG。
同理可得:QG=GH=HI=IJ=JK=KO=PO=PQ
∴八边形GHIJKOPQ是正八边形。
试题篮