全国历年中考数学真题精选汇编：图形变换与视图2

修改时间：2021-07-12 浏览次数：110 类型：二轮复习编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、单选题

1. 如图， $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点D是边BC的中点，以AD为底边在其右侧作等腰三角形ADE，使 $\text{[math]}$ ，连结CE，则 $\text{[math]}$ 的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 2

查看解析收藏纠错

+选题
2. 如图，点P是函数 $\text{[math]}$ 的图像上一点，过点P分别作x轴和y轴的垂线，垂足分别为点A、B，交函数 $\text{[math]}$ 的图像于点C、D，连接 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ ，其中 $\text{[math]}$ ，下列结论：① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ ，其中正确的是（）

A . ①② B . ①③ C . ②③ D . ①

查看解析收藏纠错

+选题

二、填空题

3. 如图，在正方形 $\text{[math]}$ 中，点O是对角线 $\text{[math]}$ 的中点，点P在线段 $\text{[math]}$ 上，连接 $\text{[math]}$ 并延长交 $\text{[math]}$ 于点E，过点P作 $\text{[math]}$ 交 $\text{[math]}$ 于点F，连接 $\text{[math]}$ 、 $\text{[math]}$ ， $\text{[math]}$ 交 $\text{[math]}$ 于G，现有以下结论：① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ ；④ $\text{[math]}$ 为定值；⑤ $\text{[math]}$ .以上结论正确的有（填入正确的序号即可）.

查看解析收藏纠错

+选题
4. 如图，四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 于点D.若 $\text{[math]}$ ， $\text{[math]}$ ，则线段 $\text{[math]}$ 的长为.

查看解析收藏纠错

+选题
5. 如图、在正六边形 $\text{[math]}$ 中，连接线 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 交于点M， $\text{[math]}$ 与 $\text{[math]}$ 交于点为N， $\text{[math]}$ 与 $\text{[math]}$ 交于点O，分别延长 $\text{[math]}$ ， $\text{[math]}$ 于点G，设 $\text{[math]}$ .有以下结论：① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ 的重心、内心及外心均是点M；④四边形 $\text{[math]}$ 绕点O逆时针旋转 $\text{[math]}$ 与四边形 $\text{[math]}$ 重合.则所有正确结论的序号是.

查看解析收藏纠错

+选题
6. 图1是邻边长为2和6的矩形，它由三个小正方形组成，将其剪拼成不重叠、无缝隙的大正方形（如图2），则图1中所标注的 $\text{[math]}$ 的值为；记图1中小正方形的中心为点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，图2中的对应点为点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .以大正方形的中心 $\text{[math]}$ 为圆心作圆，则当点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 在圆内或圆上时，圆的最小面积为.

查看解析收藏纠错

+选题
7. 如图，在矩形 $\text{[math]}$ 中，点E在边 $\text{[math]}$ 上， $\text{[math]}$ 与 $\text{[math]}$ 关于直线 $\text{[math]}$ 对称，点B的对称点F在边 $\text{[math]}$ 上，G为 $\text{[math]}$ 中点，连结 $\text{[math]}$ 分别与 $\text{[math]}$ 交于M，N两点，若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的长为， $\text{[math]}$ 的值为.

查看解析收藏纠错

+选题
8. 如图，在△ABC中，∠BAC＝30°，∠ACB＝45°，AB＝2，点P从点A出发沿AB方向运动，到达点B时停止运动，连结CP ，点A关于直线CP的对称点为A′，连结A′C ， A′P ．在运动过程中，点A′到直线AB距离的最大值是；点P到达点B时，线段A′P扫过的面积为．

查看解析收藏纠错

+选题

三、解答题

9. 小王在学习浙教版九上课本第72页例2后，进一步开展探究活动：将一个矩形ABCD绕点A顺时针旋转α（0°＜α≤90°），得到矩形AB′C′D′，连结BD ．

[探究1]如图1，当α＝90°时，点C′恰好在DB延长线上．若AB＝1，求BC的长．

[探究2]如图2，连结AC′，过点D′作D′M∥AC′交BD于点M ．线段D′M与DM相等吗？请说明理由．

[探究3]在探究2的条件下，射线DB分别交AD′，AC′于点P ， N（如图3），发现线段DN ， MN ， PN存在一定的数量关系，请写出这个关系式，并加以证明．

查看解析收藏纠错

+选题

四、综合题

10. 如图1，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点D是 $\text{[math]}$ 边上一点（含端点A、B），过点B作 $\text{[math]}$ 垂直于射线 $\text{[math]}$ ，垂足为E，点F在射线 $\text{[math]}$ 上，且 $\text{[math]}$ ，连接 $\text{[math]}$ 、 $\text{[math]}$ .

（1）求证： $\text{[math]}$ ；

（2）如图2，连接 $\text{[math]}$ ，点P、M、N分别为线段 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 的中点，连接 $\text{[math]}$ 、
$\text{[math]}$ 、 $\text{[math]}$ .求 $\text{[math]}$ 的度数及 $\text{[math]}$ 的值；

（3）在（2）的条件下，若 $\text{[math]}$ ，直接写出 $\text{[math]}$ 面积的最大值.

查看解析收藏纠错

+选题

11. 如图1，在平面直角坐标系 $\text{[math]}$ 中，抛物线 $\text{[math]}$ 与x轴分别相交于A、B两点，与y轴相交于点C，下表给出了这条抛物线上部分点 $\text{[math]}$ 的坐标值：

x	…	$\text{[math]}$	0	1	2	3	…
y	…	0	3	4	3	0	…

（1）求出这条抛物线的解析式及顶点M的坐标；

（2） $\text{[math]}$ 是抛物线对称轴上长为1的一条动线段（点P在点Q上方），求 $\text{[math]}$ 的最小值；

（3）如图2，点D是第四象限内抛物线上一动点，过点D作 $\text{[math]}$ 轴，垂足为F， $\text{[math]}$ 的外接圆与 $\text{[math]}$ 相交于点E.试问：线段 $\text{[math]}$ 的长是否为定值？如果是，请求出这个定值；如果不是，请说明理由.

查看解析收藏纠错

+选题

12. 已知正方形ABCD与正方形AEFG，正方形AEFG绕点A旋转一周.

（1）如图①，连接BG、CF，求 $\text{[math]}$ 的值；

（2）当正方形AEFG旋转至图②位置时，连接CF、BE，分别去CF、BE的中点M、N，连接MN、试探究：MN与BE的关系，并说明理由；

（3）连接BE、BF，分别取BE、BF的中点N、Q，连接QN，AE=6，请直接写出线段QN扫过的面积.

查看解析收藏纠错

+选题
13. 在矩形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，F是对角线 $\text{[math]}$ 上不与点A，C重合的一点，过F作 $\text{[math]}$ 于E，将 $\text{[math]}$ 沿 $\text{[math]}$ 翻折得到 $\text{[math]}$ ，点G在射线 $\text{[math]}$ 上，连接 $\text{[math]}$ .

（1）如图1，若点A的对称点G落在 $\text{[math]}$ 上， $\text{[math]}$ ，延长 $\text{[math]}$ 交 $\text{[math]}$ 于H，连接 $\text{[math]}$ .

①求证： $\text{[math]}$ ；

②求 $\text{[math]}$ .

（2）如图2，若点A的对称点G落在 $\text{[math]}$ 延长线上， $\text{[math]}$ ，判断 $\text{[math]}$ 与 $\text{[math]}$ 是否全等，并说明理由.

查看解析收藏纠错

+选题
14. 如图，直线 $\text{[math]}$ 与x轴交于点B，与y轴交于点A，点P为线段 $\text{[math]}$ 的中点，点Q是线段 $\text{[math]}$ 上一动点（不与点O、A重合）.

（1）请直接写出点A、点B、点P的坐标；

（2）连接 $\text{[math]}$ ，在第一象限内将 $\text{[math]}$ 沿 $\text{[math]}$ 翻折得到 $\text{[math]}$ ，点O的对应点为点E.若 $\text{[math]}$ ，求线段 $\text{[math]}$ 的长；

（3）在（2）的条件下，设抛物线 $\text{[math]}$ 的顶点为点C.
①若点C在 $\text{[math]}$ 内部（不包括边），求a的取值范围；

②在平面直角坐标系内是否存在点C，使 $\text{[math]}$ 最大？若存在，请直接写出点C的坐标；若不存在，请说明理由.

查看解析收藏纠错

+选题
15. 如图，

（1）【推理】
如图1，在正方形ABCD中，点E是CD上一动点，将正方形沿着BE折叠，点C落在点F处，连结BE，CF，延长CF交AD于点G.
求证： $\text{[math]}$ .

（2）【运用】
如图2，在（推理）条件下，延长BF交AD于点H.若 $\text{[math]}$ ， $\text{[math]}$ ，求线段DE的长.

（3）【拓展】
将正方形改成矩形，同样沿着BE折叠，连结CF，延长CF，BF交直线AD于G，两点，若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的值（用含k的代数式表示）.

查看解析收藏纠错

+选题
16. 某数学兴趣小组在数学课外活动中，对多边形内两要互相垂直的线段做了如下探究：
（观察与猜想）

（1）如图1，在正方形 $\text{[math]}$ 中，点 $\text{[math]}$ ， $\text{[math]}$ 分别是 $\text{[math]}$ ， $\text{[math]}$ 上的两点，连接 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的值为；

（2）如图2，在矩形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 是 $\text{[math]}$ 上的一点，连接 $\text{[math]}$ ， $\text{[math]}$ ，且 $\text{[math]}$ ，则 $\text{[math]}$ 的值为；

（3）如图3，在四边形 $\text{[math]}$ 中， $\text{[math]}$ ，点 $\text{[math]}$ 为 $\text{[math]}$ 上一点，连接 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 的垂线交 $\text{[math]}$ 的延长线于点 $\text{[math]}$ ，交 $\text{[math]}$ 的延长线于点 $\text{[math]}$ ，求证： $\text{[math]}$ ；

（4）如图4，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，将 $\text{[math]}$ 沿 $\text{[math]}$ 翻折，点 $\text{[math]}$ 落在点 $\text{[math]}$ 处得 $\text{[math]}$ ，点 $\text{[math]}$ ， $\text{[math]}$ 分别在边 $\text{[math]}$ ， $\text{[math]}$ 上，连接 $\text{[math]}$ ， $\text{[math]}$ ，且 $\text{[math]}$ .

①求 $\text{[math]}$ 的值；

②连接 $\text{[math]}$ ，若 $\text{[math]}$ ，直接写出 $\text{[math]}$ 的长度.

查看解析收藏纠错

+选题
17. 如图，在平面直角坐标系中，抛物线 $\text{[math]}$ 交 $\text{[math]}$ 轴于点 $\text{[math]}$ 和 $\text{[math]}$ ，交 $\text{[math]}$ 轴于点 $\text{[math]}$ ，抛物线的对称轴交 $\text{[math]}$ 轴于点 $\text{[math]}$ ，交抛物线于点 $\text{[math]}$ .

（1）求抛物线的解析式；

（2）将线段 $\text{[math]}$ 绕着点 $\text{[math]}$ 沿顺时针方向旋转得到线段 $\text{[math]}$ ，旋转角为 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的最小值.

（3） $\text{[math]}$ 为平面直角坐标系中一点，在抛物线上是否存在一点 $\text{[math]}$ ，使得以 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 为顶点的四边形为矩形？若存在，请直接写出点 $\text{[math]}$ 的横坐标；若不存在，请说明理由；

查看解析收藏纠错

+选题
18. 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 相交于点 $\text{[math]}$ ，与 $\text{[math]}$ 相交于点 $\text{[math]}$ ，连接 $\text{[math]}$ ，已知 $\text{[math]}$ .

（1）求证： $\text{[math]}$ 为 $\text{[math]}$ 的切线；

（2）若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长.

查看解析收藏纠错

+选题
19. 如图，在平面直角坐标系中，四边形 $\text{[math]}$ 为正方形，点 $\text{[math]}$ ， $\text{[math]}$ 在 $\text{[math]}$ 轴上，抛物线 $\text{[math]}$ 经过点 $\text{[math]}$ ， $\text{[math]}$ 两点，且与直线 $\text{[math]}$ 交于另一点 $\text{[math]}$ .

（1）求抛物线的解析式；

（2） $\text{[math]}$ 为抛物线对称轴上一点， $\text{[math]}$ 为平面直角坐标系中的一点，是否存在以点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 为顶点的四边形是以 $\text{[math]}$ 为边的菱形.若存在，请求出点 $\text{[math]}$ 的坐标；若不存在，请说明理由；

（3） $\text{[math]}$ 为 $\text{[math]}$ 轴上一点，过点 $\text{[math]}$ 作抛物线对称轴的垂线，垂足为 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ .探究 $\text{[math]}$ 是否存在最小值.若存在，请求出这个最小值及点 $\text{[math]}$ 的坐标；若不存在，请说明理由.

查看解析收藏纠错

+选题
20. 如图，在等腰直角三角形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，边长为2的正方形 $\text{[math]}$ 的对角线交点与点 $\text{[math]}$ 重合，连接 $\text{[math]}$ ， $\text{[math]}$ .

（1）求证： $\text{[math]}$ ；

（2）当点 $\text{[math]}$ 在 $\text{[math]}$ 内部，且 $\text{[math]}$ 时，设 $\text{[math]}$ 与 $\text{[math]}$ 相交于点 $\text{[math]}$ ，求 $\text{[math]}$ 的长；

（3）将正方形 $\text{[math]}$ 绕点 $\text{[math]}$ 旋转一周，当点 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 三点在同一直线上时，请直接写出 $\text{[math]}$ 的长.

查看解析收藏纠错

+选题
21. 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 为 $\text{[math]}$ 的中点，连接 $\text{[math]}$ ，将线段 $\text{[math]}$ 绕点 $\text{[math]}$ 顺时针旋转 $\text{[math]}$ 得到线段 $\text{[math]}$ ，且 $\text{[math]}$ 交线段 $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ 的平分线 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ .

（1）如图1，若 $\text{[math]}$ ，则线段 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系是， $\text{[math]}$ ；

（2）如图2，在（1）的条件下，过点 $\text{[math]}$ 作 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ .
①试判断四边形 $\text{[math]}$ 的形状，并说明理由；

②求证： $\text{[math]}$ ；

（3）如图3，若 $\text{[math]}$ ， $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ，请直接写出 $\text{[math]}$ 的值（用含 $\text{[math]}$ 的式子表示）.

查看解析收藏纠错

+选题
22. 如图，BD是半径为3的⊙O的一条弦，BD＝4 $\text{[math]}$ ，点A是⊙O上的一个动点（不与点B，D重合），以A，B，D为顶点作▱ABCD.

（1）如图2，若点A是劣弧 $\text{[math]}$ 的中点.
①求证：▱ABCD是菱形；

②求▱ABCD的面积.

（2）若点A运动到优弧 $\text{[math]}$ 上，且▱ABCD有一边与⊙O相切.
①求AB的长；

②直接写出▱ABCD对角线所夹锐角的正切值.

查看解析收藏纠错

+选题
23. 如图，锐角三角形ABC内接于⊙O，∠BAC的平分线AG交⊙O于点G，交BC边于点F，连结BG。

（1）求证：△ABG∽△AFC；

（2）已知AB= $\text{[math]}$ ，AC=AF= $\text{[math]}$ ，求线段FG的长（用含 $\text{[math]}$ ， $\text{[math]}$ 的代数式表示）；

（3）已知点E在线段AF上（不与点A，点F重合），点D在线段AE上（不与点A，点E重合），∠ABD=∠CBE，求证： $\text{[math]}$ 。

查看解析收藏纠错

+选题
24. 如图，在平面直角坐标系中， $\text{[math]}$ 经过原点 $\text{[math]}$ ，分别交 $\text{[math]}$ 轴、 $\text{[math]}$ 轴于 $\text{[math]}$ ， $\text{[math]}$ ，连结 $\text{[math]}$ .直线 $\text{[math]}$ 分别交 $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ （点 $\text{[math]}$ 在左侧），交 $\text{[math]}$ 轴于点 $\text{[math]}$ ，连结 $\text{[math]}$ .

（1）求 $\text{[math]}$ 的半径和直线 $\text{[math]}$ 的函数表达式.

（2）求点 $\text{[math]}$ ， $\text{[math]}$ 的坐标.

（3）点 $\text{[math]}$ 在线段 $\text{[math]}$ 上，连结 $\text{[math]}$ .当 $\text{[math]}$ 与 $\text{[math]}$ 的一个内角相等时，求所有满足条件的 $\text{[math]}$ 的长.

查看解析收藏纠错

+选题
25. 如图，矩形ABCD中， $\text{[math]}$ ，点E是边AD的中点，点F是对角线BD上一动点， $\text{[math]}$ .连结EF，作点D关于直线EF的对称点P.

（1）若 $\text{[math]}$ ，求DF的长.

（2）若 $\text{[math]}$ ，求DF的长.

（3）直线PE交BD于点Q，若 $\text{[math]}$ 是锐角三角形，求DF长的取值范围.

查看解析收藏纠错

+选题
26. 如图1，四边形 $\text{[math]}$ 内接于 $\text{[math]}$ ， $\text{[math]}$ 为直径， $\text{[math]}$ 上存在点E，满足 $\text{[math]}$ ，连结 $\text{[math]}$ 并延长交 $\text{[math]}$ 的延长线于点F， $\text{[math]}$ 与 $\text{[math]}$ 交于点G.

（1）若 $\text{[math]}$ ，请用含 $\text{[math]}$ 的代数式表列 $\text{[math]}$ .

（2）如图2，连结 $\text{[math]}$ .求证； $\text{[math]}$ .

（3）如图3，在（2）的条件下，连结 $\text{[math]}$ ， $\text{[math]}$ .
①若 $\text{[math]}$ ，求 $\text{[math]}$ 的周长.

②求 $\text{[math]}$ 的最小值.

查看解析收藏纠错

+选题
27. 在平面直角坐标系中，点A的坐标为 $\text{[math]}$ ，点B在直线 $\text{[math]}$ 上，过点B作AB的垂线，过原点O作直线l的垂线，两垂线相交于点C.

（1）如图，点B，C分别在第三、二象限内，BC与AO相交于点D.
①若 $\text{[math]}$ ，求证： $\text{[math]}$ .

②若 $\text{[math]}$ ，求四边形 $\text{[math]}$ 的面积.

（2）是否存在点B，使得以 $\text{[math]}$ 为顶点的三角形与 $\text{[math]}$ 相似？若存在，求OB的长；若不存在，请说明理由.

查看解析收藏纠错

+选题
28. 如图，在平面直角坐标系中，抛物线 $\text{[math]}$ 与坐标轴交于 $\text{[math]}$ 两点，直线 $\text{[math]}$ 交 $\text{[math]}$ 轴于点 $\text{[math]}$ .点 $\text{[math]}$ 为直线 $\text{[math]}$ 下方抛物线上一动点，过点 $\text{[math]}$ 作 $\text{[math]}$ 轴的垂线，垂足为 $\text{[math]}$ 分别交直线 $\text{[math]}$ 于点 $\text{[math]}$ .

（1）求抛物线 $\text{[math]}$ 的表达式；

（2）当 $\text{[math]}$ ，连接 $\text{[math]}$ ，求 $\text{[math]}$ 的面积；

（3） ① $\text{[math]}$ 是 $\text{[math]}$ 轴上一点，当四边形 $\text{[math]}$ 是矩形时，求点 $\text{[math]}$ 的坐标；
②在①的条件下，第一象限有一动点 $\text{[math]}$ ，满足 $\text{[math]}$ ，求 $\text{[math]}$ 周长的最小值.

查看解析收藏纠错

+选题
29. 探究：是否存在一个新矩形，使其周长和面积为原矩形的2倍、 $\text{[math]}$ 倍、k倍．

（1）若该矩形为正方形，是否存在一个正方形，使其周长和面积都为边长为2的正方形的2倍？（填“存在”或“不存在”）．

（2）继续探究，是否存在一个矩形，使其周长和面积都为长为3，宽为2的矩形的2倍？
同学们有以下思路：

①设新矩形长和宽为x、y ，则依题意 $\text{[math]}$ ， $\text{[math]}$ ，

联立 $\text{[math]}$ 得 $\text{[math]}$ ，再探究根的情况：

根据此方法，请你探究是否存在一个矩形，使其周长和面积都为原矩形的 $\text{[math]}$ 倍；

②如图也可用反比例函数与一次函数证明 $\text{[math]}$ ： $\text{[math]}$ ， $\text{[math]}$ ： $\text{[math]}$ ，那么，

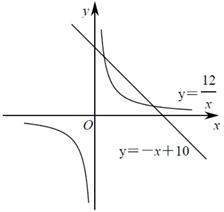
a ．是否存在一个新矩形为原矩形周长和面积的2倍？

b ．请探究是否有一新矩形周长和面积为原矩形的 $\text{[math]}$ ，若存在，用图像表达；

c ．请直接写出当结论成立时k的取值范围：．

查看解析收藏纠错

+选题
30. 在正方形 $\text{[math]}$ 中，等腰直角 $\text{[math]}$ ， $\text{[math]}$ ，连接 $\text{[math]}$ ，H为 $\text{[math]}$ 中点，连接 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ ，发现 $\text{[math]}$ 和 $\text{[math]}$ 为定值.

（1） ① $\text{[math]}$ ▲ ；
② $\text{[math]}$ ▲ .

③小明为了证明①②，连接 $\text{[math]}$ 交 $\text{[math]}$ 于O ，连接 $\text{[math]}$ ，证明了 $\text{[math]}$ 和 $\text{[math]}$ 的关系，请你按他的思路证明①②.

（2）小明又用三个相似三角形（两个大三角形全等）摆出如图2， $\text{[math]}$ ， $\text{[math]}$ （ $\text{[math]}$ ）
求① $\text{[math]}$ （用k的代数式表示）

② $\text{[math]}$ （用k、 $\text{[math]}$ 的代数式表示）

查看解析收藏纠错

+选题
31. 在矩形 $\text{[math]}$ 中， $\text{[math]}$ ，点 $\text{[math]}$ ， $\text{[math]}$ 分别是边 $\text{[math]}$ 、 $\text{[math]}$ 上的动点，且 $\text{[math]}$ ，连接 $\text{[math]}$ ，将矩形 $\text{[math]}$ 沿 $\text{[math]}$ 折叠，点 $\text{[math]}$ 落在点 $\text{[math]}$ 处，点 $\text{[math]}$ 落在点 $\text{[math]}$ 处．

（1）如图1，当 $\text{[math]}$ 与线段 $\text{[math]}$ 交于点 $\text{[math]}$ 时，求证： $\text{[math]}$ ；

（2）如图2，当点 $\text{[math]}$ 在线段 $\text{[math]}$ 的延长线上时， $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，求证：点 $\text{[math]}$ 在线段 $\text{[math]}$ 的垂直平分线上；

（3）当 $\text{[math]}$ 时，在点 $\text{[math]}$ 由点 $\text{[math]}$ 移动到 $\text{[math]}$ 中点的过程中，计算出点 $\text{[math]}$ 运动的路线长．

查看解析收藏纠错

+选题
32. 在一平面内，线段 $\text{[math]}$ ，线段 $\text{[math]}$ ，将这四条线段顺次首尾相接．把 $\text{[math]}$ 固定，让 $\text{[math]}$ 绕点 $\text{[math]}$ 从 $\text{[math]}$ 开始逆时针旋转角 $\text{[math]}$ 到某一位置时， $\text{[math]}$ ， $\text{[math]}$ 将会跟随出现到相应的位置．

（1）论证如图1，当 $\text{[math]}$ 时，设 $\text{[math]}$ 与 $\text{[math]}$ 交于点 $\text{[math]}$ ，求证： $\text{[math]}$ ；

（2）发现当旋转角 $\text{[math]}$ 时， $\text{[math]}$ 的度数可能是多少？

（3）尝试取线段 $\text{[math]}$ 的中点 $\text{[math]}$ ，当点 $\text{[math]}$ 与点 $\text{[math]}$ 距离最大时，求点 $\text{[math]}$ 到 $\text{[math]}$ 的距离；

（4）拓展 ①如图2，设点 $\text{[math]}$ 与 $\text{[math]}$ 的距离为 $\text{[math]}$ ，若 $\text{[math]}$ 的平分线所在直线交 $\text{[math]}$ 于点 $\text{[math]}$ ，直接写出 $\text{[math]}$ 的长（用含 $\text{[math]}$ 的式子表示）；
②当点 $\text{[math]}$ 在 $\text{[math]}$ 下方，且 $\text{[math]}$ 与 $\text{[math]}$ 垂直时，直接写出 $\text{[math]}$ 的余弦值．

查看解析收藏纠错

+选题
33. 如图1，O为半圆的圆心，C、D为半圆上的两点，且 $\text{[math]}$ ．连接AC并延长，与BD的延长线相交于点E ．

（1）求证：CD＝ED；

（2） AD与OC ， BC分别交于点F ， H ．
①若CF＝CH ，如图2，求证：CF•AF＝FO•AH；

②若圆的半径为2，BD＝1，如图3，求AC的值．

查看解析收藏纠错

+选题
34. 二次函数y＝ax²+bx+4（a≠0）的图象经过点A（﹣4，0），B（1，0），与y轴交于点C ，点P为第二象限内抛物线上一点，连接BP、AC ，交于点Q ，过点P作PD⊥x轴于点D ．

（1）求二次函数的表达式；

（2）连接BC ，当∠DPB＝2∠BCO时，求直线BP的表达式；

（3）请判断： $\text{[math]}$ 是否有最大值，如有请求出有最大值时点P的坐标，如没有请说明理由．

查看解析收藏纠错

+选题
35. 如图1，在四边形ABCD中，∠ABC=∠BCD，点E在边BC上，且AE∥CD，DE∥AB，CF∥AD交线段AE于点F，连接BF.

（1）求证：△ABF≌△EAD；

（2）如图2，若AB=9，CD=5，∠ECF＝∠AED，求BE的长；

（3）如图3，若BF的延长线经过AD的中点M，求 $\text{[math]}$ 的值.

查看解析收藏纠错

+选题
36. 已知在平面直角坐标系xOy中，点A是反比例函数 $\text{[math]}$ 图像上的一个动点，连结AO，AO的延长线交反比例函数 $\text{[math]}$ （ $\text{[math]}$ ， $\text{[math]}$ ）的图像于点B，过点A作AE⊥ $\text{[math]}$ 轴于点E。

（1）如图1，过点B作BF⊥ $\text{[math]}$ 轴于点F，连结EF，
①若 $\text{[math]}$ ，求证：四边形AEFO是平行四边形；

②连结BE，若 $\text{[math]}$ ，求△BOE的面积。

（2）如图2，过点E作EP∥AB，交反比例函数 $\text{[math]}$ （ $\text{[math]}$ ， $\text{[math]}$ ）的图像于点P，连结OP。
试探究：对于确定的实数 $\text{[math]}$ ，动点A在运动过程中，△POE的面积是否会发生变化？请说明理由。

查看解析收藏纠错

+选题
37. 我们知道：如图①，点 $\text{[math]}$ 把线段 $\text{[math]}$ 分成两部分，如果 $\text{[math]}$ .那么称点 $\text{[math]}$ 为线段 $\text{[math]}$ 的黄金分割点.它们的比值为 $\text{[math]}$ .

（1）在图①中，若 $\text{[math]}$ ，则 $\text{[math]}$ 的长为 $\text{[math]}$ ；

（2）如图②，用边长为 $\text{[math]}$ 的正方形纸片进行如下操作：对折正方形 $\text{[math]}$ 得折痕 $\text{[math]}$ ，连接 $\text{[math]}$ ，将 $\text{[math]}$ 折叠到 $\text{[math]}$ 上，点 $\text{[math]}$ 对应点 $\text{[math]}$ ，得折痕 $\text{[math]}$ .试说明 $\text{[math]}$ 是 $\text{[math]}$ 的黄金分割点；

（3）如图③，小明进一步探究：在边长为 $\text{[math]}$ 的正方形 $\text{[math]}$ 的边 $\text{[math]}$ 上任取点 $\text{[math]}$ $\text{[math]}$ ，连接 $\text{[math]}$ ，作 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ ，延长 $\text{[math]}$ 、 $\text{[math]}$ 交于点 $\text{[math]}$ .他发现当 $\text{[math]}$ 与 $\text{[math]}$ 满足某种关系时 $\text{[math]}$ 、 $\text{[math]}$ 恰好分别是 $\text{[math]}$ 、 $\text{[math]}$ 的黄金分割点.请猜想小明的发现，并说明理由.

查看解析收藏纠错

+选题
38. 如图，四边形 $\text{[math]}$ 是正方形，点 $\text{[math]}$ 是射线 $\text{[math]}$ 上的动点，连接 $\text{[math]}$ ，以 $\text{[math]}$ 为对角线作正方形 $\text{[math]}$ （ $\text{[math]}$ 按逆时针排列），连接 $\text{[math]}$ .

（1）当点 $\text{[math]}$ 在线段 $\text{[math]}$ 上时.
①求证： $\text{[math]}$ ；

②求证： $\text{[math]}$ ；

（2）设正方形 $\text{[math]}$ 的面积为 $\text{[math]}$ ，正方形 $\text{[math]}$ 的面积为 $\text{[math]}$ ，以 $\text{[math]}$ 为原点的四边形的面积为 $\text{[math]}$ ，当 $\text{[math]}$ 时，请直接写出 $\text{[math]}$ 的值.

查看解析收藏纠错

+选题
39. 如图1 ，直线 $\text{[math]}$ 与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ，与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ，抛物线 $\text{[math]}$ 经过点 $\text{[math]}$ 和点 $\text{[math]}$ 从点，开始沿射线 $\text{[math]}$ 方向以每秒 $\text{[math]}$ 个单位长度的速度平移，平移后的三角形记为 $\text{[math]}$ （点 $\text{[math]}$ 的对应点分别为点 $\text{[math]}$ ），平移时间为 $\text{[math]}$ 秒，射线 $\text{[math]}$ 交 $\text{[math]}$ 轴于点 $\text{[math]}$ ，交抛物线于点 $\text{[math]}$ ，连接 $\text{[math]}$ .

（1）求抛物线的解析式；

（2）当 $\text{[math]}$ 时，请直接写出 $\text{[math]}$ 的值；

（3）如图2，点 $\text{[math]}$ 在抛物线上，点 $\text{[math]}$ 的横坐标是点 $\text{[math]}$ 的横坐标的 $\text{[math]}$ ，连接 $\text{[math]}$ 与 $\text{[math]}$ 相交于点 $\text{[math]}$ ，当 $\text{[math]}$ 时，求 $\text{[math]}$ 的值.

查看解析收藏纠错

+选题
40. 已知：菱形 $\text{[math]}$ 和菱形 $\text{[math]}$ ， $\text{[math]}$ ，起始位置点 $\text{[math]}$ 在边 $\text{[math]}$ 上，点 $\text{[math]}$ 在 $\text{[math]}$ 所在直线上，点 $\text{[math]}$ 在点 $\text{[math]}$ 的右侧，点 $\text{[math]}$ 在点 $\text{[math]}$ 的右侧，连接 $\text{[math]}$ 和 $\text{[math]}$ ，将菱形 $\text{[math]}$ 以 $\text{[math]}$ 为旋转中心逆时针旋转 $\text{[math]}$ 角（ $\text{[math]}$ ）.

（1）如图1，若点 $\text{[math]}$ 与 $\text{[math]}$ 重合，且 $\text{[math]}$ ，求证： $\text{[math]}$ ；

（2）若点 $\text{[math]}$ 与 $\text{[math]}$ 不重合， $\text{[math]}$ 是 $\text{[math]}$ 上一点，当 $\text{[math]}$ 时，连接 $\text{[math]}$ 和 $\text{[math]}$ ， $\text{[math]}$ 和 $\text{[math]}$ 所在直线相交于点 $\text{[math]}$ ；
①如图2，当 $\text{[math]}$ 时，请猜想线段 $\text{[math]}$ 和线段 $\text{[math]}$ 的数量关系及 $\text{[math]}$ 的度数；

②如图3，当 $\text{[math]}$ 时，请求出线段 $\text{[math]}$ 和线段 $\text{[math]}$ 的数量关系及 $\text{[math]}$ 的度数；

③在②的条件下，若点 $\text{[math]}$ 与 $\text{[math]}$ 的中点重合， $\text{[math]}$ ， $\text{[math]}$ ，在整个旋转过程中，当点 $\text{[math]}$ 与点 $\text{[math]}$ 重合时，请直接写出线段 $\text{[math]}$ 的长.

查看解析收藏纠错

+选题

全国历年中考数学真题精选汇编：图形变换与视图2

一、单选题

二、填空题

三、解答题

四、综合题

相关试卷 收起∨

相关试卷收起∨