修改时间:2021-11-16 浏览次数:150 类型:复习试卷
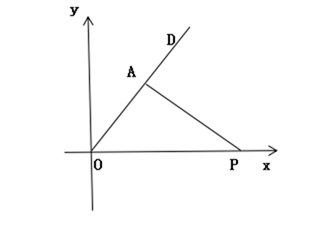


我们知道,可以用一个数表示数轴上的一个点,而每个数在数轴上也有一个点与之对应。现在把这个数轴叫做x轴,同时,增加一个垂直于x轴的数轴,叫做y轴,如下图。这样,我们可以用一组数对来表示平面上的一个点,同时,平面上的一个点也可以用一组数对来表示,比如下图中A点的位置可以表示为(2,3),而数对(2,3)所对应的点即为A。若平面上的点M ,N
,我们定义点M、N在x轴方向上的距离为:
,点M、N在y轴方向上的距离为:
。例如,点G(3,4)与点H(1,-1)在x轴方向上的距离为:|3-1|=2,点M、N在y轴方向上的距离为:|4-(-1)|=5。

四边形DEFG的四个顶点的坐标分别为:D(1,2),E(3,2),F(3,4),G(1,4).将四边形DEFG经过“n倍变换”得到四边形D1E1F1G1.当两个四边形重叠部分的面积大于0时,直接写出n的取值范围.
平移到 称为将点
进行“
型平移”,点
称为将点
进行“
型平移”的对应点;将图形
上的所有点进行“
型平移”称为将图形
进行“
型平移”.例如,将点
平移
称为将点
进行“
型平移”,将点
平移到
称为将点
进行“
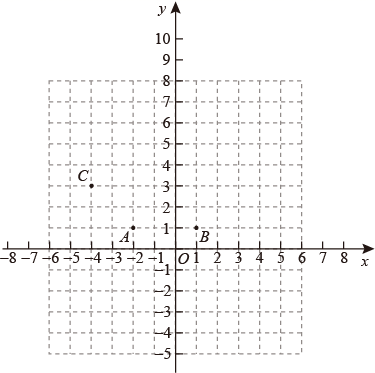
型平移”.已知点
,
.


(温馨提示:三角形的面积= ×底×高).
试题篮