2024年浙教版数学八（下）微素养核心突破25 反比例函数与几何综合

1. 如图，在平面直角坐标系中，菱形ABCD的顶点C与原点O重合，点B在y轴的正半轴上，点A在反比例函数y= $\text{[math]}$ (x>0)的图象上，点D的坐标为(4，3)．

（1）求k的值．

（2）若将菱形ABCD沿x轴正方向平移m个单位．
①当菱形的顶点B落在反比例函数的图象上时，求m的值；
②在平移过程中，若反比例函数图象与菱形的边AD始终有交点，求m的取值范围．

查看解析收藏纠错

+选题
2. 阅读理解：
在平面直角坐标系中，点M的坐标为(x₁ ， y₁)，点N的坐标为(x₂ ， y₂)，且x₁≠x₂ ， y₁≠y₂ ，若M，N为某矩形的两个顶点，且该矩形的边均与某条坐标轴垂直，则称该矩形为M，N的“相关矩形”．如图中的矩形为点M，N的“相关矩形”。

（1）已知点A的坐标为(2，0)．
①若点B的坐标为(4，4)，则点A，B的“相关矩形”的周长为；
②若点C在直线x=4上，且点A，C的“相关矩形”为正方形，求直线AC的表达式．

（2）已知点P的坐标为(3，-4)，点Q的坐标为(6，-2)，若使函数y= $\text{[math]}$ 的图象与点P，Q的“相关矩形”有两个公共点，直接写出k的取值范围．

查看解析收藏纠错

+选题

3. 如图，正比例函数y₁= $\text{[math]}$ x和反比例函数y₂= $\text{[math]}$ (x>0)的图象交于点A(m，2)．

（1）求反比例函数的表达式；

（2）将直线OA向上平移3个单位后，与y轴交于点B，与y₂= $\text{[math]}$ (x>0)的图象交于点C，连结AB，AC，求△ABC的面积

查看解析收藏纠错

+选题
4. 如图，一次函数 $\text{[math]}$ 的图象与反比例函数 $\text{[math]}$ 的图象交于点 $\text{[math]}$ ，与x轴交于点B，与y轴交于点 $\text{[math]}$ ．

（1）求m的值和一次函数的表达式；

（2）已知P为反比例函数 $\text{[math]}$ 图象上的一点， $\text{[math]}$ ，求点P的坐标．

查看解析收藏纠错

+选题
5. 如图，一次函数y=kx+ $\text{[math]}$ (k为常数，k≠0)的图象与反比例函数y= $\text{[math]}$ (m为常数，m≠0)的图象在第一象限交于点A(1，n)，与x轴交于点B(-3，0)．

（1）求一次函数和反比例函数的表达式；

（2）点P在x轴上，△ABP是以AB为腰的等腰三角形，请直接写出点P的坐标．

查看解析收藏纠错

+选题
6. 如图，直线y₁=x+b交x轴于点B，交y轴于点A(0，2) ，与反比例函数y₂= $\text{[math]}$ 的图象交于C(1，m)，D(n，-1)两点，连结OC，OD．

（1）求k的值；

（2）点M是反比例函数y₂= $\text{[math]}$ 上一点，是否存在点M，使以点M，C，D为顶点的三角形是直角三角形，且CD为直角边，若存在，请写出点M的坐标；若不存在，请说明理由．(提示：两直线垂直，斜率乘积为-1)

查看解析收藏纠错

+选题
7. 如图，过点C(1，0)作两条直线，分别交函数y= $\text{[math]}$ (x>0)，y= $\text{[math]}$ (x<0)的图象于A，B两点，连结AB．若AB∥x轴，则△ABC的面积是（）

A . 2 B . 3 C . 4 D . 6

查看解析收藏纠错

+选题
8. 如图，在平面直角坐标系中，反比例函数 $\text{[math]}$ 的图象经过 $\text{[math]}$ 的顶点 $\text{[math]}$ .若 $\text{[math]}$ 轴，点 $\text{[math]}$ 的坐标为 $\text{[math]}$ 的面积为3，5，则 $\text{[math]}$ 的值为（）

A . 6.5 B . 7 C . 13 D . 14

查看解析收藏纠错

+选题
9. 如图，点A是反比例函数 $\text{[math]}$ 的图象上的一点，过点A作AB⊥x轴，垂足为B．点C为y轴上的一点，连接AC，BC．若△ABC的面积为3，则k的值是（　　）

A . 3 B . -6 C . 6 D . -3

查看解析收藏纠错

+选题
10. 如图，已知动点P在反比例函数 $\text{[math]}$ 的图象上， $\text{[math]}$ 轴于点A，动点B在y轴正半轴上，当点A的横坐标逐渐变小时， $\text{[math]}$ 的面积将会（）

A . 越来越小 B . 越来越大 C . 不变 D . 先变大后变小

查看解析收藏纠错

+选题
11. 如图，点 $\text{[math]}$ 是反比例函数 $\text{[math]}$ 的图象上的一点，过点 $\text{[math]}$ 作 $\text{[math]}$ 轴，垂足为 $\text{[math]}$ 点 $\text{[math]}$ 为 $\text{[math]}$ 轴上的一点，连接 $\text{[math]}$ ， $\text{[math]}$ 若 $\text{[math]}$ 的面积为 $\text{[math]}$ ，则 $\text{[math]}$ 的值是（）

A . 3 B . -6 C . 6 D . -3

查看解析收藏纠错

+选题
12. 如图， $\text{[math]}$ 是反比例函数 $\text{[math]}$ 图象上的一点， $\text{[math]}$ 轴于点 $\text{[math]}$ ．若 $\text{[math]}$ 的面积是3，则 $\text{[math]}$ 的值是.

查看解析收藏纠错

+选题
13. 把一个含60°角的三角尺ABC按如图所示的方式摆放在平面直角坐标系中，其中60°角的顶点 B 在x轴上，斜边AB与x轴的夹角∠ABO=60°.若BC=2，点A，C同时落在一个反比例函数的图象上，则点 B的坐标为.

查看解析收藏纠错

+选题

14. 如图，已知直线l：y=x+4与反比例函数y= $\text{[math]}$ (x<0)的图象交于点A(-1，n)，直线I'经过点A，且与l关于直线x=-1对称．

（1）求反比例函数的表达式；

（2）求图中阴影部分的面积

查看解析收藏纠错

+选题
15. 如图，在菱形OABC中，OC=8，∠AOC=60°，OA在x轴正半轴上，D是边OC上的一点(不与点O，C重合)，过点D作DE⊥AB于点E.若点D，E都在反比例函数 $\text{[math]}$ （k>0，k≠0)的图象上，则k的值为（）

A . 8 $\text{[math]}$ B . 9 C . 9 $\text{[math]}$ D . 16

查看解析收藏纠错

+选题
16. 如图，在反比例函数 $\text{[math]}$ 的图象上有点 P₁，P₂，P₃，它们的横坐标依次为1，3，6，分别过这些点作x轴与y轴的垂线段.若图中阴影部分的面积分别记为 S₁，S₂，且S₂=3，则 S₁的值为（）

A . 3 B . 4 C . 5 D . 6

查看解析收藏纠错

+选题
17. 如图，在平面直角坐标系中，菱形ABCD在第一象限内，边BC与x轴平行，A，B两点的纵坐标分别为6，4，反比例函数 $\text{[math]}$ 的图象经过A，B 两点.若菱形 ABCD的面积为2 $\text{[math]}$ ，则k 值为（）

A . 16 B . 12 C . 10 D . 9

查看解析收藏纠错

+选题
18. 如图，矩形 ABCD的顶点A，D在y轴上，顶点 $\text{[math]}$ 在第一象限，x轴为该矩形的一条对称轴.若反比例函数 $\text{[math]}$ 的图象经过点C，则矩形 ABCD的面积为（）

A . $\text{[math]}$ B . 2 C . 4 D . 8

查看解析收藏纠错

+选题
19. 如图，已知正方形 $\text{[math]}$ 的面积为9．它的两个顶点 $\text{[math]}$ ， $\text{[math]}$ 是反比例函数 $\text{[math]}$ （ $\text{[math]}$ ， $\text{[math]}$ ）的图象上两点，若点 $\text{[math]}$ 的坐标是 $\text{[math]}$ ，则 $\text{[math]}$ 的值为（）

A . 3 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
20. 如图，在平面直角坐标系中，正方形ABCD的顶点A，B分别在x轴、y轴上，对角线相交于点E，反比例函数= $\text{[math]}$ （x＞0，k＞0）的图象经过点C，E.若点 A(3，0)，则k的值为 .

查看解析收藏纠错

+选题
21. 如图，在平面直角坐标系中，正方形OABC的顶点O与坐标原点重合，点C的坐标为(0，3)，点A在x轴的负半轴上，点M，D分别在OA ，AB上，且AD=AM=2．一次函数y=kx+b的图象过点D和M，反比例函数y= $\text{[math]}$ 的图象经过点D，与BC交点为N．

（1）求反比例函数和一次函数的表达式；

（2）若点P在y轴上，且使四边形OMDP的面积与四边形OMNC的面积相等，求点P的坐标．

查看解析收藏纠错

+选题
22. 如图，在平面直角坐标系 $\text{[math]}$ 中，直线 $\text{[math]}$ 与 $\text{[math]}$ ， $\text{[math]}$ 轴分别相交于点A，B，与反比例函数 $\text{[math]}$ 的图象相交于点C，已知 $\text{[math]}$ ，点C的横坐标为2．

（1）求 $\text{[math]}$ ， $\text{[math]}$ 的值；

（2）平行于 $\text{[math]}$ 轴的动直线与 $\text{[math]}$ 和反比例函数的图象分别交于点D，E，若以B，D，E，O为顶点的四边形为平行四边形，求点D的坐标．

查看解析收藏纠错

+选题
23. 如图，四边形ABCD的四个顶点分别在反比例函数y= $\text{[math]}$ 与y= $\text{[math]}$ (x>0，0<m<n)的图象上，对角线BD∥y轴，且BD⊥AC于点P.已知点B的横坐标为4

（1）当m=4，n=20时
①若点P的纵坐标为2，求直线AB的函数表达式

②若点P是BD的中点，试判断四边形ABCD的形状，并说明理由

（2）四边形ABCD能否成为正方形?若能，求此时m，n之间的数量关系；若不能，试说明理由.

查看解析收藏纠错

+选题
24. 如图， ▱ OABC的顶点O 是坐标原点，点 A 在x 轴的正半轴上，点 B，C在第一象限，反比例函数 $\text{[math]}$ ， y=kx(k≠0)的图象分别经过点 C，B.若 OC=AC，则k的值为.

查看解析收藏纠错

+选题
25. 如图，在平面直角坐标系中，□CODE的顶点C 在x轴的负半轴上，点D，E在第二象限，点E的纵坐标为2，反比例函数 $\text{[math]}$ 的图象与OD 相交于点A(a，b).若点 B的坐标为 $\text{[math]}$ 且点B 在∠ODE的边上，则 OB 的长.为.

查看解析收藏纠错

+选题
26. 如图，一次函数y=mx+1的图象与反比例函数y= $\text{[math]}$ 的图象相交于A、B两点，点C在x轴正半轴上，点D(1，-2)，连接OA、OD、DC、AC ，四边形OACD为菱形．

（1）求一次函数与反比例函数的解析式；

（2）根据图象，直接写出反比例函数的值小于2时，x的取值范围；

（3）设点P是直线AB上一动点，且S_△OAP= $\text{[math]}$ S_菱形OACD ，求点P的坐标．

查看解析收藏纠错

+选题

27. 如图，直线y=kx+2与双曲线y= $\text{[math]}$ 相交于点A，B，已知点A的横坐标为1．

（1）求直线y=kx+2的表达式及点B的坐标；

（2）以线段AB为斜边在直线AB的上方作等腰直角三角形ABC．求经过点C的双曲线的表达式

查看解析收藏纠错

+选题
28. 已知直线y=x与反比例函数y= $\text{[math]}$ 的图象在第一象限交于点M(2，a)．

（1）求反比例函数的表达式；

（2）如图，将直线y=x向上平移b个单位后与y= $\text{[math]}$ 的图象交于点A(1，m)和点B(n，-1)，求b的值；

（3）在(2)的条件下，设直线AB与x轴、y轴分别交于点C，D，求证：△AOD≌△BOC．

查看解析收藏纠错

+选题
29. 如图，已知点A是反比例函数 $\text{[math]}$ 的图象上的一个动点，连接OA，若将线段OA绕点O顺时针旋转90°得到线段OB，则点B所在图象的反比例函数表达式为.

查看解析收藏纠错

+选题
30. 如图，在平面直角坐标系中，一次函数y=-4x+4 的图象与 x轴、y轴分别相交于点A，B.正方形ABCD 的顶点C，D位于第一象限，其中顶点 D 位于反比例函.数 $\text{[math]}$ 的图象上.若将正方形ABCD 向左平移n个单位后，顶点C恰好落在该反比例函数的图象上，则 n的值是.
.

查看解析收藏纠错

+选题
31. 如图1，四边形 $\text{[math]}$ 为正方形，点 $\text{[math]}$ 在 $\text{[math]}$ 轴上，点 $\text{[math]}$ 在 $\text{[math]}$ 轴上，且 $\text{[math]}$ ，反比例函数 $\text{[math]}$ 在第一象限的图象经过正方形的顶点 $\text{[math]}$ ．

（1）求点 $\text{[math]}$ 的坐标；

（2）如图2，将正方形 $\text{[math]}$ 沿 $\text{[math]}$ 轴向右平移得到正方形 $\text{[math]}$ ，点 $\text{[math]}$ 恰好落在反比例函数的图象上，求此时点 $\text{[math]}$ 的坐标；

（3）在(2)的条件下，点 $\text{[math]}$ 为 $\text{[math]}$ 轴上一动点，平面内是否存在点 $\text{[math]}$ ，使以点 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 为顶点的四边形为菱形，若存在，请直接写出点 $\text{[math]}$ 的坐标，若不存在，请说明理由．

查看解析收藏纠错

+选题
32. （性质认识）
如图，在函数 $\text{[math]}$ 的图象上任取两点 $\text{[math]}$ 、 $\text{[math]}$ 向坐标轴作垂直，连接垂足 $\text{[math]}$ 、 $\text{[math]}$ 或 $\text{[math]}$ 、 $\text{[math]}$ ，则一定有如下结论： $\text{[math]}$ ， $\text{[math]}$ .

（1）（数学理解）如图①，借助（性质认知）的结论，猜想 $\text{[math]}$ $\text{[math]}$ （填“>”、“=”或“<”）；

（2）如图②，借助（性质认知）的结论，证明： $\text{[math]}$ ；

（3）（问题解决）如图③，函数 $\text{[math]}$ 的图象与过原点的直线相交于 $\text{[math]}$ 、 $\text{[math]}$ 两点，点 $\text{[math]}$ 是第一象限内图象上的动点（点 $\text{[math]}$ 在点 $\text{[math]}$ 的左侧），直线 $\text{[math]}$ 分别交于 $\text{[math]}$ 轴、 $\text{[math]}$ 轴于点 $\text{[math]}$ 、 $\text{[math]}$ ，连接 $\text{[math]}$ 分别交 $\text{[math]}$ 轴、 $\text{[math]}$ 轴于点 $\text{[math]}$ 、 $\text{[math]}$ .请证明： $\text{[math]}$ .

（4）在第（3）问中，若 $\text{[math]}$ ，则 $\text{[math]}$ .

查看解析收藏纠错

+选题
33. 在直角坐标系中，反比例函数 $\text{[math]}$ ，过点 $\text{[math]}$ .

（1）求 $\text{[math]}$ 关于 $\text{[math]}$ 的函数表达式.

（2）求当 $\text{[math]}$ 时，自变量 $\text{[math]}$ 的取值范围.

（3）在 $\text{[math]}$ 轴上有一点 $\text{[math]}$ ，在反比例函数图象上有一个动点 $\text{[math]}$ ，以 $\text{[math]}$ 为一边作一个正方形 $\text{[math]}$ ，当正方形 $\text{[math]}$ 有两个顶点在坐标轴上时，画出状态图并求出相应 $\text{[math]}$ 点坐标.

查看解析收藏纠错

+选题
34. 如图1，在平面直角坐标系中，反比例函数y= $\text{[math]}$ (k>0，k为常数，x>0)的图象经过正方形ABCO的顶点B，点A的坐标是(0，1).点D在线段OA上，点E在射线OC上，以BD，DE为边的平行四边形BDEF的顶点F恰好在该反比例函数的图象上

（1）求k的值：

（2）若点D的坐标是(0， $\text{[math]}$ )，求点E的坐标：

（3）如图2，当点E在OC的延长线上时，连结BE若BD⊥BE，BD=BE.求点D的坐标.

查看解析收藏纠错

+选题

35. 如图， $\text{[math]}$ ， $\text{[math]}$ 是反比例函数 $\text{[math]}$ 的图象上的两点，点P是反比例函数 $\text{[math]}$ 的图象位于线段 $\text{[math]}$ 下方的一动点，过点P作 $\text{[math]}$ 轴于M，交线段 $\text{[math]}$ 于Q．设点M横坐标为x，则 $\text{[math]}$ 面积的最大值为，此时 $\text{[math]}$ ．

查看解析收藏纠错

+选题
36. 如图，一次函数y＝2x与反比例函数y＝ $\text{[math]}$ （k＞0）的图象交于点A ， B两点，点C在x轴上运动，连接AC ，点Q为AC中点，若点C运动过程中，OQ的最小值为1，则点B的坐标为．

查看解析收藏纠错

+选题
37.
如图，点A（a，1）、B（﹣1，b）都在双曲线y=﹣ $\text{[math]}$ 上，点P、Q分别是x轴、y轴上的动点，当四边形PABQ的周长取最小值时，PQ所在直线的解析式是（）

A . y=x B . y=x+1 C . y=x+2 D . y=x+3

查看解析收藏纠错

+选题
38. 如图，一次函数y=-x+b的图象与反比例函数y= $\text{[math]}$ (x>0)的图象交于A(1，m)，B(3，n)两点．

（1）求一次函数及反比例函数的表达式；

（2）
点P为双曲线上A，B之间的一点，求当△ABP的面积最大时点P的坐标
.

查看解析收藏纠错

+选题
39. 如图，在平面直角坐标系 $\text{[math]}$ 中，等腰直角三角形 $\text{[math]}$ 的直角顶点 $\text{[math]}$ ，顶点A、 $\text{[math]}$ 恰好落在反比例函数 $\text{[math]}$ 第一象限的图象上．

（1）分别求反比例函数的表达式和直线 $\text{[math]}$ 所对应的一次函数的表达式；

（2）在x轴上是否存在一点P，使 $\text{[math]}$ 周长的值最小．若存在，求出最小值；若不存在，请说明理由．

查看解析收藏纠错

+选题
40. 我们已经学习了正比例函数 $\text{[math]}$ 和反比例函数 $\text{[math]}$ 的图象和性质，下面，我们研究函数 $\text{[math]}$ 的图象和性质，我们不妨特殊化，设 $\text{[math]}$ ， $\text{[math]}$ ，即 $\text{[math]}$ .

（1） ① 函数 $\text{[math]}$ 的自变量x的取值范围是 ▲ ；
②容易发现，当 $\text{[math]}$ 时， $\text{[math]}$ ；当 $\text{[math]}$ 时， $\text{[math]}$ .由此可见，图象在第 ▲ 象限；

③阅读材料：当 $\text{[math]}$ 时， $\text{[math]}$ .当 $\text{[math]}$ 时，即 $\text{[math]}$ ， $\text{[math]}$ 有最小值是2.请仿照上述过程，求出当 $\text{[math]}$ 时， $\text{[math]}$ 的最大值；

（2）为了画函数 $\text{[math]}$ 的图象，小明通过列表，描点画出了下图，请连线；

（3）观察图象，当 $\text{[math]}$ 随着 $\text{[math]}$ 的增大而增大时，自变量x的取值范围是；

（4）某隧道长185m，一个匀速前进的车队有10辆车，每辆车长4m，相邻两车的距离d（m）与车速v（m/s）的关系式为 $\text{[math]}$ ，求自第1辆车车头进隧道至第10辆车车尾出隧道所用时间的最小值.

查看解析收藏纠错

+选题
41. 阅读理解：已知：对于实数a≥0，b≥0，满足a+b≥2 $\text{[math]}$ ，当且仅当a = b时，等号成立，此时取得代数式a+b的最小值.
根据以上结论，解决以下问题：

（1）拓展：若a>0，当且仅当a=时，a+ $\text{[math]}$ 有最小值，最小值为；

（2）应用：
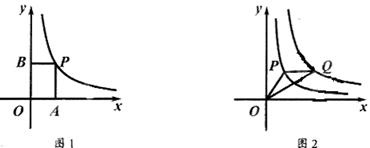
①如图1，已知点P为双曲线y= $\text{[math]}$ (x>0)上的任意一点，过点P作PA⊥x轴，PB丄y轴，四边形OAPB的周长取得最小值时，求出点P的坐标以及周长最小值：

②如图2，已知点Q是双曲线y= $\text{[math]}$ (x>0)上一点，且PQ∥x轴，连接OP、OQ，当线段OP取得最小值时，在平面内取一点C，使得以0、P、Q、C为顶点的四边形是平行四边形，求出点C的坐标.

查看解析收藏纠错

+选题
42. 如图，直线 $\text{[math]}$ 与双曲线 $\text{[math]}$ 相交于A、B两点，以AB为边作正方形ABCD，则正方形ABCD面积的最小值为．

查看解析收藏纠错

+选题

2024年浙教版数学八（下）微素养核心突破25 反比例函数与几何综合

一、公共点问题

二、三角形问题

三、四边形问题

四、构造全等三角形

五、最值问题

相关试卷收起∨

2024年浙教版数学八（下）微素养核心突破25 反比例函数与几何综合

一、公共点问题

二、三角形问题

三、四边形问题

四、构造全等三角形

五、最值问题

相关试卷 收起∨

相关试卷收起∨