修改时间:2021-08-25 浏览次数:220 类型:二轮复习
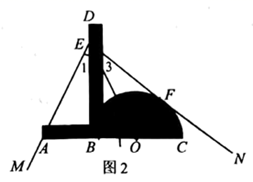
使用方法如图2所示,若要把 三等分,只需适当放置三分角器,使
经过
的顶点
,点
落在边
上,半圆O与另一边
恰好相切,切点为F,则
就把
三等分了.
为了说明这一方法的正确性,需要对其进行证明.如下给出了不完整的“已知”和“求证”,请补充完整,并写出“证明”过程.

已知:如图2,点在 同一直线上,
垂足为点B, ▲
求证: ▲
如图,点D是弧 上一动点,线段
点A是线段
的中点,过点C作
,交
的延长线于点F.当
为等腰三角形时,求线段
的长度.

小亮分析发现,此问题很难通过常规的推理计算彻底解决,于是尝试结合学习函数的经验研究此问题,请将下面的探究过程补充完整:
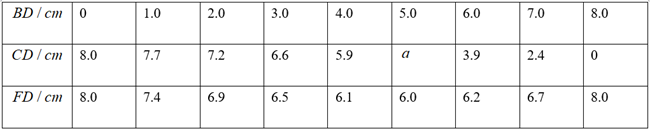
操作中发现:
①"当点D为弧 的中点时,
".则上中a的值是
②"线段 的长度无需测量即可得到".请简要说明理由;
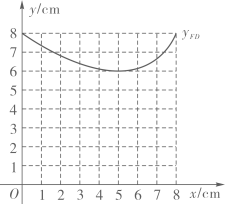

已知:如图1, 及
上一点P.
求作:直线PQ,使得PQ与 相切.
作法:如图2,
①连接PO并延长交 于点A;
②在 上任取一点B(点P,A除外),以点B为圆心,BP长为半径作
,与射线PO的另一个交点为C.
③连接CB并延长交 于点Q.
④作直线PQ;
所以直线PQ就是所求作的直线.
根据小石设计的尺规作图的过程.
证明:∵CQ是的 直径,
∴ __▲__
(__▲__)(填推理的依据)
∴ .
又∵OP是 的半径,
∴PQ是 的切线(_▲_)(填推理的依据)
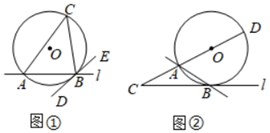
已知:如图①,直线l与⊙O相交于点A、B,过点B作.
求证:∠ABD=.
|
小明:如图1,(1)分别在射线 由作图, 小军:我认为小明的作图方法很有创意,但是大麻烦了,可以改进如下,如图2.(1)分别在射线 …… |
任务:
① ;②
;③
;④
;⑤
.
试题篮