苏科版备考2021年中考数学三轮冲刺专题10 数学思维及能力建设

修改时间：2021-05-26 浏览次数：227 类型：三轮冲刺编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、单选题

1. 欧几里得的《原本》记载，形如x²＋ax＝b²的方程的图，解法是：画Rt△ABC，使∠ACB＝90°，BC＝ $\text{[math]}$ ，AC＝b，再在斜边AB上截取BD＝ $\text{[math]}$ .则该方程的一个正根是（）

A . AC的长 B . AD的长 C . BC的长 D . CD的长

查看解析收藏纠错

+选题
2. 以 $\text{[math]}$ 为边画出四边形 $\text{[math]}$ ，可以画出的四边形个数为（）

A . 0 B . 1 C . 2 D . 无限多

查看解析收藏纠错

+选题
3. 已知二次函数 $\text{[math]}$ （m为常数），当 $\text{[math]}$ 时， $\text{[math]}$ 的最大值是15，则 $\text{[math]}$ 的值是（）

A . -10和6 B . -19和 $\text{[math]}$ C . 6和 $\text{[math]}$ D . -19和6

查看解析收藏纠错

+选题
4. 按照如图所示的流程，若输出的 $\text{[math]}$ ，则输入的m为（）

A . 3 B . 1 C . 0 D . -1

查看解析收藏纠错

+选题
5. 《庄子》一书里有：“一尺之棰（木棍），日取其半，万世不竭（尽，完）”这句话可以用数学符号表示：1＝ $\text{[math]}$ +…+ $\text{[math]}$ +…；也可以用图形表示．上述研究问题的过程中体现的主要数学思想是（　　）

A . 函数思想 B . 数形结合思想 C . 公理化思想 D . 分类讨论思想

查看解析收藏纠错

+选题
6. 我们解一元二次方程3x²-6x=0时，可以运用因式分解法，将此方程化为3x（x-2）=0，从而得到两个一元一次方程：3x=0或x-2=0，进而得到原方程的解为 $\text{[math]}$ =0，x₂=2．这种解法体现的数学思想是（）

A . 转化思想 B . 函数思想 C . 数形结合思想 D . 公理化思想

查看解析收藏纠错

+选题
7. 如图，平面直角坐标系中， $\text{[math]}$ 与 $\text{[math]}$ 轴分别交于 $\text{[math]}$ 、 $\text{[math]}$ 两点，点 $\text{[math]}$ 的坐标为 $\text{[math]}$ ， $\text{[math]}$ ．将 $\text{[math]}$ 沿着与 $\text{[math]}$ 轴平行的方向平移多少距离时 $\text{[math]}$ 与 $\text{[math]}$ 轴相切（）

A . 1 B . 2 C . 3 D . 1或3

查看解析收藏纠错

+选题
8. 以坐标原点O为圆心，作半径为1的圆，若直线 $\text{[math]}$ 与⊙O相交，则b的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
9. 探究课上，老师给出一个问题“利用二次函数y＝2x²与一次函数y＝x+2的图象，求一元二次方程2x²＝x+2的近似根”小华利用计算机绘制出如图所示的图象，通过观察可知该方程的两近似根x₁和x₂满足﹣1＜x₁＜0，1＜x₂＜2．小华的上述方法体现的数学思想是（　　）

A . 公理化 B . 分类讨论 C . 数形结合 D . 由特殊到一般

查看解析收藏纠错

+选题
10. “已知二次函数y＝ax²+bx+c的图象如图所示，试判断a+b+c与0的大小.”一同学是这样回答的：“由图象可知：当x＝1时y＜0，所以a+b+c＜0.”他这种说明问题的方式体现的数学思想方法叫做（）

A . 换元法 B . 配方法 C . 数形结合法 D . 分类讨论法

查看解析收藏纠错

+选题
11.
我国古代《易经》一书中记载，远古时期，人们通过在绳子上打结来记录数量，即“结绳计数”．如图，一位母亲在从右到左依次排列的绳子上打结，满七进一，用来记录孩子自出生后的天数，由图可知，孩子自出生后的天数是（）

A . 84 B . 336 C . 510 D . 1326

查看解析收藏纠错

+选题
12. 在平面直角坐标系中，横坐标和纵坐标都是整数的点叫做整点，已知直线 $\text{[math]}$ （ $\text{[math]}$ ）与两坐标轴围成的三角形区域（不含边界）中有且只有四个整点，则t的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$ 且 $\text{[math]}$

查看解析收藏纠错

+选题

二、填空题

13. 当 $\text{[math]}$ 时，反比例函数 $\text{[math]}$ （ $\text{[math]}$ 且 $\text{[math]}$ ）的最大值与最小值之差是1，则 $\text{[math]}$ 的值是.

查看解析收藏纠错

+选题
14. 已知一个三角形的三边都是方程 $\text{[math]}$ 的根，则此三角形的周长为．

查看解析收藏纠错

+选题
15. 在矩形ABCD中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 是边 $\text{[math]}$ 的三等分点， $\text{[math]}$ 与 $\text{[math]}$ 交于点 $\text{[math]}$ ，则 $\text{[math]}$ .

查看解析收藏纠错

+选题
16. 如图，在等边△ABC中，AB＝4cm，点M为边BC的中点，点N为边AB上的任意一点（不与点A，B重合）．若点B关于直线MN的对称点B'恰好落在等边△ABC的边上，则BN的长为cm．

查看解析收藏纠错

+选题
17. 已知二次函数y=x²﹣2mx（m为常数），当﹣1≤x≤2时，函数值y的最小值为﹣2，则m的值是．

查看解析收藏纠错

+选题
18. 甲乙两运动员乒乓球比赛正在进行中，甲必须再胜2局才能最后获胜；乙必须再胜3局才能最后获胜. 若甲、乙两人每局取胜的概率都是 $\text{[math]}$ ，则甲最后获胜的概率是.

查看解析收藏纠错

+选题
19. 将奇数1、3、5、…、2007、2009从小到大排成一个多位数A=13579111315…20072009，从A中截出能被5整除的五位数，则所有的这种五位数中，最小数是，最大数是。

查看解析收藏纠错

+选题
20. 如图，O是等边△ABC外接圆的圆心，连结OA、OB、OC ，以点A为圆心，以⊙O的直径为半径画弧分别交AB、AC的延长线于点D、E ．若OA=2，则图中阴影部分图形的面积和为(结果保留根号和π)．

查看解析收藏纠错

+选题
21. P为⊙O内一点，OP＝3cm ， ⊙O的半径为5cm ，则经过P点的最短弦长为cm ，最长弦长为cm ．

查看解析收藏纠错

+选题
22. 数轴上 $\text{[math]}$ 两点的距离为4，一动点 $\text{[math]}$ 从点 $\text{[math]}$ 出发，按以下规律跳动：第1次跳动到 $\text{[math]}$ 的中点 $\text{[math]}$ 处，第2次从 $\text{[math]}$ 点跳动到 $\text{[math]}$ 的中点 $\text{[math]}$ 处，第3次从 $\text{[math]}$ 点跳动到 $\text{[math]}$ 的中点 $\text{[math]}$ 处．按照这样的规律继续跳动到点 $\text{[math]}$ （ $\text{[math]}$ ， $\text{[math]}$ 是整数）处，那么线段 $\text{[math]}$ 的长度为（ $\text{[math]}$ ， $\text{[math]}$ 是整数）．

查看解析收藏纠错

+选题
23. 已知△ABC是等腰直角三角形，AB＝AC ， D为平面内的任意一点，且满足CD＝AC ，若△ADB是以AD为腰的等腰三角形，则∠CDB的度数为．

查看解析收藏纠错

+选题
24. 幻方是相当古老的数学问题，我国古代的《洛书》中记载了最早的幻方---九宫图.将数字1~9分别填入如图所示的幻方中，要求每一横行、每一竖行以及两条斜对角线上的数字之和都是15，则m的值为.

查看解析收藏纠错

+选题
25. 已知关于x的一元二次方程x²+ax+nb＝0（1≤n≤3，n为整数），其中a是从2、4、6三个数中任取的一个数，b是从1、3、5三个数中任取的一个数，定义“方程有实数根”为事件A_n（n＝1，2，3），当A_n的概率最小时，n的所有可能值为．

查看解析收藏纠错

+选题
26. 我国南宋著名数学家秦九韶在他的著作《数书九章》一书中，给出了著名的秦九韶公式，也叫三斜求积公式，即如果一个三角形的三边长分别为a，b，c，则该三角形的面积为s＝ $\text{[math]}$ .已知△ABC的三边长分别为 $\text{[math]}$ ，2，2，则△ABC的面积为.

查看解析收藏纠错

+选题
27. 四边形两对角线的交点为，用四种颜色给 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 染色，使得有公共边的三角形不同色，那么有种染色方法.

查看解析收藏纠错

+选题
28. 已知y = | x － 1 | x + | x －2 | ( x － 1 )，则不等式 y < 0的解集为 .

查看解析收藏纠错

+选题
29. 如图，圆心都在x轴正半轴上的半圆O₁ ，半圆O₂ ， …，半圆O_n与直线l相切．设半圆O₁ ，半圆O₂ ， …，半圆O_n的半径分别是r₁ ， r₂ ， …，r_n ，则当直线l与x轴所成锐角为30°，且r₁＝1时，r₂₀₁₈＝.

查看解析收藏纠错

+选题

30. 小亮在匀速行驶的汽车里，注意到公路里程碑上的数如下表所示：

时刻	12：00	13：00	16：00
里程碑上的数	是一个两位数	十位数字和个位数字与12：00时所看到的正好颠倒了	比12：00时看到的两位数中间多了个0

12：00时看到的两位数是

查看解析收藏纠错

+选题

31. 著名的斐波那契数列1、2、3、5、8、13、21、…，其中的第9个数是．

查看解析收藏纠错

+选题
32. 如图，将一个8cm×16cm智屏手机抽象成一个矩形ABCD ，其中AB＝8cm ， AD＝16cm ，现将正在竖屏看视频的这个手机围绕它的中心R顺时针旋转90°后改为横屏看视频，其中，M是CD的中点，则图中等于45°的角有个．（按图中所标字母写出符合条件的角）

查看解析收藏纠错

+选题

三、解答题

33. “通过等价变换，化陌生为熟悉，化未知为已知”是数学学习中解决问题的基本思维方式，例如：解方程 $\text{[math]}$ ，就可以利用该思维方式，设 $\text{[math]}$ ，将原方程转化为： $\text{[math]}$ 这个熟悉的关于y的一元二次方程，解出y，再求x，这种方法又叫“换元法”．请你用这种思维方式和换元法解决下面的问题．已知实数x，y满足 $\text{[math]}$ ，求 $\text{[math]}$ 的值．

查看解析收藏纠错

+选题
34. m是什么整数时，方程（m²﹣1）x²﹣6（3m﹣1）x+72＝0有两个不相等的正整数根．

查看解析收藏纠错

+选题
35. 如图

（1）如图，矩形ABCD的对角线长为a ，对角线与一边的夹角为α（α≤45°），则CD＝（用α的三角函数和a来表示），S_△_BCD＝（用α的三角函数和a来表示）＝（用2α的三角函数和a来表示）；

（2）猜想并直接写出sin2α，sinα，cosα之间的数量关系．

查看解析收藏纠错

+选题
36. 我们学习过利用用尺规作图平分一个任意角，而“利用尺规作图三等分一个任意角”曾是数学史上一大难题，之后被数学家证明是不可能完成的人们根据实际需爱，发明了一种简易操作工具--------三分角器.图1是它的示意图，其中 $\text{[math]}$ 与半圆O的直径 $\text{[math]}$ 在同一直线上，且 $\text{[math]}$ 的长度与半圆的半径相等； $\text{[math]}$ 与 $\text{[math]}$ 重直F点 $\text{[math]}$ 足够长.
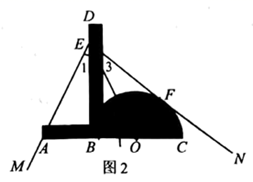
使用方法如图2所示，若要把 $\text{[math]}$ 三等分，只需适当放置三分角器，使 $\text{[math]}$ 经过 $\text{[math]}$ 的顶点 $\text{[math]}$ ，点 $\text{[math]}$ 落在边 $\text{[math]}$ 上，半圆O与另一边 $\text{[math]}$ 恰好相切，切点为F，则 $\text{[math]}$ 就把 $\text{[math]}$ 三等分了.

为了说明这一方法的正确性，需要对其进行证明.如下给出了不完整的“已知”和“求证”，请补充完整，并写出“证明”过程.

已知：如图2，点在 $\text{[math]}$ 同一直线上， $\text{[math]}$ 垂足为点B， ▲

求证： ▲

查看解析收藏纠错

+选题
37. 在“看图说故事”活动中，某学习小组结合图象设计了一个问题情境．

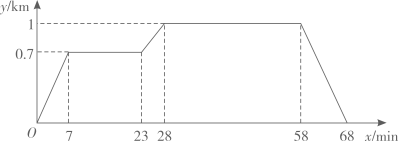
已知小亮所在学校的宿舍、食堂、图书馆依次在同一条直线上，食堂离宿舍 $\text{[math]}$ ，图书馆离宿舍 $\text{[math]}$ ．周末，小亮从宿舍出发，匀速走了 $\text{[math]}$ 到食堂；在食堂停留 $\text{[math]}$ 吃早餐后，匀速走了 $\text{[math]}$ 到图书馆；在图书馆停留 $\text{[math]}$ 借书后，匀速走了 $\text{[math]}$ 返回宿舍，给出的图象反映了这个过程中小亮离宿舍的距离 $\text{[math]}$ 与离开宿舍的时间 $\text{[math]}$ 之间的对应关系．

请根据相关信息，解答下列问题：

（1）填表：

离开宿舍的时间/ $\text{[math]}$

2

5

20

23

30

离宿舍的距离/ $\text{[math]}$

0.2

0.7

（2）填空：
①食堂到图书馆的距离为 $\text{[math]}$ ．

②小亮从食堂到图书馆的速度为 $\text{[math]}$ ．

③小亮从图书馆返回宿舍的速度为 $\text{[math]}$ ．

④当小亮离宿舍的距离为 $\text{[math]}$ 时，他离开宿舍的时间为 $\text{[math]}$ ．

（3）当 $\text{[math]}$ 时，请直接写出y关于x的函数解析式．

查看解析收藏纠错

+选题
38. 如图，在△ABC中，AB＝8cm，BC＝16cm，点P从点A开始沿边AB向点B以2cm/s的速度移动，点Q从点B开始沿边BC向点C以4cm/s的速度移动，如果点P、Q分别从点A、B同时出发，经几秒钟△PBQ与△ABC相似？试说明理由．

查看解析收藏纠错

+选题
39. 如图，△ABC的边BC在直线l上，AD是△ABC的高，∠ABC=45°，BC=6cm，AB=2 $\text{[math]}$ cm．点P从点B出发沿BC方向以1cm/s速度向点C运动，当点P到点C时，停止运动．PQ⊥BC，PQ交AB或AC于点Q，以PQ为一边向右侧作矩形PQRS，PS=2PQ．矩形PQRS与△ABC的重叠部分的面积为S（cm²），点P的运动时间为t（s）．回答下列问题：

（1） AD=cm；

（2）当点R在边AC上时，求t的值；

（3）求S与t之间的函数关系式．

查看解析收藏纠错

+选题

离开宿舍的时间/ $\text{[math]}$	2	5	20	23	30
离宿舍的距离/ $\text{[math]}$	0.2		0.7

苏科版备考2021年中考数学三轮冲刺专题10 数学思维及能力建设

一、单选题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨