河南省中考数学真题模拟题分类卷5 图形的变换及锐角三角函数（近几年）

修改时间：2021-08-25 浏览次数：192 类型：二轮复习编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、单选题

1. 如下摆放的几何体中，主视图与左视图有可能不同的是（）

A . B . C . D .

查看解析收藏纠错

+选题
2. 如图①是由大小相同的小正方体搭成的几何体，将上层的小正方体平移后得到图②.关于平移前后几何体的三视图，下列说法正确的是（）

A . 主视图相同 B . 左视图相同 C . 俯视图相同 D . 三种视图都不相同

查看解析收藏纠错

+选题
3. 如图，胶带的左视图是（）

A . B . C . D .

查看解析收藏纠错

+选题
4. 如图是由7个相同的小正方体搭成的几何体，在标号为①的小正方体上方添加一个小正方体后，所得几何体的三视图与原几何体的三视图相比没有发生变化的是（）

A . 主视图和俯视图 B . 主视图和左视图 C . 左视图和俯视图 D . 主视图、左视图和俯视图

查看解析收藏纠错

+选题
5. 下列立体图形的主视图与左视图相同是（）

A . ①②③ B . ②③ C . ①②④ D . ①②③④

查看解析收藏纠错

+选题
6. 小敏计划在暑假参加海外游学，她打算制作一个正方体礼盒送给外国朋友.如图所示是她设计的礼盒的平面展开图，请你判断，正方体礼盒上与“孝”字相对的面上的字是（）

A . 义 B . 仁 C . 智 D . 信

查看解析收藏纠错

+选题
7. 如图，由5个完全相同的小正方体组合成一个立体图形，它的俯视图是（）

A . B . C . D .

查看解析收藏纠错

+选题
8. 如图是由8个相同的小正方体组成的几何体，其主视图是（）

A . B . C . D .

查看解析收藏纠错

+选题
9. 如图， $\text{[math]}$ 的顶点 $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 在 $\text{[math]}$ 轴的正半轴上，延长 $\text{[math]}$ 交 $\text{[math]}$ 轴于点 $\text{[math]}$ .将 $\text{[math]}$ 绕点 $\text{[math]}$ 顺时针旋转得到 $\text{[math]}$ ，当点 $\text{[math]}$ 的对应点 $\text{[math]}$ 落在 $\text{[math]}$ 上时， $\text{[math]}$ 的延长线恰好经过点 $\text{[math]}$ ，则点 $\text{[math]}$ 的坐标为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
10. 某正方体的每个面上都有一个汉字，如图是它的一种展开图，那么在原正方体中，与“国”字所在面相对的面上的汉字是（）

A . 厉 B . 害 C . 了 D . 我

查看解析收藏纠错

+选题
11. 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，以点 $\text{[math]}$ 为圆心， $\text{[math]}$ 的长为半径作弧交 $\text{[math]}$ 于点 $\text{[math]}$ ，再分别以点 $\text{[math]}$ ， $\text{[math]}$ 为圆心，大于 $\text{[math]}$ 的长为半径作弧，两弧交于点 $\text{[math]}$ ，作射线 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ．若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题

二、填空题

12. 小华用一张直角三角形纸片玩折纸游戏，如图1，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .第一步，在 $\text{[math]}$ 边上找一点 $\text{[math]}$ ，将纸片沿 $\text{[math]}$ 折叠，点 $\text{[math]}$ 落在 $\text{[math]}$ 处，如图2，第二步，将纸片沿 $\text{[math]}$ 折叠，点 $\text{[math]}$ 落在 $\text{[math]}$ 处，如图3.当点 $\text{[math]}$ 恰好在原直角三角形纸片的边上时，线段 $\text{[math]}$ 的长为.

查看解析收藏纠错

+选题
13. 如图，∠MAN=90°，点C在边AM上，AC=4，点B为边AN上一动点，连接BC，△A′BC与△ABC关于BC所在直线对称，点D，E分别为AC，BC的中点，连接DE并延长交A′B所在直线于点F，连接A′E．当△A′EF为直角三角形时，AB的长为．

查看解析收藏纠错

+选题
14. 如图，在矩形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，对角线 $\text{[math]}$ ， $\text{[math]}$ 交于点 $\text{[math]}$ ，点 $\text{[math]}$ 是 $\text{[math]}$ 边上一动点．将 $\text{[math]}$ 沿 $\text{[math]}$ 翻折得到 $\text{[math]}$ ， $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，且点 $\text{[math]}$ 在 $\text{[math]}$ 下方，连接 $\text{[math]}$ ．当 $\text{[math]}$ 是直角三角形时， $\text{[math]}$ 的周长为．

查看解析收藏纠错

+选题
15. 如图，在周长为16，面积为6的矩形纸片 $\text{[math]}$ 中， $\text{[math]}$ 是 $\text{[math]}$ 的中点. $\text{[math]}$ 是 $\text{[math]}$ 上一动点，将 $\text{[math]}$ 沿直线 $\text{[math]}$ 折叠，点 $\text{[math]}$ 落在点 $\text{[math]}$ 处.在 $\text{[math]}$ 上任取一点 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的最小值为.

查看解析收藏纠错

+选题
16. 如图，Rt△ABC中，∠ACB＝90°，∠A＝30°，BC＝6，D，E分别是AB，AC边的中点，将△ABC绕点B顺时针旋转60°到△A′BC′的位置，则整个旋转过程中线段DE所扫过部分的面积（即图中阴影部分面积）为.

查看解析收藏纠错

+选题
17. 已知：Rt△ABC中，∠B=90°，AB=4，BC=3，点M、N分别在边AB、AC上，将△AMN沿直线MN折叠，点A落在点P处，且点P在射线CB上，当△PNC为直角三角形时，PN的长为.

查看解析收藏纠错

+选题
18. 如图，在正方形 $\text{[math]}$ 外作等腰直角三角形 $\text{[math]}$ ，连接 $\text{[math]}$ ，则 $\text{[math]}$ .

查看解析收藏纠错

+选题
19. 如图，在矩形ABCD中， $\text{[math]}$ ， $\text{[math]}$ ，点E在边BC上，且 $\text{[math]}$ .连接AE，将 $\text{[math]}$ 沿AE折叠，若点B的对应点 $\text{[math]}$ 落在矩形ABCD的边上，则a的值为.

查看解析收藏纠错

+选题
20. 如图，在矩形ABCD中，AB＝6，BC＝12，点E在边BC上，且BE＝2CE，将矩形沿过点E的直线折叠，点C，D的对应点分别为C′，D′，折痕与边AD交于点F，当点B，C′，D′恰好在同一直线上时，AF的长为.

查看解析收藏纠错

+选题

三、解答题

21. 开凿于北魏孝文帝年间的龙门石窟是中国石刻艺术瑰宝，卢舍那佛像是石窟中最大的佛像.某数学活动小组到龙门石窟景区测量这尊佛像的高度.如图，他们选取的测量点 $\text{[math]}$ 与佛像 $\text{[math]}$ 的底部 $\text{[math]}$ 在同一水平线上.已知佛像头部 $\text{[math]}$ 为 $\text{[math]}$ ，在 $\text{[math]}$ 处测得佛像头顶部 $\text{[math]}$ 的仰角为 $\text{[math]}$ ，头底部 $\text{[math]}$ 的仰角为 $\text{[math]}$ ，求佛像 $\text{[math]}$ 的高度（结果精确到 $\text{[math]}$ .参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）

查看解析收藏纠错

+选题
22. 数学兴趣小组到黄河风景名胜区测量炎帝塑像（塑像中高者）的高度.如图所示，炎帝塑像DE在高55m的小山EC上，在A处测得塑像底部E的仰角为34°，再沿AC方向前进21m到达B处，测得塑像顶部D的仰角为60°，求炎帝塑像DE的高度.（精确到1m.参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）

查看解析收藏纠错

+选题
23. “高低杠”是女子体操特有的一个竞技项目，其比赛器材由高、低两根平行杠及若干支架组成，运动员可根据自己的身高和习惯在规定范围内调节高、低两杠间的距离．某兴趣小组根据高低杠器材的一种截面图编制了如下数学问题，请你解答．
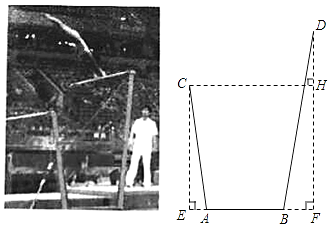
如图所示，底座上A，B两点间的距离为90cm．低杠上点C到直线AB的距离CE的长为155cm，高杠上点D到直线AB的距离DF的长为234cm，已知低杠的支架AC与直线AB的夹角∠CAE为82.4°，高杠的支架BD与直线AB的夹角∠DBF为80.3°．求高、低杠间的水平距离CH的长．（结果精确到1cm，参考数据sin82.4°≈0.991，cos82.4°≈0.132，tan82.4°≈7.500，sin80.3°≈0.983，cos80.3°≈0.168，tan80.3°≈5.850）

查看解析收藏纠错

+选题
24. 如图，某公园有一小亭 $\text{[math]}$ ，它周围350米内是文物保护区.某勘探队员在公园由西向东行走，在 $\text{[math]}$ 处测得小亭 $\text{[math]}$ 在北偏东 $\text{[math]}$ 的方向上，若勘探队员行走的速度是每分钟60米，从点 $\text{[math]}$ 走到点 $\text{[math]}$ 需要20分钟，此时测得小亭 $\text{[math]}$ 在北偏西 $\text{[math]}$ 的方向上.若该公园打算沿射线 $\text{[math]}$ 的方向修一条笔直的小路，则此小路是否会通过文物保护区？请说明理由.（结果保留整数.参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）

查看解析收藏纠错

+选题
25. 如图，一艘游轮在海面上点O处遇到大雾，向位于A处的救援船发出求救信号，救援船指定B地为相遇地点，其中游轮在救援船的北偏西51°方向上，在相遇点B的南偏西54°方向上，相遇点B在救援船的北偏东9°方向上，救援船以50海里/时的速度行驶2小时到达B地.若游轮的速度是30海里/时，求游轮用多长时间能到达B地.(结果保留一位小数.参考数据： $\text{[math]}$ ≈1.41， $\text{[math]}$ ≈1.73)

查看解析收藏纠错

+选题
26. 疫情期间，为了保障大家的健康，各地采取了多种方式进行预防，某地利用无人机规劝居民回家.如图，一条笔直的街道 $\text{[math]}$ ，在街道 $\text{[math]}$ 处的正上方 $\text{[math]}$ 处有一架无人机，该无人机在 $\text{[math]}$ 处测得俯角为 $\text{[math]}$ 的街道 $\text{[math]}$ 处有人聚集，然后沿平行于街道 $\text{[math]}$ 的方向再向前飞行60米到达 $\text{[math]}$ 处，在 $\text{[math]}$ 处测得俯角为 $\text{[math]}$ 的街道 $\text{[math]}$ 处也有人聚集，已知两处聚集点 $\text{[math]}$ 之间的距离为120米，求无人机飞行的高度 $\text{[math]}$ .(参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ )

查看解析收藏纠错

+选题

四、综合题

27. 位于河南省登封市境内的元代观星台，是中国现存最早的天文台，也是世界文化遗产之一.

某校数学社团的同学们使用卷尺和自制的测角仪测量观星台的高度.如图所示，他们在地面一条水平步道 $\text{[math]}$ 上架设测角仪，先在点M处测得观星台最高点A的仰角为 $\text{[math]}$ ，然后沿 $\text{[math]}$ 方向前进 $\text{[math]}$ 到达点N处，测得点 $\text{[math]}$ 的仰角为 $\text{[math]}$ .测角仪的高度为 $\text{[math]}$ ，

（1）求观星台最高点A距离地面的高度(结果精确到 $\text{[math]}$ .参考数据： $\text{[math]}$ )；

（2） “景点简介”显示，观星台的高度为 $\text{[math]}$ ，请计算本次测量结果的误差，并提出一条减小误差的合理化建议.

查看解析收藏纠错

+选题
28. 如图

（1）问题发现
如图1，在△OAB和△OCD中，OA=OB，OC=OD，∠AOB=∠COD=40°，连接AC，BD交于点M．填空：
① $\text{[math]}$ 的值为；
②∠AMB的度数为．

（2）类比探究
如图2，在△OAB和△OCD中，∠AOB=∠COD=90°，∠OAB=∠OCD=30°，连接AC交BD的延长线于点M．请判断 $\text{[math]}$ 的值及∠AMB的度数，并说明理由；

（3）拓展延伸
在（2）的条件下，将△OCD绕点O在平面内旋转，AC，BD所在直线交于点M，若OD=1，OB= $\text{[math]}$ ，请直接写出当点C与点M重合时AC的长．

查看解析收藏纠错

+选题
29. 中原福塔，又名“河南广播电视塔”，是郑州市著名地标之一．小明和小亮利用卷尺和自制的测角仪测量福塔的高度．如图，小明站在点 $\text{[math]}$ 处测得福塔顶端 $\text{[math]}$ 的仰角为 $\text{[math]}$ ，小亮站在点 $\text{[math]}$ 处测得福塔顶端 $\text{[math]}$ 的仰角为 $\text{[math]}$ ．已知测角仪高度为 $\text{[math]}$ ，两人相距 $\text{[math]}$ （点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 在一条直线上）．

（1）求中原福塔 $\text{[math]}$ 的高度；(结果精确到 $\text{[math]}$ ．参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ )

（2） “景点简介”显示，中原福塔总高 $\text{[math]}$ ．请计算本次测量结果的误差，并提出一条减小误差的合理化建议．

查看解析收藏纠错

+选题
30. 如图，某人在山坡坡脚 $\text{[math]}$ 处测得一座建筑物顶点 $\text{[math]}$ 的仰角为 $\text{[math]}$ ，沿山坡向上走到 $\text{[math]}$ 处再测得该建筑物顶点 $\text{[math]}$ 的仰角为 $\text{[math]}$ .已知 $\text{[math]}$ 米， $\text{[math]}$ ， $\text{[math]}$ 的延长线交于点 $\text{[math]}$ ，山坡坡度为 $\text{[math]}$ （即 $\text{[math]}$ ）.注：取 $\text{[math]}$ 为 $\text{[math]}$ .

（1）求该建筑物的高度（即 $\text{[math]}$ 的长）.

（2）求此人所在位置点 $\text{[math]}$ 的铅直高度（测倾器的高度忽略不计）.

（3）若某一时刻， $\text{[math]}$ 米长木棒竖放时，在太阳光线下的水平影长是 $\text{[math]}$ 米，则同一时刻该座建筑物顶点 $\text{[math]}$ 投影与山坡上点 $\text{[math]}$ 重合，求点 $\text{[math]}$ 到该座建筑物的水平距离.

查看解析收藏纠错

+选题

31. 蔡明园公园位于河南省驻马店市上蔡县蔡都镇西南部，其公园南山门被誉为“亚洲第一门”，学完了三角函数知识后，某数学“综合与实践”小组的同学把“测量南山门最高点的高度”作为一项课题活动，他们制定了测量方案，并利用课余时间完成了实地测量.为了减小测量误差，小组在测量仰角以及两点间的距离时，都分别测量了两次并取它们的平均值作为测量结果，测量数据如表：

课题	测量南山门最高点的高度
实物图
成员	组长：xxx 组员：xxx，xxx，xxx
测量工具	卷尺、测角仪……
测量示意图				说明：AB表示南山门最高点到地面的竖直距离.测角仪的高度CD-EF-1.5m点C.F与点B在同一直线上，点C.F之间的距离可直接测将，且点A、B.C.D.E、F在同一平面内.
测量数据	第一次	第二次	平均值
	35.95°	36.05°	36°
	45.09°	44.91°	45°
	79.58m	79.62m	79.6m
……	……

（1）请帮助该小组的同学根据上表中的测量数据，求南山门最高点的高度AB.（结果精确到0.1m，参考数据：sin36°≈0.59，cos36°≈0.81，tan36°≈0.73， $\text{[math]}$ ≈1.41）

（2）该小组要写出一份完整的课题活动报告，除上表中的项目外，你认为还需要补充哪些项目？（写出一个即可）（如需作图或作辅助线，请先将原题草图画在对应题目的答题区域后再作答.）

查看解析收藏纠错

+选题

32. 在古代，智慧的劳动人民已经会使用“石磨”，其原理为在磨盘的边缘连接一个固定长度的“连杆”，推动“连杆”带动磨盘转动，将粮食磨碎，物理学上称这种动力传输工具为“曲柄连杆机构”.小明受此启发设计了一个“双连杆机构”，设计图如图1，两个固定长度的“连杆” $\text{[math]}$ ， $\text{[math]}$ 的连接点 $\text{[math]}$ 在 $\text{[math]}$ 上，当点 $\text{[math]}$ 在 $\text{[math]}$ 上转动时，带动点 $\text{[math]}$ ， $\text{[math]}$ 分别在射线 $\text{[math]}$ ， $\text{[math]}$ 上滑动， $\text{[math]}$ .当 $\text{[math]}$ 与 $\text{[math]}$ 相切时，点 $\text{[math]}$ 恰好落在 $\text{[math]}$ 上，如图2.

请仅就图2的情形解答下列问题.

（1）求证： $\text{[math]}$ ；

（2）若 $\text{[math]}$ 的半径为 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长.

查看解析收藏纠错

+选题
33. 将正方形 $\text{[math]}$ 的边 $\text{[math]}$ 绕点A逆时针旋转至 $\text{[math]}$ ，记旋转角为 $\text{[math]}$ .连接 $\text{[math]}$ ，过点D作 $\text{[math]}$ 垂直于直线 $\text{[math]}$ ，垂足为点E，连接 $\text{[math]}$ ，

（1）如图1，当 $\text{[math]}$ 时， $\text{[math]}$ 的形状为，连接 $\text{[math]}$ ，可求出 $\text{[math]}$ 的值为；

（2）当 $\text{[math]}$ 且 $\text{[math]}$ 时，
①（1）中的两个结论是否仍然成立?如果成立，请仅就图2的情形进行证明；如果不成立，请说明理由；

②当以点 $\text{[math]}$ 为顶点的四边形是平行四边形时，请直接写出 $\text{[math]}$ 的值.

查看解析收藏纠错

+选题
34. 在 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .点P是平面内不与点A，C重合的任意一点.连接AP，将线段AP绕点P逆时针旋转α得到线段DP，连接AD，BD，CP.

（1）观察猜想
如图1，当 $\text{[math]}$ 时， $\text{[math]}$ 的值是，直线BD与直线CP相交所成的较小角的度数是.

（2）类比探究
如图2，当 $\text{[math]}$ 时，请写出 $\text{[math]}$ 的值及直线BD与直线CP相交所成的小角的度数，并就图2的情形说明理由.

（3）解决问题
当 $\text{[math]}$ 时，若点E，F分别是CA，CB的中点，点P在直线EF上，请直接写出点C，P，D在同一直线上时 $\text{[math]}$ 的值.

查看解析收藏纠错

+选题
35. 如图，在菱形 $\text{[math]}$ 中， $\text{[math]}$ ，将边 $\text{[math]}$ 绕点 $\text{[math]}$ 逆时针旋转至 $\text{[math]}$ ，记旋转角为 $\text{[math]}$ ．过点 $\text{[math]}$ 作 $\text{[math]}$ 于点 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ $\text{[math]}$ 直线 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ ．

（1）（探索发现）
填空：当 $\text{[math]}$ 时， $\text{[math]}$ = $\text{[math]}$ ． $\text{[math]}$ 的值是

（2）（验证猜想）
当 $\text{[math]}$ 时，（1）中的结论是否仍然成立?若成立，请仅就图2的情形进行证明；若不成立，请说明理由；

（3）（拓展应用）
在（2）的条件下，若 $\text{[math]}$ ，当 $\text{[math]}$ 是等腰直角三角形时，请直接写出线段 $\text{[math]}$ 的长．

查看解析收藏纠错

+选题
36. 在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点P是平面内不与点A，C重合的任意一点，连接CP，将线段CP绕点P旋转 $\text{[math]}$ 得到线段DP，连结AP，CD，BD.

（1）观察猜想：如图1，当 $\text{[math]}$ 时，线段CP绕点P顺时针旋转 $\text{[math]}$ 得到线段DP，则 $\text{[math]}$ 的值是，直线AP与BD相交所成的较小角的度数是；

（2）类比探究：如图2，当 $\text{[math]}$ 时，线段CP绕点P顺时针旋转 $\text{[math]}$ 得到线段 $\text{[math]}$ 请直接写出AP与BD相交所成的较小角的度数，并说明 $\text{[math]}$ 与 $\text{[math]}$ 相似，求出 $\text{[math]}$ 的值；

（3）拓展延伸：当 $\text{[math]}$ 时，且点P到点C的距离为 $\text{[math]}$ ，线段CP绕点P逆时针旋转 $\text{[math]}$ 得到线段DP，若点A，C，P在一条直线上时，求 $\text{[math]}$ 的值.

查看解析收藏纠错

+选题
37. 如图①，△ABC为直角三角形，∠ACB＝90°，∠BAC＝30°，点D在AB边上，过点D作DE⊥AC于点E，取BC边的中点F，连接DF并延长到点G，使FG＝DF，连接CG.（如需作图或作辅助线，请先将原题草图画在对应题目的答题区域后再作答.）

（1）问题发现：
填空：CE与CG的数量关系是，直线CE与CG所夹的锐角的度数为.

（2）探究证明：
将△ADE绕点A逆时针旋转，（1）中的结论是否仍然成立，若成立，请仅就图②所示情况给出证明，若不成立，请说明理由；

（3）问题解决：
若AB＝4，AD＝3，将△ADE由图①位置绕点A逆时针旋转α（0°＜α＜180°），当△ACE是直角三角形时，请直接写出CG的值.

查看解析收藏纠错

+选题
38. 如图

（1）观察猜想：如图1，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 的平分线，以 $\text{[math]}$ 为一边作正方形 $\text{[math]}$ ，点 $\text{[math]}$ 与点 $\text{[math]}$ 重合，则 $\text{[math]}$ .

（2）类比探究：在（1）的条件下，如果正方形 $\text{[math]}$ 绕点 $\text{[math]}$ 旋转，连接 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ ，（1）中的结论是否成立？请按图2加以证明.

（3）问题解决：当正方形 $\text{[math]}$ 旋转到 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 三点共线时，请直接写出线段 $\text{[math]}$ 的长.

查看解析收藏纠错

+选题
39. 在△ABC中，∠ACB＝90°，AC＝BC＝2，D是射线BC上一动点，过点B作BE⊥AD，垂足为点E，交直线AC于点P.

（1）（问题发现）
如图①，若点D在BC的延长线上，试猜想AP，CD，BC之间的数量关系为；

（2）（类比探究）
如图②，若点D在线段BC上，试猜想AP，CD，BC之间的数量关系，并说明理由；

（3）（拓展应用）
当E为BP的中点时，直接写出线段CD的长度.

查看解析收藏纠错

+选题
40. 如图

（1）问题发现
如图①，△ABC和△CDE均为等边三角形，直线AD和直线BE交于点F.

填空：①∠AFB的度数是；

②线段AD，BE之间的数量关系为.

（2）类比探究
如图②，△ABC和△CDE均为等腰直角三角形，∠ABC＝∠DEC＝90°，AB＝BC，DE＝EC，直线AD和直线BE交于点F.请判断∠AFB的度数及线段AD，BE之间的数量关系，并说明理由.

（3）解决问题
如图③，在平面直角坐标系中，点A的坐标为(4，0)，点B为y轴上任意一点，连接AB，将BA绕点B逆时针旋转90°至BC，连接OC，请直接写出OC的最小值.

查看解析收藏纠错

+选题
41. 定义：长宽比为 $\text{[math]}$ ：1（n为正整数）的矩形称为 $\text{[math]}$ 矩形.
下面，我们通过折叠的方式折出一个 $\text{[math]}$ 矩形，如图a所示.

操作1：将正方形ABEF沿过点A的直线折叠，使折叠后的点B落在对角线AE上的点G处，折痕为AH.

操作2：将FE沿过点G的直线折叠，使点F、点E分别落在边AF，BE上，折痕为CD.则四边形ABCD为 $\text{[math]}$ 矩形.

（1）证明：四边形ABCD为 $\text{[math]}$ 矩形；

（2）点M是边AB上一动点.
①如图b，O是对角线AC的中点，若点N在边BC上，OM⊥ON，连接MN.求tan∠OMN的值；

②若AM=AD，点N在边BC上，当△DMN的周长最小时，求 $\text{[math]}$ 的值；

③连接CM，作BR⊥CM，垂足为R.若AB=2 $\text{[math]}$ ，则DR的最小值= .

查看解析收藏纠错

+选题

河南省中考数学真题模拟题分类卷5 图形的变换及锐角三角函数（近几年）

一、单选题

二、填空题

三、解答题

四、综合题

相关试卷 收起∨

相关试卷收起∨