修改时间:2021-09-29 浏览次数:166 类型:二轮复习
该地区每周接种疫苗人数统计表
|
周次 |
第1周 |
第2周 |
第3周 |
第4周 |
第5周 |
第6周 |
第7周 |
第8周 |
|
接种人数(万人) |
7 |
10 |
12 |
18 |
25 |
29 |
37 |
42 |
|
该地区全民接种疫苗情况扇形统计图 | A:建议接种疫苗已接种人群 B:建议接种疫苗尚未接种人群 C:暂不建议接种疫苗人群 | |||||||
根据统计表中的数据,建立以周次为横坐标,接种人数为纵坐标的平面直角坐标系,并根据以上统计表中的数据描出对应的点,发现从第3周开始这些点大致分布在一条直线附近,现过其中两点 、
作一条直线(如图所示,该直线的函数表达式为
),那么这条直线可近似反映该地区接种人数的变化趋势.
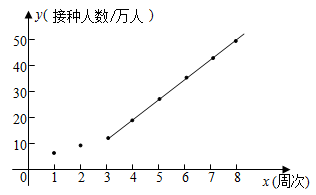
请根据以上信息,解答下列问题:
①估计第9周的接种人数约为 ▲ 万人;
②专家表示:疫苗接种率至少达60%,才能实现全民免疫.那么,从推广疫苗接种工作开始,最早到第几周,该地区可达到实现全民免疫的标准?
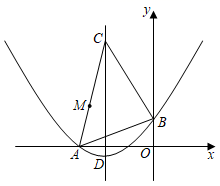
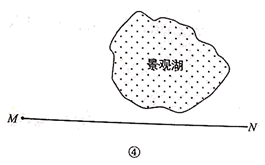
①请作出图中点M的对应点N和折痕所在直线l;(要求:尺规作图,不写作法,保留作图痕迹)
②连接MP,NP,在下列选项中:A.折痕与AB垂直,B.折痕与MN的交点可以落在抛物线的对称轴上,C. =
,D.
=
,所有正确选项的序号是 .
③点Q在二次函数y=ax2+bx+c(a≠0)的图象上,当 PDQ∼
PMN时,求点Q的坐标.
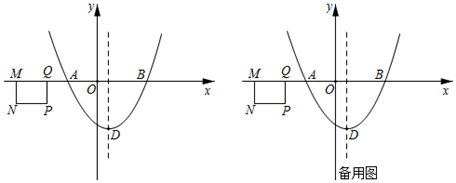
Ⅰ.在 中,
,在探究三边关系时,通过画图,度量和计算,收集到,组数据如下表:(单位:厘米)
| | 2.8 | 2.7 | 2.6 | 2.3 | 2 | 1.5 | 0.4 |
| | 0.4 | 0.8 | 1.2 | 1.6 | 2 | 2.4 | 2.8 |
| | 3.2 | 3.5 | 3.8 | 3.9 | 4 | 3.9 | 3.2 |
Ⅱ.根据学习函数的经验,选取上表中 和
的数据进行分析;
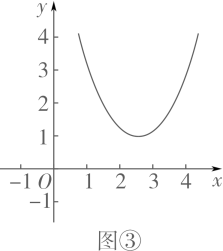
设
,以
为坐标,在图
所示的坐标系中描出对应的点;
连线;
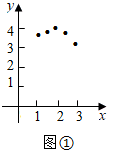
Ⅲ.观察思考
结合表中的数据以及所面的图像,猜想.当 ▲ 时,y最大;
Ⅳ.进一步C猜想:若 中,
,斜边
为常数,
),则
▲ 时,
最大.
推理证明
Ⅴ.对(4)中的猜想进行证明.

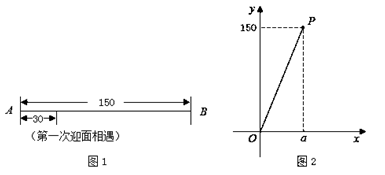
①观察图 ,若这两个机器人第一次迎面相遇时,相遇地点与点
之间的距离为
个单位长度,则他们第二次迎面相遇时,相遇地点与点
之间的距离为 个单位长度;
②若这两个机器人第一次迎面相遇时,相遇地点与点 之间的距离为
个单位长度,则他们第二次迎面相遇时,相遇地点与点
之间的距离为 个单位长度;
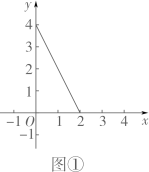
设这两个机器人第一次迎面相遇时,相遇地点与点 之间的距离为
个单位长度,他们第二次迎面相遇时,相遇地点与点
之间的距离为
个单位长度.兴趣小组成员发现了
与
的函数关系,并画出了部分函数图象(线段
,不包括点
,如图
所示).
① =;
②分别求出各部分图象对应的函数表达式,并在图 中补全函数图象;
设这两个机器人第一次迎面相遇时,相遇地点与点 之间的距离为
个单位长度,他们第三次迎面相遇时,相遇地点与点
之间的距离为
个单位长度.若这两个机器人第三次迎面相遇时,相遇地点与点
之间的距离
不超过
个单位长度,则他们第一次迎面相遇时,相遇地点与点
之间的距离
的取值范围是.(直接写出结果)
城市的许多街道是相互垂直或平行的,因此,往往不能沿直线行走到达目的地,只能按直角拐弯的方式行走.可以按照街道的垂直和平行方向建立平面直角坐标系xOy,对两点A( ,
)和B(
,
),用以下方式定义两点间距离:d(A,B)=
+
.

试题篮