全国历年中考数学真题精选汇编：反比例函数2

修改时间：2021-07-12 浏览次数：154 类型：二轮复习编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、单选题

1. 已知A（x₁ ， y₁）、B（x₂ ， y₂）、C（x₃ ， y₃）是反比例函数y= $\text{[math]}$ 上的三点，若x₁＜x₂＜x₃ ， y₂＜y₁＜y₃ ，则下列关系式不正确的是（　　）

A . x₁•x₂＜0 B . x₁•x₃＜0 C . x₂•x₃＜0 D . x₁+x₂＜0

查看解析收藏纠错

+选题
2. 已知某函数的图象C与函数y= $\text{[math]}$ 的图象关于直线y=2对称下列命题：①图象C与函数y= $\text{[math]}$ 的象交于点（ $\text{[math]}$ ，2）；②（ $\text{[math]}$ ，-2）在图象C上；③图象C上的点的纵坐标都小于4；④A（x₁ ， y₁），B（x₂ ， y₂）是图象C上任意两点，若x₁>x₂ ，则y₁-y₂ ，其中真命题是（）

A . ①② B . ①③④ C . ②③④ D . ①②③④

查看解析收藏纠错

+选题
3. 如图，平行于x轴的直线与函数 $\text{[math]}$ （k₁＞0，x＞0），y= $\text{[math]}$ （k₂＞0，x＞0）的图像分别交于A，B两点，点A在点B的右侧，C为x轴上的一个动点．若△ABC的面积为4，则k₁-k₂的值为（）

A . 8 B . -8 C . 4 D . -4

查看解析收藏纠错

+选题
4.
如图，已知在平面直角坐标系xOy中，O是坐标原点，点A是函数y= $\text{[math]}$ （x＜0）图象上一点，AO的延长线交函数y= $\text{[math]}$ （x＞0，k是不等于0的常数）的图象于点C，点A关于y轴的对称点为A′，点C关于x轴的对称点为C′，交于x轴于点B，连结AB，AA′，A′C′．若△ABC的面积等于6，则由线段AC，CC′，C′A′，A′A所围成的图形的面积等于（）

A . 8 B . 10 C . 3 $\text{[math]}$ D . 4 $\text{[math]}$

查看解析收藏纠错

+选题
5. 在平面直角坐标系中，分别过点A（m，0），B（m+2，0）作x轴的垂线l₁和l₂ ，探究直线l₁ ，直线l₂与双曲线y= $\text{[math]}$ 的关系，下列结论错误的是（）

A . 两直线中总有一条与双曲线相交 B . 当m=1时，两直线与双曲线的交点到原点的距离相等 C . 当﹣2＜m＜0时，两直线与双曲线的交点在y轴两侧 D . 当两直线与双曲线都有交点时，这两交点的最短距离是2

查看解析收藏纠错

+选题
6.
如图，在平面直角坐标系中，反比例函数y= $\text{[math]}$ （x＞0）的图象与边长是6的正方形OABC的两边AB，BC分别相交于M，N 两点，△OMN的面积为10．若动点P在x轴上，则PM+PN的最小值是（）

A . 6 $\text{[math]}$ B . 10 C . 2 $\text{[math]}$ D . 2 $\text{[math]}$

查看解析收藏纠错

+选题
7. 在平面直角坐标系内，直线AB垂直于x轴于点C（点C在原点的右侧），并分别与直线y=x和双曲线y= $\text{[math]}$ 相交于点A、B，且AC+BC=4，则△OAB的面积为（）

A . 2 $\text{[math]}$ +3或2 $\text{[math]}$ ﹣3 B . $\text{[math]}$ +1或 $\text{[math]}$ ﹣1 C . 2 $\text{[math]}$ ﹣3 D . $\text{[math]}$ ﹣1

查看解析收藏纠错

+选题
8.
如图，O为坐标原点，四边形OACB是菱形，OB在x轴的正半轴上，sin∠AOB= $\text{[math]}$ ，反比例函数y= $\text{[math]}$ 在第一象限内的图象经过点A，与BC交于点F，则△AOF的面积等于（　　）

A . 60 B . 80 C . 30 D . 40

查看解析收藏纠错

+选题
9.
如图，在Rt△AOB中，两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上，将△AOB绕点B逆时针旋转90°后得到△A′O′B．若反比例函数 $\text{[math]}$ 的图象恰好经过斜边A′B的中点C，S_△_ABO=4，tan∠BAO=2，则k的值为（　　）

A . 3 B . 4 C . 6 D . 8

查看解析收藏纠错

+选题
10.
如图，已知A，B是反比例函数y= $\text{[math]}$ （k＞0，x＞0）图象上的两点，BC∥x轴，交y轴于点C，动点P从坐标原点O出发，沿O→A→B→C（图中“→”所示路线）匀速运动，终点为C，过P作PM⊥x轴，垂足为M．设三角形OMP的面积为S，P点运动时间为t，则S关于x的函数图象大致为（　　）

A . B . C . D .

查看解析收藏纠错

+选题

二、填空题

11. 如图是8个台阶的示意图，每个台阶的高和宽分别是1和2，每个台阶凸出的角的顶点记作 $\text{[math]}$ （m为1~8的整数）．函数 $\text{[math]}$ （ $\text{[math]}$ ）的图象为曲线L．

（1）若L过点 $\text{[math]}$ ，则k=；

（2）若L过点 $\text{[math]}$ ，则它必定还过另一点 $\text{[math]}$ ，则m=；

（3）若曲线L使得 $\text{[math]}$ 这些点分布在它的两侧，每侧各4个点，则k的整数值有个．

查看解析收藏纠错

+选题
12. 如图，等腰 $\text{[math]}$ 的两个顶点 $\text{[math]}$ 、 $\text{[math]}$ 在反比例函数 $\text{[math]}$ （ $\text{[math]}$ ）的图象上， $\text{[math]}$ .过点C作边 $\text{[math]}$ 的垂线交反比例函数 $\text{[math]}$ （ $\text{[math]}$ ）的图象于点D，动点P从点D出发，沿射线 $\text{[math]}$ 方向运动 $\text{[math]}$ 个单位长度，到达反比例函数 $\text{[math]}$ （ $\text{[math]}$ ）图象上一点，则 $\text{[math]}$ .

查看解析收藏纠错

+选题
13. 如图，已知在平面直角坐标系xOy中，直线 $\text{[math]}$ 分别交x轴，y轴于点A和点B，分别交反比例函数 $\text{[math]}$ ， $\text{[math]}$ 的图象于点C和点D，过点C作CE⊥x轴于点E，连结OC，OD. 若△COE的面积与△DOB的面积相等，则k的值是.

查看解析收藏纠错

+选题
14. 已知△ABC的三个顶点为A $\text{[math]}$ ，B $\text{[math]}$ ，C $\text{[math]}$ ，将△ABC向右平移m（ $\text{[math]}$ ）个单位后，△ABC某一边的中点恰好落在反比例函数 $\text{[math]}$ 的图象上，则m的值为.

查看解析收藏纠错

+选题
15.
如图，一次函数y=﹣x+b与反比例函数y= $\text{[math]}$ （x＞0）的图象交于A，B两点，与x轴、y轴分别交于C，D两点，连结OA，OB，过A作AE⊥x轴于点E，交OB于点F，设点A的横坐标为m．

（1） b=（用含m的代数式表示）；

（2）若S_△_OAF+S_四边形_EFBC=4，则m的值是．

查看解析收藏纠错

+选题
16. 已知点P在一次函数y=kx+b（k，b为常数，且k＜0，b＞0）的图象上，将点P向左平移1个单位，再向上平移2个单位得到点Q，点Q也在该函数y=kx+b的图象上．

（1） k的值是；

（2）如图，该一次函数的图象分别与x轴、y轴交于A，B两点，且与反比例函数y= $\text{[math]}$ 图象交于C，D两点（点C在第二象限内），过点C作CE⊥x轴于点E，记S₁为四边形CEOB的面积，S₂为△OAB的面积，若 $\text{[math]}$ = $\text{[math]}$ ，则b的值是．

查看解析收藏纠错

+选题
17. 如图，在平面直角坐标系中，经过点A的双曲线y= $\text{[math]}$ （x＞0）同时经过点B，且点A在点B的左侧，点A的横坐标为 $\text{[math]}$ ，∠AOB=∠OBA=45°，则k的值为．

查看解析收藏纠错

+选题
18. 如图，已知菱形 $\text{[math]}$ 的对角线相交于坐标原点O，四个顶点分别在双曲线 $\text{[math]}$ 和 $\text{[math]}$ 上， $\text{[math]}$ .平行于x轴的直线与两双曲线分别交于点E，F，连接 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的面积为.

查看解析收藏纠错

+选题
19. 如图，AC⊥x轴于点A，点B在y轴的正半轴上，∠ABC=60°，AB=4，BC=2 $\text{[math]}$ ，点D为AC与反比例函数y= $\text{[math]}$ 的图象的交点．若直线BD将△ABC的面积分成1：2的两部分，则k的值为．

查看解析收藏纠错

+选题
20.
如图，OABC是平行四边形，对角线OB在轴正半轴上，位于第一象限的点A和第二象限的点C分别在双曲线y= $\text{[math]}$ 和y= $\text{[math]}$ 的一支上，分别过点A、C作x轴的垂线，垂足分别为M和N，则有以下的结论：
① $\text{[math]}$ = $\text{[math]}$ ；
②阴影部分面积是 $\text{[math]}$ （k₁+k₂）；
③当∠AOC=90°时，|k₁|=|k₂|；
④若OABC是菱形，则两双曲线既关于x轴对称，也关于y轴对称．
其中正确的结论是（把所有正确的结论的序号都填上）．

查看解析收藏纠错

+选题

三、综合题

21. 已知一次函数 $\text{[math]}$ 和反比例函数 $\text{[math]}$ ．

（1）如图1，若 $\text{[math]}$ ，且函数 $\text{[math]}$ 、 $\text{[math]}$ 的图象都经过点 $\text{[math]}$ ．
①求 $\text{[math]}$ ， $\text{[math]}$ 的值；

②直接写出当 $\text{[math]}$ 时 $\text{[math]}$ 的范围；

（2）如图2，过点 $\text{[math]}$ 作 $\text{[math]}$ 轴的平行线 $\text{[math]}$ 与函数 $\text{[math]}$ 的图象相交于点 $\text{[math]}$ ，与反比例函数 $\text{[math]}$ 的图象相交于点 $\text{[math]}$ ．
①若 $\text{[math]}$ ，直线 $\text{[math]}$ 与函数 $\text{[math]}$ 的图象相交点 $\text{[math]}$ ．当点 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 中的一点到另外两点的距离相等时，求 $\text{[math]}$ 的值；

②过点 $\text{[math]}$ 作 $\text{[math]}$ 轴的平行线与函数 $\text{[math]}$ 的图象相交于点 $\text{[math]}$ ．当 $\text{[math]}$ 的值取不大于1的任意实数时，点 $\text{[math]}$ 、 $\text{[math]}$ 间的距离与点 $\text{[math]}$ 、 $\text{[math]}$ 间的距离之和 $\text{[math]}$ 始终是一个定值．求此时 $\text{[math]}$ 的值及定值 $\text{[math]}$ ．

查看解析收藏纠错

+选题
22. 如图1，一次函数y=﹣x+b与反比例函数y= $\text{[math]}$ （k≠0）的图象交于点A（1，3），B（m，1），与x轴交于点D，直线OA与反比例函数y= $\text{[math]}$ （k≠0）的图象的另一支交于点C，过点B作直线l垂直于x轴，点E是点D关于直线l的对称点．

（1） k=；

（2）判断点B，E，C是否在同一条直线上，并说明理由；

（3）如图2，已知点F在x轴正半轴上，OF= $\text{[math]}$ ，点P是反比例函数y= $\text{[math]}$ （k≠0）的图象位于第一象限部分上的点（点P在点A的上方），∠ABP=∠EBF，则点P的坐标为（，）．

查看解析收藏纠错

+选题
23. 如图，在平面直角坐标系中，正次边形ABCDEF的对称中心P在反比例函数y= $\text{[math]}$ （k＞0，x>0）的图象上，边CD在x轴上，点B在y轴上，已知CD=2．

（1）点A是否在该反比例函数的图象上？请说明理曲。

（2）若该反比例函数图象与DE交于点Q，求点Q的横坐标。

（3）平移正六边形ABCDEF，使其一边的两个端点恰好都落在该反比例函数的图象上，试描述平移过程。

查看解析收藏纠错

+选题
24.
如图，点P是反比例函数y= $\text{[math]}$ （k＜0）图象上的点，PA垂直x轴于点A（﹣1，0），点C的坐标为（1，0），PC交y轴于点B，连结AB，已知AB= $\text{[math]}$ ．

（1） k的值是；

（2）若M（a，b）是该反比例函数图象上的点，且满足∠MBA＜∠ABC，则a的取值范围是．

查看解析收藏纠错

+选题
25.
如图，反比例函数y= $\text{[math]}$ 的图象经过点（﹣1，﹣2 $\text{[math]}$ ），点A是该图象第一象限分支上的动点，连结AO并延长交另一分支于点B，以AB为斜边作等腰直角三角形ABC，顶点C在第四象限，AC与x轴交于点P，连结BP．

（1） k的值为．

（2）在点A运动过程中，当BP平分∠ABC时，点C的坐标是．

查看解析收藏纠错

+选题
26.

【合作学习】

如图，矩形ABOD的两边OB，OD都在坐标轴的正半轴上，OD=3，另两边与反比例函数y= $\text{[math]}$ （k≠0）的图象分别相交于点E，F，且DE=2．过点E作EH⊥x轴于点H，过点F作FG⊥EH于点G．回答下面的问题：
①该反比例函数的解析式是什么？
②当四边形AEGF为正方形时，点F的坐标是多少？

（1）阅读合作学习内容，请解答其中的问题；

（2）小亮进一步研究四边形AEGF的特征后提出问题：“当AE＞EG时，矩形AEGF与矩形DOHE能否全等？能否相似？”
针对小亮提出的问题，请你判断这两个矩形能否全等？直接写出结论即可；这两个矩形能否相似？若能相似，求出相似比；若不能相似，试说明理由．

查看解析收藏纠错

+选题
27.
如图①，O为坐标原点，点B在x轴的正半轴上，四边形OACB是平行四边形，sin∠AOB= $\text{[math]}$ ，反比例函数y= $\text{[math]}$ （k＞0）在第一象限内的图象经过点A，与BC交于点F．

（1）若OA=10，求反比例函数解析式；

（2）若点F为BC的中点，且△AOF的面积S=12，求OA的长和点C的坐标；

（3）在（2）中的条件下，过点F作EF∥OB，交OA于点E（如图②），点P为直线EF上的一个动点，连接PA，PO．是否存在这样的点P，使以P、O、A为顶点的三角形是直角三角形？若存在，请直接写出所有点P的坐标；若不存在，请说明理由．

查看解析收藏纠错

+选题
28. 如图，点P为函数y＝ $\text{[math]}$ x+1与函数y＝ $\text{[math]}$ （x＞0）图象的交点，点P的纵坐标为4，PB⊥x轴，垂足为点B ．

（1）求m的值；

（2）点M是函数y＝ $\text{[math]}$ （x＞0）图象上一动点，过点M作MD⊥BP于点D ，若tan∠PMD＝ $\text{[math]}$ ，求点M的坐标．

查看解析收藏纠错

+选题
29.
定义：点P是△ABC内部或边上的点（顶点除外），在△PAB，△PBC，△PCA中，若至少有一个三角形与△ABC相似，则称点P是△ABC的自相似点.
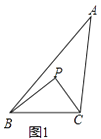
例如：如图1，点P在△ABC的内部，∠PBC=∠A，∠PCB=∠ABC，则△BCP∽△ABC，故点P是△ABC的自相似点.
请你运用所学知识，结合上述材料，解决下列问题：
在平面直角坐标系中，点M是曲线y= $\text{[math]}$ （x＞0）上的任意一点，点N是x轴正半轴上的任意一点.

（1）
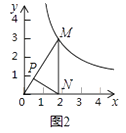
如图2，点P是OM上一点，∠ONP=∠M，试说明点P是△MON的自相似点；当点M的坐标是（ $\text{[math]}$ ，3），点N的坐标是（ $\text{[math]}$ ，0）时，求点P的坐标；

（2）
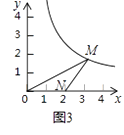
如图3，当点M的坐标是（3， $\text{[math]}$ ），点N的坐标是（2，0）时，求△MON的自相似点的坐标；

（3）是否存在点M和点N，使△MON无自相似点？若存在，请直接写出这两点的坐标；若不存在，请说明理由.

查看解析收藏纠错

+选题
30.
有这样一个问题：探究同一平面直角坐标系中系数互为倒数的正、反比例函数y= $\text{[math]}$ x与y= $\text{[math]}$ （k≠0）的图象性质．
小明根据学习函数的经验，对函数y= $\text{[math]}$ x与y= $\text{[math]}$ ，当k＞0时的图象性质进行了探究．
下面是小明的探究过程：

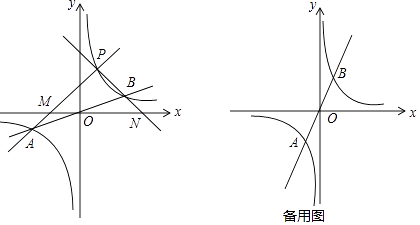
（1）如图所示，设函数y= $\text{[math]}$ x与y= $\text{[math]}$ 图象的交点为A，B，已知A点的坐标为（﹣k，﹣1），则B点的坐标为；

（2）若点P为第一象限内双曲线上不同于点B的任意一点．
①设直线PA交x轴于点M，直线PB交x轴于点N．求证：PM=PN．
证明过程如下，设P（m， $\text{[math]}$ ），直线PA的解析式为y=ax+b（a≠0）．
则 $\text{[math]}$ ，
解得 $\text{[math]}$
∴直线PA的解析式为 $\text{[math]}$
请你把上面的解答过程补充完整，并完成剩余的证明．
②当P点坐标为（1，k）（k≠1）时，判断△PAB的形状，并用k表示出△PAB的面积．

查看解析收藏纠错

+选题
31. 如图，一次函数y=kx+b与反比例函数y= $\text{[math]}$ 的图象在第一象限交于A、B两点，B点的坐标为（3，2），连接OA、OB，过B作BD⊥y轴，垂足为D，交OA于C，若OC=CA．

（1）求一次函数和反比例函数的表达式；

（2）求△AOB的面积．

查看解析收藏纠错

+选题
32. 如图，直线 $\text{[math]}$ 与反比例函数 $\text{[math]}$ 的图象交于A，B两点，已知点A的坐标为 $\text{[math]}$ ， $\text{[math]}$ 的面积为8.

（1）填空：反比例函数的关系式为；

（2）求直线 $\text{[math]}$ 的函数关系式；

（3）动点P在y轴上运动，当线段 $\text{[math]}$ 与 $\text{[math]}$ 之差最大时，求点P的坐标.

查看解析收藏纠错

+选题
33. 如图，直线y=2x+4与反比例函数y= $\text{[math]}$ 的图象相交于A（﹣3，a）和B两点

（1）求k的值；

（2）直线y=m（m＞0）与直线AB相交于点M，与反比例函数的图象相交于点N．若MN=4，求m的值；

（3）直接写出不等式 $\text{[math]}$ ＞x的解集．

查看解析收藏纠错

+选题
34. 如图，已知函数 $\text{[math]}$ 的图象与一次函数 $\text{[math]}$ 的图象相交不同的点A、B，过点A作AD⊥ $\text{[math]}$ 轴于点D，连接AO，其中点A的横坐标为 $\text{[math]}$ ，△AOD的面积为2.

（1）求 $\text{[math]}$ 的值及 $\text{[math]}$ =4时 $\text{[math]}$ 的值；

（2）记 $\text{[math]}$ 表示为不超过 $\text{[math]}$ 的最大整数，例如： $\text{[math]}$ ， $\text{[math]}$ ，设 $\text{[math]}$ ，若 $\text{[math]}$ ，求 $\text{[math]}$ 值

查看解析收藏纠错

+选题
35.
如图，一次函数y=k₁x+5（k₁＜0）的图象与坐标轴交于A，B两点，与反比例函数y= $\text{[math]}$ （k₂＞0）的图象交于M，N两点，过点M作MC⊥y轴于点C，已知CM=1．

（1）求k₂﹣k₁的值；

（2）若 $\text{[math]}$ = $\text{[math]}$ ，求反比例函数的解析式；

（3）在（2）的条件下，设点P是x轴（除原点O外）上一点，将线段CP绕点P按顺时针或逆时针旋转90°得到线段PQ，当点P滑动时，点Q能否在反比例函数的图象上？如果能，求出所有的点Q的坐标；如果不能，请说明理由．

查看解析收藏纠错

+选题
36.
如图，在平面直角坐标系中，一次函数的图象与反比例函数的图象交于第二、四象限内的A，B两点，与x轴交于点C，与y轴交于点D，点B的坐标是（m，﹣4），连接AO，AO=5，sin∠AOC= $\text{[math]}$ ．

（1）求反比例函数的解析式；

（2）连接OB，求△AOB的面积．

查看解析收藏纠错

+选题
37. 如图，一次函数y=ax+b的图象与反比例函数y= $\text{[math]}$ 的图象交于C，D两点，与x，y轴交于B，A两点，且tan∠ABO= $\text{[math]}$ ，OB=4，OE=2．

（1）求一次函数的解析式和反比例函数的解析式；

（2）求△OCD的面积；

（3）根据图象直接写出一次函数的值大于反比例函数的值时，自变量x的取值范围．

查看解析收藏纠错

+选题
38. 如图，设反比例函数的解析式为y= $\text{[math]}$ （k＞0）．

（1）若该反比例函数与正比例函数y=2x的图象有一个交点的纵坐标为2，求k的值；

（2）若该反比例函数与过点M（﹣2，0）的直线l：y=kx+b的图象交于A，B两点，如图所示，当△ABO的面积为 $\text{[math]}$ 时，求直线l的解析式．

查看解析收藏纠错

+选题

全国历年中考数学真题精选汇编：反比例函数2

一、单选题

二、填空题

三、综合题

相关试卷 收起∨

相关试卷收起∨