备考2022届中考数学全国精选题汇编专题7 函数知识的实际应用（2）

修改时间：2022-02-21 浏览次数：182 类型：一轮复习编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、综合题

1. 为响应吴兴区“千里助力，精准扶贫”活动，某销售平台为青川农户销售农产品，平台销售农产品的总运营成本为4元/千克，在销售过程中要保证农户的售价不低于7元/千克，且不超过15元/千克．如图记录了某三周的销售数据，经调查分析发现，每周的农产品销售量y（千克）与售价x（元/千克）（x为正整数）近似满足如图规律的函数关系.

（1）试写出y与x符合的函数表达式．

（2）若要确保农产品一周的销售量不少于6500千克，问：当农产品售价定为多少时，青川农户可获得最大收入？最大收入为多少？

查看解析收藏纠错

+选题
2. 我市绿色和特色农产品在国际市场上颇具竞争力，其中香菇远销日本和韩国等地.上市时，外贸商李经理按市场价格10元/千克在我市收购了2000千克香菇存放入冷库中.请根据李经理提供的预测信息（如下图）帮李经理解决以下问题：

（1）若存放 $\text{[math]}$ 天后，将这批香菇一次性出售，设这批香菇的销售总金额为 $\text{[math]}$ 元，试写出 $\text{[math]}$ 与 $\text{[math]}$ 之间的函数表达式；（销售总金额=销售单价×销售量）

（2）将这批香菇仔放多少天后出售可获得最大利润?最大利润是多少?

查看解析收藏纠错

+选题
3. 如图，钢球（不计大小）在一个光滑的“V”型轨道上滚动，其中右侧轨道长为25 m，左侧轨道长为30 m. 钢球先由静止开始沿右侧斜面滚下，速度每秒增加8m/s，到达底端后又沿着左侧斜面向上滚动，速度每秒减少am/s.
（提示：钢球滚动的距离=平均速度 $\text{[math]}$ ×时间t， $\text{[math]}$ = $\text{[math]}$ ，其中v₀表示开始的速度，v_t表示t秒时的速度.）

（1）若钢球在右侧轨道滚动2 s，则v_t=m/s， $\text{[math]}$ =m/s；

（2）写出钢球在右侧斜面滚动的距离S（单位：m）与时间t（单位：s）之间的函数解析式，并求出t的取值范围；

（3）若钢球滚出左侧斜面，直接写出a的取值范围.

查看解析收藏纠错

+选题
4. 某食品企业经调查发现，该企业生产的零食礼包的周销售量y（单位：万包）和售价x（单位：元/包）成一次函数的关系，其售价与周销售量的对应值如表所示：
售价x/（元/包）
20
19
18
周销售量y/万包
70
90
110

（1）求出y与x的函数关系式．

（2）若该零食礼包的生产成本是10.5元/包，则当每包的售价是多少元时，周销售利润最大？最大周销售利润是多少万元？此时周销售量是多少？

（3）在（2）条件下，该企业有A、B两种生产线若干条合作生产这种零食礼包，平均每条A种生产线每周可生产5万包，平均每条B种生产线每周可生产8万包，同时开通A、B两种生产线各多少条（数量均为整数），能够用一周的时间恰好生产出最大周销售利润时的周销售量？请直接写出使用A，B两种生产线数量之和最少的生产方案．

查看解析收藏纠错

+选题
5. 我市某卖场的一专营柜台，专营一种电器，每台进价60元．调查发现，当销售价80元时，平均每月能售出1000台；当销售价每涨1元时，平均每月能少售出10台；该柜台每月还需要支出20000元的其它费用，为了防止不正当竞争，稳定市场，市物价局规定：“出售时不得低于80元/台，又不得高于180元/台”．设售价为 $\text{[math]}$ 元/台时，月平均销售量为y台，月平均利润为w元．
注：月利润=月总售价-月总进价-其它费用，或月利润=月总销售量×单台利润-其它费用．

（1）当 $\text{[math]}$ 元/台时， $\text{[math]}$ 台， $\text{[math]}$ 元；

（2）求y与x的函数关系式，w与x的函数关系式（写出x的取值范围）；

（3）每台售价多少元时，月销售利润最高，最高为多少元；

（4）因为新品快要上市了，卖场既要想使该种电器平均每月获利7000元，又想要减少库存，售价应定为多少元．

查看解析收藏纠错

+选题
6. 某企业投资100万元引进一条农产品加工生产线，若不计维修、保养费用，预计投产后每年可创利33万元，但使用8年后生产线报废该，生产线投产后，从第1年到第x年的维修、保养费用累计为y万元，且y＝ax²+bx，若第1年的维修、保养费为2万元，第2年的为4万元．

（1）求a的值；

（2）小敏同学依题意判断，这条生产线在第四年能收回投资款，并在报废前能盈利100万元．你认为这个判断符合题意吗？请说明理由．

查看解析收藏纠错

+选题
7. 2020年以来，新冠肺炎的蔓延促使世界各国在线教育用户规模不断增大.网络教师小李抓住时机，开始组建团队，制作面向 $\text{[math]}$ 、 $\text{[math]}$ 两个不同需求学生群体的微课视频.已知制作3个 $\text{[math]}$ 类微课和5个 $\text{[math]}$ 类微课需要4600元成本，制作5个 $\text{[math]}$ 类微课和10个 $\text{[math]}$ 类微课需要8500元成本.李老师又把做好的微课出售给某视频播放网站，每个 $\text{[math]}$ 类微课售价1500元，每个 $\text{[math]}$ 类微课售价1000元.该团队每天可以制作1个 $\text{[math]}$ 类微课或者1.5个 $\text{[math]}$ 类微课，且团队每月制作的 $\text{[math]}$ 类微课数不少于 $\text{[math]}$ 类微课数的2倍（注：每月制作的 $\text{[math]}$ 、 $\text{[math]}$ 两类微课的个数均为整数）.假设团队每月有22天制作微课，其中制作 $\text{[math]}$ 类微课 $\text{[math]}$ 天，制作 $\text{[math]}$ 、 $\text{[math]}$ 两类微课的月利润为 $\text{[math]}$ 元.

（1）求团队制作一个 $\text{[math]}$ 类微课和一个 $\text{[math]}$ 类微课的成本分别是多少元？

（2）求 $\text{[math]}$ 与 $\text{[math]}$ 之间的函数关系式，并写出 $\text{[math]}$ 的取值范围；

（3）每月制作 $\text{[math]}$ 类微课多少个时，该团队月利润 $\text{[math]}$ 最大，最大利润是多少元？

查看解析收藏纠错

+选题
8. 甲秀楼是贵阳市一张靓丽的名片.如图①，甲秀楼的桥拱截面 $\text{[math]}$ 可视为抛物线的一部分，在某一时刻，桥拱内的水面宽 $\text{[math]}$ ，桥拱顶点 $\text{[math]}$ 到水面的距离是 $\text{[math]}$ .

（1）按如图②所示建立平面直角坐标系，求桥拱部分抛物线的函数表达式；

（2）一只宽为 $\text{[math]}$ 的打捞船径直向桥驶来，当船驶到桥拱下方且距 $\text{[math]}$ 点 $\text{[math]}$ 时，桥下水位刚好在 $\text{[math]}$ 处.有一名身高 $\text{[math]}$ 的工人站立在打捞船正中间清理垃圾，他的头顶是否会触碰到桥拱，请说明理由（假设船底与水面齐平）；

（3）如图③，桥拱所在的函数图象是抛物线 $\text{[math]}$ ，该抛物线在 $\text{[math]}$ 轴下方部分与桥拱 $\text{[math]}$ 在平静水面中的倒影组成一个新函数图象.将新函数图象向右平移 $\text{[math]}$ 个单位长度，平移后的函数图象在 $\text{[math]}$ 时， $\text{[math]}$ 的值随 $\text{[math]}$ 值的增大而减小，结合函数图象，求 $\text{[math]}$ 的取值范围.

查看解析收藏纠错

+选题
9. 某工艺厂为商城制作甲、乙两种木制工艺品，甲种工艺品不少于400 件，乙种工艺品不少于680件.该厂家现准备购买 $\text{[math]}$ 、 $\text{[math]}$ 两类原木共150根用于工艺品制作，其中，1根 $\text{[math]}$ 类原木可制作甲种工艺品4件和乙种工艺品2件，1根 $\text{[math]}$ 类原木可制作甲种工艺品2件和乙种工艺品6件.

（1）该工艺厂购买 $\text{[math]}$ 类原木根数可以有哪些？

（2）若每件甲种工艺品可获得利润50元，每件乙种工艺品可获得利润80元，那么该工艺厂购买 $\text{[math]}$ 、 $\text{[math]}$ 两类原木各多少根时获得利润最大，最大利润是多少？

查看解析收藏纠错

+选题

10. 去年“抗疫”期间，某生产消毒液厂家响应政府号召，将成本价为6元/件的简装消毒液低价销售.为此当地政府决定给予其销售的这种消毒液按a元/件进行补贴，设某月销售价为x元/件，a与x之间满足关系式： $\text{[math]}$ ，下表是某4个月的销售记录.每月销售量 $\text{[math]}$ （万件）与该月销售价x（元/件）之间成一次函数关系 $\text{[math]}$ .

月份	…	二月	三月	四月	五月	…
销售价x（元件）	…	6	7	7.6	8.5	…
该月销售量y（万件）	…	30	20	14	5	…

（1）求y与x的函数关系式；

（2）当销售价为8元/件时，政府该月应付给厂家补贴多少万元？

（3）当销售价x定为多少时，该月纯收入最大？（纯收入=销售总金额-成本+政府当月补贴）

查看解析收藏纠错

+选题

11. 小刚和小亮两人沿着直线跑道都从甲地出发，沿着同一方向到达乙地，甲乙两地之间的距离是720米，先到乙地的人原地休息，已知小刚先从甲地出发4秒后，小亮从甲地出发，两人均保持匀速前行．第一次相遇后，保持原速跑一段时间，小刚突然加速，速度比原来增加了2米/秒，并保持这一速度跑到乙地（小刚加速过程忽略不计）．小刚与小亮两人的距离 $\text{[math]}$ （米）与小亮出发时间 $\text{[math]}$ （秒）之间的函数图象，如图所示．根据所给信息解决以下问题．

（1） $\text{[math]}$ ， $\text{[math]}$ ；

（2）求 $\text{[math]}$ 和 $\text{[math]}$ 所在直线的解析式；

（3）直接写出 $\text{[math]}$ 为何值时，两人相距30米．

查看解析收藏纠错

+选题
12. 某快递公司为了提高工作效率，计划购买 $\text{[math]}$ 、 $\text{[math]}$ 两种型号的机器人来搬运货物，已知每台 $\text{[math]}$ 型机器人比每台 $\text{[math]}$ 型机器人每天多搬运20吨，并且3台 $\text{[math]}$ 型机器人和2台 $\text{[math]}$ 型机器人每天共搬运货物460吨.

（1）求每台 $\text{[math]}$ 型机器人和每台 $\text{[math]}$ 型机器人每天分别微运货物多少吨？

（2）每台 $\text{[math]}$ 型机器人售价3万元，每台 $\text{[math]}$ 型机器人售价2万元，该公司计划采购 $\text{[math]}$ 、 $\text{[math]}$ 两种型号的机器人共20台，必须满足每天搬运的货物不低于1800吨，请根据以上要求，求出 $\text{[math]}$ 、 $\text{[math]}$ 两种机器人分别采购多少台时，所需费用最低﹖最低费用是多少？

查看解析收藏纠错

+选题
13. 为增加农民收入，助力乡村振兴.某驻村干部指导农户进行草莓种植和销售，已知草莓的种植成本为8元/千克，经市场调查发现，今年五一期间草莓的销售量y（千克）与销售单价x（元/千克）（8≤x≤40）满足的函数图象如图所示.

（1）根据图象信息，求y与x的函数关系式；

（2）求五一期间销售草莓获得的最大利润.

查看解析收藏纠错

+选题
14. 某超市经销一种商品，每件成本为50元.经市场调研，当该商品每件的销售价为60元时，每个月可销售300件，若每件的销售价每增加1元，则每个月的销售量将减少10件.设该商品每件的销售价为x元，每个月的销售量为y件.

（1）求y与x的函数表达式；

（2）当该商品每件的销售价为多少元时，每个月的销售利润最大？最大利润是多少？

查看解析收藏纠错

+选题
15. 猕猴嬉戏是王屋山景区的一大特色，猕猴玩偶非常畅销.小李在某网店选中 $\text{[math]}$ ， $\text{[math]}$ 两款猕猴玩偶，决定从该网店进货并销售.两款玩偶的进货价和销售价如下表：

类别

价格

$\text{[math]}$ 款玩偶

$\text{[math]}$ 款玩偶

进货价（元/个）

40

30

销售价（元/个）

56

45

（1）第一次小李用1100元购进了 $\text{[math]}$ ， $\text{[math]}$ 两款玩偶共30个，求两款玩偶各购进多少个；

（2）第二次小李进货时，网店规定 $\text{[math]}$ 款玩偶进货数量不得超过 $\text{[math]}$ 款玩偶进货数量的一半.小李计划购进两款玩偶共30个，应如何设计进货方案才能获得最大利润，最大利润是多少？

（3）小李第二次进货时采取了（2）中设计的方案，并且两次购进的玩偶全部售出，请从利润率的角度分析，对于小李来说哪一次更合算？
（注：利润率 $\text{[math]}$ ）

查看解析收藏纠错

+选题
16. 如图1是一座抛物线型拱桥侧面示意图.水面宽AB与桥长CD均为24m，在距离D点6米的E处，测得桥面到桥拱的距离EF为1.5m，以桥拱顶点O为原点，桥面为x轴建立平面直角坐标系.

（1）求桥拱项部O离水面的距离.

（2）如图2，桥面上方有3根高度均为4m的支柱CG，OH，DI，过相邻两根支柱顶端的钢缆呈形状相同的抛物线，其最低点到桥面距离为1m.
①求出其中一条钢缆抛物线的函数表达式.

②为庆祝节日，在钢缆和桥拱之间竖直装饰若干条彩带，求彩带长度的最小值.

查看解析收藏纠错

+选题
17. 某商场以每件20元的价格购进一种商品，规定这种商品每件售价不低于进价，又不高于38元，经市场调查发现：该商品每天的销售量y（件）与每件售价（元）之间符合一次函数关系，如图所示．

（1）求y与x之间的函数关系式；

（2）该商场销售这种商品要想每天获得600元的利润，每件商品的售价应定为多少元？

（3）设商场销售这种商品每天获利w（元），当每件商品的售价定为多少元时，每天销售利润最大？最大利润是多少？

查看解析收藏纠错

+选题
18. 某工厂生产并销售A ， B两种型号车床共14台，生产并销售1台A型车床可以获利10万元；如果生产并销售不超过4台B型车床，则每台B型车床可以获利17万元，如果超出4台B型车床，则每超出1台，每台B型车床获利将均减少1万元．设生产并销售B型车床 $\text{[math]}$ 台．

（1）当 $\text{[math]}$ 时，完成以下两个问题：
①请补全下面的表格：

A型

B型

车床数量/台

▲

$\text{[math]}$

每台车床获利/万元

10

▲

②若生产并销售B型车床比生产并销售A型车床获得的利润多70万元，问：生产并销售B型车床多少台？

（2）当0＜ $\text{[math]}$ ≤14时，设生产并销售A ， B两种型号车床获得的总利润为W万元，如何分配生产并销售A ， B两种车床的数量，使获得的总利润W最大？并求出最大利润．

查看解析收藏纠错

+选题
19. 在一次机器“猫”抓机器“鼠”的展演测试中，“鼠”先从起点出发，1min后，“猫”从同一起点出发去追“鼠”，抓住“鼠”并稍作停留后，“猫”抓着“鼠”沿原路返回“鼠”、“猫”距起点的距离 $\text{[math]}$ 与时间 $\text{[math]}$ 之间的关系如图所示.

（1）在“猫”追“鼠”的过程中，“猫”的平均速度与“鼠”的平均速度的差是 $\text{[math]}$ ；

（2）求 $\text{[math]}$ 的函数表达式；

（3）求“猫”从起点出发到返回至起点所用的时间.

查看解析收藏纠错

+选题
20. 某商贸公司购进某种商品的成本为20元/ $\text{[math]}$ ，经过市场调研发现，这种商品在未来40天的销售单价y（元/ $\text{[math]}$ ）与时间x（天）之间的函数关系式为： $\text{[math]}$ 且x为整数，且日销量 $\text{[math]}$ 与时间x（天）之间的变化规律符合一次函数关系，如下表：

时间x（天）

1

3

6

10

…

日销量 $\text{[math]}$

142

138

132

124

…

填空：

（1） m与x的函数关系为；

（2）哪一天的销售利润最大？最大日销售利润是多少？

（3）在实际销售的前20天中，公司决定每销售 $\text{[math]}$ 商品就捐赠n元利润（ $\text{[math]}$ ）给当地福利院，后发现：在前20天中，每天扣除捐赠后的日销售利润随时间x的增大而增大，求n的取值范围.

查看解析收藏纠错

+选题

21. 某超市从厂家购进A、B两种型号的水杯，两次购进水杯的情况如下表：

进货批次	A型水杯（个）	B型水杯（个）	总费用（元）
一	100	200	8000
二	200	300	13000

（1）求A、B两种型号的水杯进价各是多少元？

（2）在销售过程中，A型水杯因为物美价廉而更受消费者喜欢.为了增大B型水杯的销售量，超市决定对B型水杯进行降价销售，当销售价为44元时，每天可以售出20个，每降价1元，每天将多售出5个，请问超市应将B型水杯降价多少元时，每天售出B型水杯的利润达到最大？最大利润是多少？

（3）第三次进货用10000元钱购进这两种水杯，如果每销售出一个A型水杯可获利10元，售出一个B型水杯可获利9元，超市决定每售出一个A型水杯就为当地“新冠疫情防控”捐b元用于购买防控物资.若A、B两种型号的水杯在全部售出的情况下，捐款后所得的利润始终不变，此时b为多少？利润为多少？

查看解析收藏纠错

+选题

22. 甲、乙两人沿同一直道从A地去B地，甲比乙早 $\text{[math]}$ 出发，乙的速度是甲的2倍.在整个行程中，甲离A地的距离 $\text{[math]}$ （单位：m）与时间x（单位： $\text{[math]}$ ）之间的函数关系如图所示.

（1）在图中画出乙离A地的距离 $\text{[math]}$ （单位：m）与时间x之间的函数图；

（2）若甲比乙晚 $\text{[math]}$ 到达B地，求甲整个行程所用的时间.

查看解析收藏纠错

+选题

23. 某通讯公司就手机流量套餐推出三种方案，如下表：

	A方案	B方案	C方案
每月基本费用（元）	20	56	266
每月免费使用流量（兆）	1024	m	无限
超出后每兆收费（元）	n	n

A，B，C三种方案每月所需的费用y（元）与每月使用的流量x（兆）之间的函数关系如图所示.

（1）请直接写出m，n的值.

（2）在A方案中，当每月使用的流量不少于1024兆时，求每月所需的费用y（元）与每月使用的流量x（兆）之间的函数关系式.

（3）在这三种方案中，当每月使用的流量超过多少兆时，选择C方案最划算？

查看解析收藏纠错

+选题

24. I号无人机从海拔10m处出发，以10m/min的速度匀速上升，II号无人机从海拔30m处同时出发，以a（m/min）的速度匀速上升，经过5min两架无人机位于同一海拔高度b（m）.无人机海拔高度y（m）与时间x（min）的关系如图.两架无人机都上升了15min.

（1）求b的值及II号无人机海拔高度y（m）与时间x（min）的关系式.

（2）问无人机上升了多少时间，I号无人机比II号无人机高28米.

查看解析收藏纠错

+选题
25. 电子体重科读数直观又便于携带，为人们带来了方便.某综合实践活动小组设计了简易电子体重秤：制作一个装有踏板（踏板质量忽略不计）的可变电阻R₁ ， R₁与踏板上人的质量m之间的函数关系式为R₁＝km+b（其中k，b为常数，0≤m≤120），其图象如图1所示；图2的电路中，电源电压恒为8伏，定值电阻R₀的阻值为30欧，接通开关，人站上踏板，电压表显示的读数为U₀ ，该读数可以换算为人的质量m，
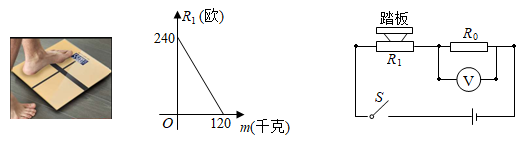
温馨提示：①导体两端的电压U，导体的电阻R，通过导体的电流I，满足关系式I＝ $\text{[math]}$ ；

②串联电路中电流处处相等，各电阻两端的电压之和等于总电压.

（1）求k，b的值；

（2）求R₁关于U₀的函数解析式；

（3）用含U₀的代数式表示m；

（4）若电压表量程为0~6伏，为保护电压表，请确定该电子体重秤可称的最大质量.

查看解析收藏纠错

+选题
26. 超市购进某种苹果，如果进价增加2元/千克要用300元；如果进价减少2元/千克，同样数量的苹果只用200元.

（1）求苹果的进价.

（2）如果购进这种苹果不超过100千克，就按原价购进；如果购进苹果超过100千克，超过部分购进价格减少2元/千克.写出购进苹果的支出y（元）与购进数量x（千克）之间的函数关系式.

（3）超市一天购进苹果数量不超过300千克，且购进苹果当天全部销售完.据统计，销售单价z（元/千克）与一天销售数量x（千克）的关系为 $\text{[math]}$ .在（2）的条件下，要使超市销售苹果利润w（元）最大，求一天购进苹果数量.（利润＝销售收入 $\text{[math]}$ 购进支出）

查看解析收藏纠错

+选题
27. 红星公司销售一种成本为40元/件的产品，若月销售单价不高于50元/件.一个月可售出5万件；月销售单价每涨价1元，月销售量就减少 $\text{[math]}$ 万件.其中月销售单价不低于成本.设月销售单价为x（单位：元/件），月销售量为y（单位：万件）.

（1）直接写出y与x之间的函数关系式，并写出自变量x的取值范围；

（2）当月销售单价是多少元/件时，月销售利润最大，最大利润是多少万元？

（3）为响应国家“乡村振兴”政策，该公司决定在某月每销售1件产品便向大别山区捐款a元.已知该公司捐款当月的月销售单价不高于70元/件，月销售最大利润是78万元，求a的值.

查看解析收藏纠错

+选题
28. 在“乡村振兴”行动中，某村办企业以 $\text{[math]}$ ， $\text{[math]}$ 两种农作物为原料开发了一种有机产品， $\text{[math]}$ 原料的单价是 $\text{[math]}$ 原料单价的1.5倍，若用900元收购 $\text{[math]}$ 原料会比用900元收购 $\text{[math]}$ 原料少 $\text{[math]}$ .生产该产品每盒需要 $\text{[math]}$ 原料 $\text{[math]}$ 和 $\text{[math]}$ 原料 $\text{[math]}$ ，每盒还需其他成本9元.市场调查发现：该产品每盒的售价是60元时，每天可以销售500盒；每涨价1元，每天少销售10盒.

（1）求每盒产品的成本（成本＝原料费＋其他成本）；

（2）设每盒产品的售价是 $\text{[math]}$ 元（ $\text{[math]}$ 是整数），每天的利润是 $\text{[math]}$ 元，求 $\text{[math]}$ 关于 $\text{[math]}$ 的函数解析式（不需要写出自变量的取值范围）；

（3）若每盒产品的售价不超过 $\text{[math]}$ 元（ $\text{[math]}$ 是大于60的常数，且是整数），直接写出每天的最大利润.

查看解析收藏纠错

+选题
29. 通过实验研究发现：初中生在数学课上听课注意力指标随上课时间的变化而变化，上课开始时，学生兴趣激增，中间一段时间，学生的兴趣保持平稳状态，随后开始分散.学生注意力指标y随时间x（分钟）变化的函数图象如图所示，当 $\text{[math]}$ 和 $\text{[math]}$ 时，图象是线段；当 $\text{[math]}$ 时，图象是反比例函数的一部分.

（1）求点A对应的指标值；

（2）张老师在一节课上讲解一道数学综合题需要17分钟，他能否经过适当的安排，使学生在听这道综合题的讲解时，注意力指标都不低于36？请说明理由.

查看解析收藏纠错

+选题
30. 疫苗接种，利国利民．甲、乙两地分别对本地各40万人接种新冠疫苗．甲地在前期完成5万人接种后，甲、乙两地同时以相同速度接种，甲地经过 $\text{[math]}$ 天后接种人数达到25万人，由于情况变化，接种速度放缓，结果100天完成接种任务，乙地80天完成接种任务，在某段时间内，甲、乙两地的接种人数 $\text{[math]}$ （万人）与各自接种时间 $\text{[math]}$ （天）之间的关系如图所示．

（1）直接写出乙地每天接种的人数及 $\text{[math]}$ 的值；

（2）当甲地接种速度放缓后，求 $\text{[math]}$ 关于 $\text{[math]}$ 的函数解析式，并写出自变量 $\text{[math]}$ 的取值范围；

（3）当乙地完成接种任务时，求甲地未接种疫苗的人数．

查看解析收藏纠错

+选题
31. 鄂尔多斯市某宾馆共有50个房间供游客居住，每间房价不低于200元且不超过320元、如果游客居住房间，宾馆需对每个房间每天支出20元的各种费用．已知每个房间定价x（元）和游客居住房间数y（间）符合一次函数关系，如图是y关于x的函数图象．

（1）求y与x之间的函数解析式，并写出自变量x的取值范围；

（2）当房价定为多少元时，宾馆利润最大？最大利润是多少元？

查看解析收藏纠错

+选题
32. 如图1，小刚家，学校、图书馆在同一条直线上，小刚骑自行车匀速从学校到图书馆，到达图书馆还完书后，再以相同的速度原路返回家中（上、下车时间忽略不计）.小刚离家的距离 $\text{[math]}$ 与他所用的时间 $\text{[math]}$ 的函数关系如图2所示.

（1）小刚家与学校的距离为 $\text{[math]}$ ，小刚骑自行车的速度为 $\text{[math]}$ ；

（2）求小刚从图书馆返回家的过程中， $\text{[math]}$ 与 $\text{[math]}$ 的函数表达式；

（3）小刚出发35分钟时，他离家有多远?

查看解析收藏纠错

+选题
33. 背景：点A在反比例函数 $\text{[math]}$ 的图象上， $\text{[math]}$ 轴于点B， $\text{[math]}$ 轴于点C，分别在射线 $\text{[math]}$ 上取点 $\text{[math]}$ ，使得四边形 $\text{[math]}$ 为正方形.如图1，点A在第一象限内，当 $\text{[math]}$ 时，小李测得 $\text{[math]}$ .
探究：通过改变点A的位置，小李发现点D，A的横坐标之间存在函数关系.请帮助小李解决下列问题.

（1）求k的值.

（2）设点 $\text{[math]}$ 的横坐标分别为 $\text{[math]}$ ，将z关于x的函数称为“Z函数”.如图2，小李画出了 $\text{[math]}$ 时“Z函数”的图象.
①求这个“Z函数”的表达式.

②补画 $\text{[math]}$ 时“Z函数”的图象，并写出这个函数的性质（两条即可）.

③过点 $\text{[math]}$ 作一直线，与这个“Z函数”图象仅有一个交点，求该交点的横坐标.

查看解析收藏纠错

+选题
34. 某游乐场的圆形喷水池中心O有一雕塑OA，从A点向四周喷水，喷出的水柱为抛物线，且形状相同.如图，以水平方向为x轴，点O为原点建立直角坐标系，点A在y轴上，x轴上的点C，D为水柱的落水点，水柱所在抛物线第一象限部分的函数表达式为 $\text{[math]}$ .

（1）求雕塑高OA.

（2）求落水点C，D之间的距离.

（3）若需要在OD上的点E处竖立雕塑EF， $\text{[math]}$ ， $\text{[math]}$ .问：顶部F是否会碰到水柱？请通过计算说明.

查看解析收藏纠错

+选题

	A型	B型
车床数量/台	▲	$\text{[math]}$
每台车床获利/万元	10	▲

时间x（天）	1	3	6	10	…
日销量 $\text{[math]}$	142	138	132	124	…

售价x/（元/包）	20	19	18
周销售量y/万包	70	90	110

备考2022届中考数学全国精选题汇编专题7 函数知识的实际应用（2）

一、综合题

相关试卷 收起∨

相关试卷收起∨