湘教版备考2021年中考数学二轮复习专题19反比例函数

1. 如图，正比例函数 $\text{[math]}$ 的图象与反比例函数 $\text{[math]}$ 的图象交于 $\text{[math]}$ ， $\text{[math]}$ 两点， $\text{[math]}$ ，两边分别交 $\text{[math]}$ 轴， $\text{[math]}$ 轴于点 $\text{[math]}$ ， $\text{[math]}$ ，四边形 $\text{[math]}$ 的面积为 $\text{[math]}$ ， $\text{[math]}$ 轴于点 $\text{[math]}$ .有下列结论：① $\text{[math]}$ ；②三角形 $\text{[math]}$ 的面积为 $\text{[math]}$ ；③线段 $\text{[math]}$ 的长为 $\text{[math]}$ ；④不等式 $\text{[math]}$ 的解集是 $\text{[math]}$ 或 $\text{[math]}$ .其中正确结论的个数是（）.

A . 1 B . 2 C . 3 D . 4

查看解析收藏纠错

+选题
2. 如图在平面直角坐标系中，直线 $\text{[math]}$ 分别与x轴、y轴交于点A、B ，与 $\text{[math]}$ 的图象交于点C、D ．若CD = $\text{[math]}$ AB ，则k的值为（）

A . $\text{[math]}$ ． B . $\text{[math]}$ ． C . $\text{[math]}$ ． D . $\text{[math]}$ ．

查看解析收藏纠错

+选题
3. 如图，直线l⊥x轴于点P ，且与反比例函数 $\text{[math]}$ ＝ $\text{[math]}$ （x＞0）及 $\text{[math]}$ ＝ $\text{[math]}$ （x＞0）的图象分别交于点A、B ，连接OA、OB ，若△OAB的面积为3，则k₁﹣k₂的值为（）

A . $\text{[math]}$ B . 3 C . 6 D . 9

查看解析收藏纠错

+选题
4. 我们知道，方程x²+2x-1=0的解可看作函数y=x+2的图象与函数y= $\text{[math]}$ 的图象交点的横坐标。那么方程kx²+x-4=0(k≠0)的两个解其实就是直线y=kx+1与双曲线y= $\text{[math]}$ 的图象交点的横坐标。若这两个交点所对应的坐标为(x₁ ， $\text{[math]}$ )、(x₂ ， $\text{[math]}$ )，且均在直线y=x的同侧，则实数k的取值范围是（）

A . $\text{[math]}$ <k< $\text{[math]}$ B . $\text{[math]}$ <k< $\text{[math]}$ C . $\text{[math]}$ <k<0或0<k< $\text{[math]}$ D . $\text{[math]}$ <k< $\text{[math]}$ 或 $\text{[math]}$ <k<0

查看解析收藏纠错

+选题
5. 如图，在平面直角坐标系中， $\text{[math]}$ 的顶点A在第一象限，顶点B在x轴的正半轴．函数 $\text{[math]}$ 经过 $\text{[math]}$ 的中点D，且与 $\text{[math]}$ 交于点C，则 $\text{[math]}$ 的值为（）．

A . $\text{[math]}$ B . 3 C . $\text{[math]}$ D . 4

查看解析收藏纠错

+选题
6. 已知点 $\text{[math]}$ ，点 $\text{[math]}$ 是函数 $\text{[math]}$ 上的一点，若 $\text{[math]}$ （O为坐标原点），则 $\text{[math]}$ 的面积为（）

A . 1 B . 2 C . 3 D . 4

查看解析收藏纠错

+选题
7. 平面直角坐标系中，函数y＝ $\text{[math]}$ （x＞0）的图象G经过点A（4，1），与直线y＝ $\text{[math]}$ x+b的图象交于点B ，与y轴交于点C ．其中横、纵坐标都是整数的点叫做整点．记图象G在点A、B之间的部分与线段OA、OC、BC围成的区域（不含边界）为W ．若W内恰有4个整点，结合函数图象，b的取值范围是（）

A . ﹣ $\text{[math]}$ ≤b＜1或 $\text{[math]}$ ＜b≤ $\text{[math]}$ B . ﹣ $\text{[math]}$ ≤b＜1或 $\text{[math]}$ ＜b≤ $\text{[math]}$ C . ﹣ $\text{[math]}$ ≤b＜﹣1或﹣ $\text{[math]}$ ＜b≤ $\text{[math]}$ D . ﹣ $\text{[math]}$ ≤b＜﹣1或 $\text{[math]}$ ＜b≤ $\text{[math]}$

查看解析收藏纠错

+选题
8. 如图，反比例函数 $\text{[math]}$ 的图象分别与矩形 $\text{[math]}$ 的边 $\text{[math]}$ ， $\text{[math]}$ 相交于点 $\text{[math]}$ ， $\text{[math]}$ ，与对角线 $\text{[math]}$ 交于点 $\text{[math]}$ ，以下结论：

①若 $\text{[math]}$ 与 $\text{[math]}$ 的面积和为2，则 $\text{[math]}$ ；

②若 $\text{[math]}$ 点坐标为 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ ；

③图中一定有 $\text{[math]}$ ；

④若点 $\text{[math]}$ 是 $\text{[math]}$ 的中点，且 $\text{[math]}$ ，则四边形 $\text{[math]}$ 的面积为18.

其中一定正确个数是（）

A . 1 B . 2 C . 3 D . 4

查看解析收藏纠错

+选题
9. 已知函数y= $\text{[math]}$ ，下列说法：
①函数图象分布在第一、三象限；②在每个象限内，y随x的增大而减小；③若A(x₁ ， y₁)、B(x₂ ， y₂)两点在该图象上，且x₁+x₂=0，则y₁=y₂。其中说法正确的个数是（）

A . 0 B . 1 C . 2 D . 3

查看解析收藏纠错

+选题
10. 如图，点A、B为直线y＝x上的两点，过A、B两点分别作y轴的平行线交双曲线 $\text{[math]}$ （x＞0）于点C、D两点.若BD＝2AC，则4OC²﹣OD²的值为（）

A . 5 B . 6 C . 7 D . 8

查看解析收藏纠错

+选题

11. 如图，分别过x轴上的点 $\text{[math]}$ 作x轴的垂线，与反比例函数 $\text{[math]}$ 图象的交点分别为 $\text{[math]}$ 与 $\text{[math]}$ 相交于点 $\text{[math]}$ 与 $\text{[math]}$ 相交于点 $\text{[math]}$ ，…， $\text{[math]}$ 与 $\text{[math]}$ 相交于点 $\text{[math]}$ ，若 $\text{[math]}$ 的面积记为 $\text{[math]}$ ， $\text{[math]}$ 的面积记为 $\text{[math]}$ ， $\text{[math]}$ 的面积记为 $\text{[math]}$ ，… $\text{[math]}$ 的面积记为 $\text{[math]}$ ，则 $\text{[math]}$ =

查看解析收藏纠错

+选题
12. 如图，经过原点的直线与反比例函数y= $\text{[math]}$ (k>0)相交于A，B两点，BC⊥x轴。若△ABC的面积为4，则k的值为。

查看解析收藏纠错

+选题
13. 如图是8个台阶的示意图，每个台阶的高和宽分别是1和2，每个台阶凸出的角的顶点记作 $\text{[math]}$ （m为1~8的整数）．函数 $\text{[math]}$ （ $\text{[math]}$ ）的图象为曲线L．

（1）若L过点 $\text{[math]}$ ，则k=；

（2）若L过点 $\text{[math]}$ ，则它必定还过另一点 $\text{[math]}$ ，则m=；

（3）若曲线L使得 $\text{[math]}$ 这些点分布在它的两侧，每侧各4个点，则k的整数值有个．

查看解析收藏纠错

+选题
14. 如图，等腰 $\text{[math]}$ 的两个顶点 $\text{[math]}$ 、 $\text{[math]}$ 在反比例函数 $\text{[math]}$ （ $\text{[math]}$ ）的图象上， $\text{[math]}$ .过点C作边 $\text{[math]}$ 的垂线交反比例函数 $\text{[math]}$ （ $\text{[math]}$ ）的图象于点D，动点P从点D出发，沿射线 $\text{[math]}$ 方向运动 $\text{[math]}$ 个单位长度，到达反比例函数 $\text{[math]}$ （ $\text{[math]}$ ）图象上一点，则 $\text{[math]}$ .

查看解析收藏纠错

+选题
15. 如图，已知菱形 $\text{[math]}$ 的对角线相交于坐标原点O，四个顶点分别在双曲线 $\text{[math]}$ 和 $\text{[math]}$ 上， $\text{[math]}$ .平行于x轴的直线与两双曲线分别交于点E，F，连接 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的面积为.

查看解析收藏纠错

+选题
16. 已知直线 $\text{[math]}$ 与反比例函数 $\text{[math]}$ 的图象交于A、B两点，当线段AB的长最小时，以AB为斜边作等腰直角三角形△ABC，则点C的坐标是．

查看解析收藏纠错

+选题
17. 如图，在平面直角坐标系中，菱形OABC的边OA在x轴的正半轴上，反比例函数y= $\text{[math]}$ (x>0)的图象经过对角线OB的中点D和顶点C。若菱形OABC的面积为6 $\text{[math]}$ ，则k=。

查看解析收藏纠错

+选题
18. 如图，点A、B在函数 $\text{[math]}$ ( $\text{[math]}$ ， $\text{[math]}$ 且 $\text{[math]}$ 是常数)的图象上，且点A在点B的左侧过点A作 $\text{[math]}$ 轴，垂足为M，过点B作 $\text{[math]}$ 轴，垂足为N， $\text{[math]}$ 与 $\text{[math]}$ 的交点为C，连结 $\text{[math]}$ 、 $\text{[math]}$ .若 $\text{[math]}$ 和 $\text{[math]}$ 的面积分别为1和4，则k的值为.

查看解析收藏纠错

+选题
19. 如图，已知△OAB中，AB⊥OB，以O为原点，以BO所在直线为x轴建立坐标系。反比例函数的图象分别交AO，AB于点C，D，已知 $\text{[math]}$ ，△ACD的面积为 $\text{[math]}$ ，则该反比例函数的解析式为。

查看解析收藏纠错

+选题
20. 如图，在平面直角坐标系中，Rt△AOB的直角顶点A在y轴的正半轴上，顶点B在第一象限，函数y= $\text{[math]}$ 的图象与边OB交于点C，并且点C为边OB的中点，若△AOB的面积为12，则k的值为。

查看解析收藏纠错

+选题

21. 如图，将一个∠B= $\text{[math]}$ 的直角三角形板的斜边 $\text{[math]}$ 放在 $\text{[math]}$ 轴上，直角顶点 $\text{[math]}$ 在反比例函数 $\text{[math]}$ 的图象上， $\text{[math]}$ ，求点 $\text{[math]}$ 的坐标．

查看解析收藏纠错

+选题
22. 如图，△PAB的直角顶点P在第四象限，顶点A、B分别落在反比例函数 $\text{[math]}$ 图象的两个分支上，且PB⊥x轴于点C，PA⊥y轴于点D，AB分别与x轴，y轴相交于点E、F已知B（1，3）

（1） k=；

（2）试说明AE=BF；

（3）当四边形ABCD的面积为 $\text{[math]}$ 时，求点P的坐标。

查看解析收藏纠错

+选题
23. 综合题

（1）
探究：如图1 ，直线l与坐标轴的正半轴分别交于A，B两点，与反比例函数 $\text{[math]}$ $\text{[math]}$ 的图象交于C，D两点(点C在点D的左边)，过点C作CE⊥y轴于点E，过点D作DF⊥x轴于点F，CE与DF交于点G(a ， b).
①若 $\text{[math]}$ ，请用含n的代数式表示 $\text{[math]}$ ；
②求证： $\text{[math]}$ ；

（2）
应用：如图2，直线l与坐标轴的正半轴分别交于点A，B两点，与反比例函数 $\text{[math]}$ $\text{[math]}$ 的图象交于点C，D两点(点C在点D的左边)，已知 $\text{[math]}$ ，△OBD的面积为1，试用含m的代数式表示k.

查看解析收藏纠错

+选题
24. 说明：在解答“结论应用”时，从A，B两题中任选一题作答.
问题探究：
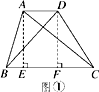
启知学习小组在课外学习时，发现了这样一个问题：如图①，在四边形ABCD中，连接AC，BD，如果△ABC与△BCD的面积相等，那么AD∥BC.在小组交流时，他们在图①中添加了如图所示的辅助线，AE⊥BC于点E，DF⊥BC于点F.请你完成他们的证明过程.
结论应用：
在平面直角坐标系中，反比例函数y= $\text{[math]}$ (x≠0)的图象经过A(1，4)，B(a，b)两点，过点A作AC⊥x轴于点C，过点B作BD⊥y轴于点D.

（1） A
Ⅰ.求反比例函数的表达式；
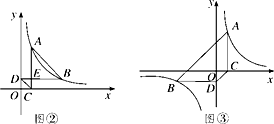
Ⅱ.如图②，已知b=1，AC，BD相交于点E，求证：CD∥AB.

（2） B
Ⅰ.求反比例函数的表达式；
Ⅱ.如图③，若点B在第三象限，判断并证明CD与AB的位置关系.

查看解析收藏纠错

+选题

25. 如图，一次函数 $\text{[math]}$ 与反比例函数 $\text{[math]}$ 的图象相交于 $\text{[math]}$ ， $\text{[math]}$ 两点，连接 $\text{[math]}$ ， $\text{[math]}$ ，延长 $\text{[math]}$ 交反比例函数图象于点 $\text{[math]}$ .

（1）求一次函数 $\text{[math]}$ 的表达式与反比例函数 $\text{[math]}$ 的表达式；

（2）当 $\text{[math]}$ 时，直接写出自变量 $\text{[math]}$ 的取值范围为；

（3）点 $\text{[math]}$ 是 $\text{[math]}$ 轴上一点，当 $\text{[math]}$ 时，请直接写出点 $\text{[math]}$ 的坐标为.

查看解析收藏纠错

+选题
26. 如图，一次函数 $\text{[math]}$ 的图象与反比例函数 $\text{[math]}$ 的图象交于 $\text{[math]}$ 两点.

（1）求这两个函数的表达式；

（2）求 $\text{[math]}$ 的面积；

（3）根据图象回答：当x取何值时，反比例函数的值大于一次函数的值.

查看解析收藏纠错

+选题
27. 如图，一次函数 $\text{[math]}$ 与反比例函数 $\text{[math]}$ 的图象交于点 $\text{[math]}$ 和 $\text{[math]}$ ，与y轴交于点C.

（1） $\text{[math]}$ =， $\text{[math]}$ =；

（2）根据函数图象可知，当 $\text{[math]}$ ＞ $\text{[math]}$ 时，x的取值范围是；

（3）过点A作AD⊥x轴于点D ，点P是反比例函数在第一象限的图象上一点.设直线OP与线段AD交于点E ，当 $\text{[math]}$ ： $\text{[math]}$ =3：1时，求点P的坐标.

查看解析收藏纠错

+选题
28. 如图，一次函数y₁=- $\text{[math]}$ x+3与反比例函数y₂= $\text{[math]}$ 的图象交于A、B两点，A点的横坐标为3。

（1）求反比例函数的解析式；

（2）结合图象，直接写出y₁<y₂时，x的取值范围。

查看解析收藏纠错

+选题
29. 如图，直线 $\text{[math]}$ 与反比例函数 $\text{[math]}$ 的图象交于A，B两点，已知点A的坐标为 $\text{[math]}$ ， $\text{[math]}$ 的面积为8.

（1）填空：反比例函数的关系式为；

（2）求直线 $\text{[math]}$ 的函数关系式；

（3）动点P在y轴上运动，当线段 $\text{[math]}$ 与 $\text{[math]}$ 之差最大时，求点P的坐标.

查看解析收藏纠错

+选题

湘教版备考2021年中考数学二轮复习专题19反比例函数

一、单选题

二、填空题

三、解答题

四、综合题

相关试卷收起∨

湘教版备考2021年中考数学二轮复习专题19反比例函数

一、单选题

二、填空题

三、解答题

四、综合题

相关试卷 收起∨

相关试卷收起∨