2023年中考数学探究性试题复习18 旋转

修改时间：2023-05-24 浏览次数：114 类型：三轮冲刺编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、综合题

1.

（1）综合与实践
问题情境：如图1，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， D，E分别是 $\text{[math]}$ ， $\text{[math]}$ 的中点，连接 $\text{[math]}$ ．
如图2，将 $\text{[math]}$ 绕着点C逆时针旋转 $\text{[math]}$ ，连接BE和 $\text{[math]}$ ，小明发现 $\text{[math]}$ ， $\text{[math]}$ ，请你证明该结论．

（2）猜想探究：
如图3，将 $\text{[math]}$ 绕着点C逆时针旋转 $\text{[math]}$ ，此时恰好有 $\text{[math]}$ ，连接 $\text{[math]}$ ，延长 $\text{[math]}$ ，交 $\text{[math]}$ 于点F，试猜想四边形 $\text{[math]}$ 的形状，并说明理由．
拓展探究：

（3）如图4，将 $\text{[math]}$ 绕着点C逆时针旋转 $\text{[math]}$ ，直接写出四边形 $\text{[math]}$ 的面积的最大值．

查看解析收藏纠错

+选题
2. 在 $\text{[math]}$ 和 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，用这两个直角三角形研究图形的变换.

（1）【翻折】如图1，将 $\text{[math]}$ 沿线段 $\text{[math]}$ 翻折，连接 $\text{[math]}$ ，下列对所得四边形 $\text{[math]}$ 的说法正确的是.
① $\text{[math]}$ 平分 $\text{[math]}$ 、 $\text{[math]}$ ， ② $\text{[math]}$ 、 $\text{[math]}$ 互相平分，③ $\text{[math]}$ ， ④ $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 四点共圆.

（2）【平移】
如图2，将 $\text{[math]}$ 沿线段 $\text{[math]}$ 向右平移，使 $\text{[math]}$ 点移到 $\text{[math]}$ 的中点，连接 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ ，请猜想四边形 $\text{[math]}$ 的形状，并说明理由.

（3）【旋转】如图3，将 $\text{[math]}$ 绕点 $\text{[math]}$ 逆时针方向旋转，使 $\text{[math]}$ ，连接 $\text{[math]}$ 、 $\text{[math]}$ ，则旋转角为°， $\text{[math]}$ cm.

查看解析收藏纠错

+选题
3. 在学习了图形的旋转知识后，数学兴趣小组的同学们又进一步对图形旋转前后的线段之间、角之间的关系进行了探究．
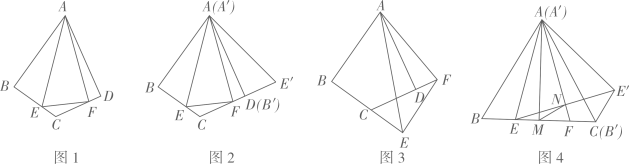
（一）尝试探究：如图1，在四边形ABCD中，AB＝AD，∠BAD＝60°，∠ABC＝∠ADC＝90°，点E、F分别在线段BC、CD上，∠EAF＝30°，连接EF．

（1）如图2，将△ABE绕点A逆时针旋转60°后得到△A′B′E′（A′B′与AD重合），请直接写出∠E′AF＝度，线段BE、EF、FD之间的数量关系为．

（2）如图3，当但点E、F分别在线段BC、CD的延长线上时，其他条件不变，请探究线段BE、EF、FD之间的数量关系，并说明理由．

（3）拓展延伸：如图4，在等边△ABC中，E、F是边BC上的两点，∠EAF＝30°，BE＝1，将△ABE绕点A逆时针旋转60°得到△A′B′E′（A′B′与AC重合），连接EE′，AF与EE′交于点N，过点A作AM⊥BC于点M，连接MN，求线段MN的长度．

查看解析收藏纠错

+选题
4. 如图

（1）问题发现：
如图1， $\text{[math]}$ 和 $\text{[math]}$ 都是等边三角形，边 $\text{[math]}$ 和 $\text{[math]}$ 在同一直线上， $\text{[math]}$ 是边 $\text{[math]}$ 的中点， $\text{[math]}$ ，连接 $\text{[math]}$ ，则下列结论正确的是．（填序号即可）
① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ ；④整个图形是轴对称图形．

（2）数学思考：将图1中的 $\text{[math]}$ 绕着点 $\text{[math]}$ 旋转， $\text{[math]}$ 不动，连接 $\text{[math]}$ 和 $\text{[math]}$ ，如图2，则 $\text{[math]}$ 和 $\text{[math]}$ 具有怎样的数量和位置关系？请给出证明过程；

（3）拓展应用：已知 $\text{[math]}$ ， $\text{[math]}$ ，在图1中的 $\text{[math]}$ 绕着点 $\text{[math]}$ 旋转的过程中，当 $\text{[math]}$ 时，求线段 $\text{[math]}$ 的长度．

查看解析收藏纠错

+选题
5. 在正方形 $\text{[math]}$ 中，点 $\text{[math]}$ 是对角线 $\text{[math]}$ 上的动点（与点 $\text{[math]}$ ， $\text{[math]}$ 不重合），连接 $\text{[math]}$ ．

（1）将射线 $\text{[math]}$ 绕点 $\text{[math]}$ 顺时针旋转 $\text{[math]}$ ，交直线 $\text{[math]}$ 于点 $\text{[math]}$ ．
①依题意补全图1；
②小深通过观察、实验，发现线段 $\text{[math]}$ 存在以下数量关系： $\text{[math]}$ 的平方和等于 $\text{[math]}$ 的平方．小深把这个猜想与同学们进行交流，通过讨论，形成证明该猜想的几种想法：
想法1：将线段 $\text{[math]}$ 绕点 $\text{[math]}$ 逆时针旋转 $\text{[math]}$ ，得到线段 $\text{[math]}$ ，要证 $\text{[math]}$ 的关系，只需证 $\text{[math]}$ 的关系．
想法2：将 $\text{[math]}$ 沿 $\text{[math]}$ 翻折，得到 $\text{[math]}$ ，要证 $\text{[math]}$ 的关系，只需证 $\text{[math]}$ 的关系．
…
请你参考上面的想法，用等式表示线段 $\text{[math]}$ 的数量关系并证明；（一种方法即可）

（2）如图2，若将直线 $\text{[math]}$ 绕点B顺时针旋转 $\text{[math]}$ ，交直线 $\text{[math]}$ 于点 $\text{[math]}$ ．若正方形边长为 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长．

查看解析收藏纠错

+选题
6.

（1）【问题初探】
如图1，等腰 $\text{[math]}$ 中， $\text{[math]}$ ，点 $\text{[math]}$ 为 $\text{[math]}$ 边一点，以 $\text{[math]}$ 为腰向下作等腰 $\text{[math]}$ ， $\text{[math]}$ ．连接 $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 为 $\text{[math]}$ 的中点，连接 $\text{[math]}$ ．猜想并证明线段 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系和位置关系．

（2）【深入探究】
在（1）的条件下，如图2，将等腰 $\text{[math]}$ 绕点 $\text{[math]}$ 旋转，上述结论是否仍然成立？若成立，请证明；若不成立，请说明理由．

（3）【拓展迁移】
如图3，等腰 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ．在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ．连接 $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 为 $\text{[math]}$ 的中点，连接 $\text{[math]}$ ．
$\text{[math]}$ 绕点 $\text{[math]}$ 旋转过程中，
①线段 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系为：；
②若 $\text{[math]}$ ， $\text{[math]}$ ，当点 $\text{[math]}$ 在等腰 $\text{[math]}$ 内部且 $\text{[math]}$ 的度数最大时，线段 $\text{[math]}$ 的长度为．

查看解析收藏纠错

+选题
7. 如图1，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点D、E分别在边AB， $\text{[math]}$ 上， $\text{[math]}$ ，连接DC，点M，P，N分别为DE，DC，BC的中点.

（1）观察猜想：图中，线段PM与PN的数量关系是，位置关系是；

（2）探究证明：把 $\text{[math]}$ 绕点A逆时针方向旋转到图2的位置，连接 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，判断 $\text{[math]}$ 的形状，并说明理由；

（3）拓展延伸：把 $\text{[math]}$ 绕点A在平面内自由旋转，若 $\text{[math]}$ ， $\text{[math]}$ ，请直接写出 $\text{[math]}$ 面积的最大值.

查看解析收藏纠错

+选题
8. 如图1，在 $\text{[math]}$ 中， $\text{[math]}$ ， D，E两点分别在 $\text{[math]}$ 上，且 $\text{[math]}$ ，将 $\text{[math]}$ 绕点A顺时针旋转，记旋转角为 $\text{[math]}$ ．

（1）问题发现当 $\text{[math]}$ 时，线段 $\text{[math]}$ 的数量关系是；

（2）拓展探究当 $\text{[math]}$ 时，（1）中的结论有无变化？请仅就图2的情形给出证明；

（3）问题解决设 $\text{[math]}$ ， $\text{[math]}$ 旋转至A，B，E三点共线时，直接写出线段 $\text{[math]}$ 的长．

查看解析收藏纠错

+选题
9. 如图1，点O在直线 $\text{[math]}$ 上，过点O引一条射线 $\text{[math]}$ ，使 $\text{[math]}$ ，将一个直角三角尺的直角顶点放在点O处，直角边 $\text{[math]}$ 在射线 $\text{[math]}$ 上，另一边 $\text{[math]}$ 在直线 $\text{[math]}$ 的下方.

【操作一】：将图1中的三角尺绕着点O以每秒 $\text{[math]}$ 的速度按顺时针方向旋转.当它完成旋转一周时停止，设旋转的时间为t秒.

（1） $\text{[math]}$ 的度数是，图1中与它互补的角是.

（2）三角尺旋转的度数可表示为（用含t的代数式表示）；当 $\text{[math]}$ 时， $\text{[math]}$ .

（3）【操作二】：如图2将一把直尺的一端点也放在点O处，另一端点E在射线 $\text{[math]}$ 上.如图3，在三角尺绕着点O以每秒 $\text{[math]}$ 的速度按顺时针方向旋转的同时，直尺也绕着点O以每秒 $\text{[math]}$ 的速度按顺时针方向旋转，当一方完成旋转一周时停止，另一方也停止旋转，设旋转的时间为t秒.
试探索：在三角尺与直尺旋转的过程中，当 $\text{[math]}$ ，是否存在某个时刻，使得 $\text{[math]}$ 与 $\text{[math]}$ 中其中一个角是另一个角的两倍？若存在，请求出所有满足题意的t的值；若不存在，请说明理由.

查看解析收藏纠错

+选题
10. 阅读下面材料.
小炎遇到这个一个问题：如图1，点E、F分别在正方形 $\text{[math]}$ 的边 $\text{[math]}$ 上， $\text{[math]}$ ，连接 $\text{[math]}$ ，则 $\text{[math]}$ ，试说明理由.
小炎是这样思考的：要想解决这个问题，首先应想办法将这些分散的线段相对集中，她先尝试了翻折、旋转、平移的方法，最后发现线段 $\text{[math]}$ 是共点并且相等的，于是找到解决问题的方法.她的方法是将 $\text{[math]}$ 绕着点A逆时针旋转90°得到 $\text{[math]}$ ，再利用全等的知识解决这个问题（如图2）.
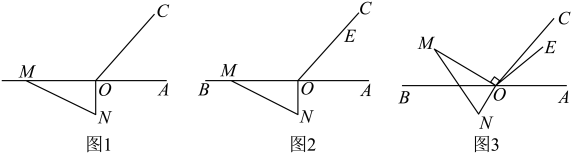
参考小炎同学思考问题的方法，解决下列问题：

（1）写出小炎的推理过程；

（2）如图3，四边形ABCD中， $\text{[math]}$ ， $\text{[math]}$ ，点E、F分别在边 $\text{[math]}$ 上， $\text{[math]}$ ，若 $\text{[math]}$ 、 $\text{[math]}$ 都不是直角，则当 $\text{[math]}$ 与 $\text{[math]}$ 满足于关系时，仍有 $\text{[math]}$ ；

（3）如图4，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点D、E均在边BC上，且 $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ，求DE的长.

查看解析收藏纠错

+选题
11. 请阅读下列材料：已知：如图（1）在 $\text{[math]}$ 中， $\text{[math]}$ ，点D、E分别为线段 $\text{[math]}$ 上两动点，若 $\text{[math]}$ .探究线段 $\text{[math]}$ 三条线段之间的数量关系.小明的思路是：把 $\text{[math]}$ 绕点A顺时针旋转 $\text{[math]}$ ，得到 $\text{[math]}$ ，连接 $\text{[math]}$ ，使问题得到解决.请你参考小明的思路探究并解决下列问题：

（1）猜想 $\text{[math]}$ 三条线段之间存在的数量关系式，直接写出你的猜想；

（2）当动点E在线段 $\text{[math]}$ 上，动点D运动在线段 $\text{[math]}$ 延长线上时，如图（2），其它条件不变，（1）中探究的结论是否发生改变？请说明你的猜想并给予证明；

（3）已知：如图（3），等边三角形 $\text{[math]}$ 中，点D、E在边 $\text{[math]}$ 上，且 $\text{[math]}$ ，请你找出一个条件，使线段 $\text{[math]}$ 能构成一个等腰三角形，并求出此时等腰三角形顶角的度数.

查看解析收藏纠错

+选题
12. 如图，将两个完全相同的三角形纸片 $\text{[math]}$ 和 $\text{[math]}$ 重合放置，其中 $\text{[math]}$ ， $\text{[math]}$ ．

（1）操作发现
如图②，固定 $\text{[math]}$ ，使 $\text{[math]}$ 绕点C旋转，当点D恰好落在 $\text{[math]}$ 边上时，
①求线段 $\text{[math]}$ 与 $\text{[math]}$ 的位置关系；
②设 $\text{[math]}$ 的面积为 $\text{[math]}$ ， $\text{[math]}$ 的面积为 $\text{[math]}$ ，求 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系．

（2）猜想论证
当 $\text{[math]}$ 绕点C旋转到如图③所示的位置时，小明猜想（1）中 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系仍然成立，并尝试分别作出了 $\text{[math]}$ 和 $\text{[math]}$ 中 $\text{[math]}$ 、 $\text{[math]}$ 边上的高，请你证明小明的猜想．

查看解析收藏纠错

+选题
13. 综合与实践
问题情境：
将两个完全相同的等腰Rt△ABC和等腰Rt△CDE按图1方式放置，∠ACB=∠DCE=90°，将Rt△CDE绕点C顺时针旋转，连接AE，BD，AE与BD相交于点G．
猜想证明：

（1）在图1中，请判断AE与BD的数量关系与位置关系，并说明理由；

（2）当旋转到CE//AB时，如图2，证明：AE平分∠BAC；

（3）若旋转到如图3所示的位置时，连接BE、此时△BCE恰好是等边三角形，AE与BC相交于点F，请你直接写出 $\text{[math]}$ 的值．

查看解析收藏纠错

+选题
14. 含有 $\text{[math]}$ 的直角三角板 $\text{[math]}$ 和含有 $\text{[math]}$ 的直角三角板 $\text{[math]}$ 按如图1放置， $\text{[math]}$ 和 $\text{[math]}$ 重合.

【操作一】三角板 $\text{[math]}$ 保持不变，将三角板 $\text{[math]}$ 绕着点 $\text{[math]}$ 以每秒 $\text{[math]}$ 的速度按逆时针方向旋转.当它完成旋转一周时停止，设旋转的时间为t秒.

（1）当 $\text{[math]}$ 时， $\text{[math]}$ 度.

（2）求t为何值时， $\text{[math]}$ .
【操作二】如图2，在三角板 $\text{[math]}$ 绕着点B以每秒 $\text{[math]}$ 的速度按逆时针方向旋转的同时，三角板 $\text{[math]}$ 也绕着点B以每秒 $\text{[math]}$ 的速度按逆时针方向旋转，设旋转时间为t秒（ $\text{[math]}$ ）.

（3）求t为何值时， $\text{[math]}$ 与 $\text{[math]}$ 重合.

（4）试探索：在两个三角板旋转的过程中，是否存在某个时刻，使得 $\text{[math]}$ 与 $\text{[math]}$ 中其中一个角是另一个角的两倍？若存在，请求出所有满足题意的t的值；若不存在，请说明理由.

查看解析收藏纠错

+选题
15. 通过类比联想、引申拓展研究典型题目，可达到解一题知一类的目的.下面是一个案例，请补充完整.

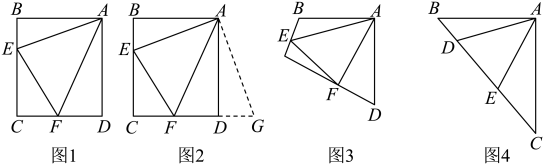
原题：如图1，点E、F分别在正方形ABCD的边BC、CD上，∠EAF=45°，连接EF，则EF=BE+DF，试说明理由.

（1）思路梳理
∵AB=CD，

∴把△ABE绕点A逆时针旋转90°至△ADG，可使AB与AD重合.

∵∠ADC=∠B=90°，

∴∠FDG=180°，点F、D、G共线.

根据，易证△AFG≌ ，得EF=BE+DF.

（2）类比引申
如图2，四边形ABCD中，AB=AD，∠BAD=90°，点E、F分别在边BC、CD上，∠EAF=45°.若∠B、∠D都不是直角，则当∠B与∠D满足等量关系时，仍有EF=BE+DF.

（3）联想拓展
如图3，在△ABC中，∠BAC=90°，AB=AC，点D、E均在边BC上，且∠DAE=45°.猜想BD、DE、EC应满足的等量关系，并写出推理过程.

查看解析收藏纠错

+选题
16. 某校一数学兴趣小组在一次合作探究活动中，将两块大小不同的等腰直角三角形 $\text{[math]}$ 和等腰直角三角形 $\text{[math]}$ ，按如图1的方式摆放， $\text{[math]}$ ，随后保持 $\text{[math]}$ 不动，将 $\text{[math]}$ 绕点C按逆时针方向旋转 $\text{[math]}$ （ $\text{[math]}$ ），连接 $\text{[math]}$ ， $\text{[math]}$ ，延长 $\text{[math]}$ 交 $\text{[math]}$ 于点F，连接 $\text{[math]}$ .该数学兴趣小组进行如下探究，请你帮忙解答：

【初步探究】

（1）如图2，当 $\text{[math]}$ 时，则 $\text{[math]}$ ；

（2）如图3，当点E，F重合时，请直接写出 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 之间的数量关系：；

（3）如图4，当点E，F不重合时，（2）中的结论是否仍然成立？若成立，请给出推理过程；若不成立，请说明理由.

（4）如图5，在 $\text{[math]}$ 与 $\text{[math]}$ 中， $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ （m为常数）.保持 $\text{[math]}$ 不动，将 $\text{[math]}$ 绕点C按逆时针方向旋转 $\text{[math]}$ （ $\text{[math]}$ ），连接 $\text{[math]}$ ， $\text{[math]}$ ，延长 $\text{[math]}$ 交 $\text{[math]}$ 于点F，连接 $\text{[math]}$ ，如图6.试探究 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 之间的数量关系，并说明理由.

查看解析收藏纠错

+选题
17. 如图

（1）（问题发现）
如图1，在Rt△ABC中，AB＝AC，D为BC边上一点（不与点B、C重合）将线段AD绕点A顺时针旋转90°得到AE，连结EC，则线段BD与CE的数量关系是，位置关系是；

（2）（探究证明）
如图2，在Rt△ABC和Rt△ADE中，AB＝AC，AD＝AE，将△ADE绕点A旋转，当点C，D，E在同一直线时，BD与CE具有怎样的位置关系，并说明理由；

（3）（拓展延伸）
如图3，在Rt△BCD中，∠BCD＝90°，BC＝2CD＝4，将△ACD绕顺时针旋转，点C对应点E，设旋转角∠CAE为α（0°＜α＜360°），当点C，D，E在同一直线时，画出图形，并求出线段BE的长度．

查看解析收藏纠错

+选题

2023年中考数学探究性试题复习18 旋转

一、综合题

相关试卷 收起∨

相关试卷收起∨