2023年中考数学探究性试题复习4 乘法公式

修改时间：2023-05-22 浏览次数：70 类型：三轮冲刺编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、单选题

1. 如图，在长方形 $\text{[math]}$ 中， $\text{[math]}$ ，其内部有边长为a的正方形 $\text{[math]}$ 与边长为b的正方形 $\text{[math]}$ ，两个正方形的重合部分也为正方形，且面积为5，若 $\text{[math]}$ ，则正方形 $\text{[math]}$ 与正方形 $\text{[math]}$ 的面积之和为（）

A . 29 B . 25 C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
2. 如图（1），从边长为a的大正方形的四个角中挖去四个边长为b的小正方形后，将剩余的部分剪拼成一个长方形，如图（2），通过计算阴影部分的面积可以得到（）

A . （a-2b）²＝a²-4ab+b² B . （a+2b）²＝a²+4ab+b² C . （a-2b）（a+2b）＝a²-4b² D . （a+b）²＝a²+2ab+b²

查看解析收藏纠错

+选题
3. 如图，边长为 $\text{[math]}$ 的长方形周长为12，面积为5，则 $\text{[math]}$ 的值为（）

A . 60 B . 120 C . 130 D . 240

查看解析收藏纠错

+选题
4. 如图4张长为a、宽为b（a＞b）的长方形纸片，按如图的方式拼成一个边长为（a+b）的正方形，图中空白部分的面积为S₁ ，阴影部分的面积为S₂ ．若S₁＝2S₂ ，则a：b=（）

A . 3：2 B . 5：2 C . 2：1 D . 3：1

查看解析收藏纠错

+选题
5. 如下图（1），边长为a的大正方形中一个边长为b的小正方形，小明将图（1）的阴影部分拼成了一个矩形，如图（2）．这一过程可以验证（）

A . a²+b²-2ab=(a-b)² B . a²+b²+2ab=(a+b)² C . 2a²-3ab+b²=(2a-b)(a-b) D . a²-b²=(a+b) (a-b)

查看解析收藏纠错

+选题
6. 如图中能够用图中已有图形的面积说明的等式是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
7. 如图，是利用割补法求图形面积的示意图，下列公式中与之相对应的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
8. 根据图形（图1，图2）的面积关系，下列说法正确的是（）

A . 图1能说明勾股定理，图2能说明完全平方公式 B . 图1能说明平方差公式，图2能说明勾股定理 C . 图1能说明完全平方公式，图2能说明平方差公式 D . 图1能说明完全平方公式，图2能说明勾股定理

查看解析收藏纠错

+选题

二、填空题

9. 乘法公式的探究及应用.

小题1：如图1，可以求出阴影部分的面积是 (写成两数平方差的形式)；

小题2：如图2，若将阴影部分裁剪下来，重新拼成一个矩形，它的宽是，长是，面积是 (写成多项式乘法的形式).

小题3：比较图 1，图2的阴影部分面积，可以得到乘法公式 (用式子表达).

查看解析收藏纠错

+选题
10. 我国古代数学家赵爽的“勾股圆方图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形（如图所示）.如果大正方形的面积是13，小正方形的面积是1，直角三角形的两直角边长分别为a、b ，那么 $\text{[math]}$ 的值是.

查看解析收藏纠错

+选题
11. 如图1，在边长为a的大正方形中，剪去一个边长为3的小正方形，将余下的部分按图中的虚线剪开后，拼成如图2所示的长方形．根据两个图形阴影部分面积相等的关系，可以列出的等式为．

查看解析收藏纠错

+选题
12. 在数学学习中，我们常把数或表示数的字母与图形结合起来，著名数学家华罗庚曾用诗词表达了“数形结合”的思想，其中谈到“数缺形时少直观，形少数时难入微”.如图是由四个长为a，宽为b的长方形拼摆而成的正方形，其中a＞b＞0，若ab=3，a+b=4，则a-b的值为.

查看解析收藏纠错

+选题
13. $\text{[math]}$ ， $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ，请借助下图直观分析，通过计算求得 $\text{[math]}$ 的值为．

查看解析收藏纠错

+选题

三、综合题

14. 从边长为 $\text{[math]}$ 的正方形减掉一个边长为 $\text{[math]}$ 的正方形（如图1），然后将剩余部分拼成一个长方形（如图2）．

（1）上述过程所揭示的乘法公式是．

（2）若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的值．

（3）计算： $\text{[math]}$ ．

查看解析收藏纠错

+选题
15. 如图1，有 $\text{[math]}$ 型、 $\text{[math]}$ 型、 $\text{[math]}$ 型三种不同形状的纸板， $\text{[math]}$ 型是边长为 $\text{[math]}$ 的正方形， $\text{[math]}$ 型是边长为 $\text{[math]}$ 的正方形， $\text{[math]}$ 型是长为 $\text{[math]}$ ，宽为 $\text{[math]}$ 的长方形. 现用 $\text{[math]}$ 型纸板一张， $\text{[math]}$ 型纸板一张， $\text{[math]}$ 型纸板两张拼成如图2的大正方形．

（1）观察图2，请你用两种方法表示出图2的总面积.
方法1：；
方法2：；
请利用图2的面积表示方法，写出一个关于 $\text{[math]}$ ， $\text{[math]}$ 的等式：．.

（2）已知图2的总面积为64，一张 $\text{[math]}$ 型纸板和一张 $\text{[math]}$ 型纸板的面积之和为40，求 $\text{[math]}$ 的值.

（3）用一张 $\text{[math]}$ 型纸板和一张 $\text{[math]}$ 型纸板，拼成图3所示的图形，若 $\text{[math]}$ ， $\text{[math]}$ 求图3阴影部分的面积．

查看解析收藏纠错

+选题
16. 通过构造一个图形，利用两种方法计算该图形的面积，从而得到一个等式，这种方法习惯称为“算两次”，在数学学习中有着广泛的应用．公元三世纪，三国时代的赵爽创制了“勾股圆方图”，验证了著名的勾股定理．

（1）如图1，边长为 $\text{[math]}$ 的大正方形 $\text{[math]}$ 中有一个边长为 $\text{[math]}$ 的小正方形 $\text{[math]}$ ．请你用两种不同方法求阴影部分的面积；

（2）如图2，现有若干张 $\text{[math]}$ 型、 $\text{[math]}$ 型、 $\text{[math]}$ 型三种不同形状的纸片，请你利用纸片拼出一个几何图形直观地解释 $\text{[math]}$ ；

（3）在（1）的条件下，若 $\text{[math]}$ ， $\text{[math]}$ ，一动点 $\text{[math]}$ 以每秒 $\text{[math]}$ 的速度从点 $\text{[math]}$ 出发，沿着 $\text{[math]}$ 方向运动．
①当点 $\text{[math]}$ 在 $\text{[math]}$ 上运动时，请表示出 $\text{[math]}$ 的面积 $\text{[math]}$ 与 $\text{[math]}$ 的关系式： ▲ ；
②是否存在 $\text{[math]}$ 使得 $\text{[math]}$ 的面积为 $\text{[math]}$ ，若存在，求出 $\text{[math]}$ 的值；若不存在，请说明理由．

查看解析收藏纠错

+选题
17. 现有长与宽分别为 $\text{[math]}$ 、 $\text{[math]}$ 的小长方形若干个，用两个这样的小长方形拼成如图1的图形，用四个相同的小长方形拼成图2的图形，请认真观察图形，解答下列问题：

（1）根据图中条件，请写出图1和图2所验证的关于 $\text{[math]}$ 、 $\text{[math]}$ 的关系式：（用含 $\text{[math]}$ 、 $\text{[math]}$ 的代数式表示出来）；
图1表示：；
图2表示：；

（2）根据上面的解题思路与方法，解决下列问题：
①若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的值；
②请直接写出下列问题故答案为：
若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ ▲ ；
若 $\text{[math]}$ ，则 $\text{[math]}$ ▲ ．

（3）如图，长方形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，长方形 $\text{[math]}$ 的面积是200，四边形 $\text{[math]}$ 和 $\text{[math]}$ 都是正方形，四边形 $\text{[math]}$ 是长方形．延长 $\text{[math]}$ 至 $\text{[math]}$ ，使 $\text{[math]}$ ，延长 $\text{[math]}$ 至 $\text{[math]}$ ，使 $\text{[math]}$ ，过点 $\text{[math]}$ 、 $\text{[math]}$ 作 $\text{[math]}$ 、 $\text{[math]}$ 的垂线，两垂线相交于点 $\text{[math]}$ ，求四边形 $\text{[math]}$ 的面积．（结果必须是一个具体的数值）

查看解析收藏纠错

+选题
18. 如图1所示是一个长为 $\text{[math]}$ 、宽为 $\text{[math]}$ 的长方形，沿图中虚线用剪刀均分成四块小长方形，然后按图2的形状拼成一个正方形．

（1）观察图2，请你直接写出下列三个代数式 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 之间的等量关系为；

（2）运用你所得到的公式解答下列问题：
①若m，n为实数，且 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的值．
②如图3， $\text{[math]}$ ， $\text{[math]}$ 分别表示边长为p，q的正方形的面积，且A，B，C三点在一条直线上，若 $\text{[math]}$ ， $\text{[math]}$ ，求图中阴影部分的面积．

查看解析收藏纠错

+选题
19. 如图(a)所示，边长为a的大正方形中有一个边长为b的小正方形，把图(a)中的阴影部分拼成一个如图(b)所示的长方形．

（1）通过观察比较图(b)与图(a)中的阴影部分面积，可以得到乘法公式(用含a，b的等式表示)

（2） (应用)请应用这个公式完成下列各题：
①若a+2b=3，2b-a=2，则a²-4b²的值为
②若4m²=12+n，2m+n=4，则2m-n的值为

（3） (拓展)计算：100² -992+98²-97²+……+4²-3²+2²-1² ．

查看解析收藏纠错

+选题
20. 把几个图形拼成一个新的图形，再通过两种不同的方法计算同一个图形的面积，可以得到一个等式.例如：由图1，可得等式： $\text{[math]}$ .

（1）观察图2，请你写出 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 之间的一个恒等式： $\text{[math]}$ ；

（2）根据（1）的结论，若 $\text{[math]}$ ， $\text{[math]}$ ，求下列各式的值：
① $\text{[math]}$ ；② $\text{[math]}$ .

查看解析收藏纠错

+选题
21. 发现：一个两位数的平方与其个位数字的平方的差，一定是 $\text{[math]}$ 的倍数．如： $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 的 $\text{[math]}$ 倍； $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 的 $\text{[math]}$ 倍．

（1）请你仿照上面的例子，再举出一个例子： $\text{[math]}$ ；

（2）十位数字为1，个位数字为 $\text{[math]}$ 的两位数可表示为，若该两位数的平方与 $\text{[math]}$ 的平方的差是 $\text{[math]}$ 的 $\text{[math]}$ 倍，则 $\text{[math]}$ ；

（3）设一个两位数的十位数字为 $\text{[math]}$ ，个位数字为 $\text{[math]}$ （ $\text{[math]}$ ， $\text{[math]}$ ，且 $\text{[math]}$ ， $\text{[math]}$ 为正整数），请用含 $\text{[math]}$ ， $\text{[math]}$ 的式子论证“发现”的结论是否符合题意．

查看解析收藏纠错

+选题
22. 灵活运用完全平方公式 $\text{[math]}$ 可以解决许多数学问题．
例如：已知 $\text{[math]}$ ，求 $\text{[math]}$ 的值．
解： $\text{[math]}$ ， ∴ $\text{[math]}$ ，
$\text{[math]}$ ．
请根据以上材料，解答下列问题．

（1）若 $\text{[math]}$ 与 $\text{[math]}$ 互为相反数，求 $\text{[math]}$ 的值．

（2）如图，矩形的长为a，宽为b，周长为14，面积为8，求 $\text{[math]}$ 的值．

查看解析收藏纠错

+选题
23. 如图

（1）【观察】如图1是一个长为 $\text{[math]}$ 、宽为 $\text{[math]}$ 的长方形，沿图中虚线用剪刀平均分成四块小长方形，然后用四块小长方形拼成一个“回形”正方形（如图2）.请你写出 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 之间的等量关系：；

（2）【应用】若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ ；

（3）【拓展】如图3，正方形 $\text{[math]}$ 的边长为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，长方形 $\text{[math]}$ 的面积是300，四边形 $\text{[math]}$ 和四边形 $\text{[math]}$ 都是正方形，四边形 $\text{[math]}$ 是长方形，求图中阴影部分的面积.

查看解析收藏纠错

+选题
24. 利用平面图形中面积相等的等量关系可以得到某些数学公式.例如：根据图①，我们可以得到两数和的平方公式：（a＋b）²＝a²＋2ab＋b².

（1）根据图②，可以得到的数学公式是；

（2）根据图③，请写出（a＋b）、（a－b）、ab的等量关系是.

（3）根据图④，请写出一个等式：；

（4）小明同学使用图⑤中x张边长为a的正方形，y张边长为b的正方形，z张宽、长分别为a、b的长方形纸片，恰好拼成一个面积为（3a＋b）（a＋3b）的长方形，则可得x＋y＋z的值为；

（5）类似地，利用立体图形体积的等量关系也可以得到某些数学公式.现请你根据图⑥，写出一个等式：.

查看解析收藏纠错

+选题
25. 数学中，常对同一个量用两种不同的方法计算，从而建立相等关系，我们把这一思想称为“算两次”．

（1） [探究一]

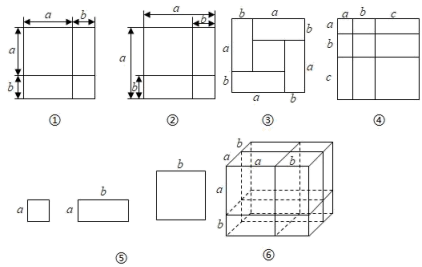
方法1：如图1，在边长为a的正方形纸片上剪去一个边长为b(b<a)的正方形，你能表示图中阴影部分的面积吗？阴影部分的面积是.

方法2：如图2．也可以把阴影部分沿着虚线AB剪开，分成两个梯形，计算阴影部分的面积是.

用两种不同的方法计算同一个阴影部分的面积，可以得到等式.

（2） [探究二]
如图3，一条直线上有n个点，请你数一数共有多少条线段呢？
方法1：一路往右数，不回头数．
以A₁为端点的线段有A₁A₂、A₁A₃、A₁A₄、A₁A₅、……A₁A_n ，共有(n-1)条；
以A₂为端点的线段有A₂A₃、A₂A₄、A₂A₅、……A₂A_n ，共有(n-2)条；
以A₃为端点的线段有A₃A₄、A₃A₅、……A₃A_n ．共有(n-3)条；
以A_n-1为端点的线段有A_n-1A_n ，共有1条；图中线段的总条数可用加法算式表示为.
方法2：每一个点都能和除它以外的(n-1)个点形成线段，共有n个点，共可形成n(n-1)条线段，但所有线段都数了两遍，所以线段的总条数是.
用两种不同的方法数线段，可以得到等式.

（3） [类比探究]如图，AC⊥BC，AC=3cm，BC=4cm，AB=5cm，点D为AB边的动点，求线段CD的最小值．

（4） [探究应用]计算：99²-98²+97²-96²+95²-94²+……+3²-2²+1² ．

查看解析收藏纠错

+选题

2023年中考数学探究性试题复习4 乘法公式

一、单选题

二、填空题

三、综合题

相关试卷 收起∨

相关试卷收起∨