修改时间:2025-01-06 浏览次数:5 类型:复习试卷
主题:制作一个无盖长方形盒子.
步骤1:按照如图所示的方式,将正方形纸片的四个角剪掉四个大小相同的小正方形.
步骤2:沿虚线折起来,就可以做成一个无盖的长方体盒子.
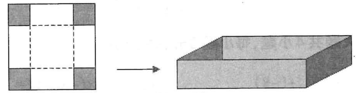
如果原正方形纸片的边长为 , 剪去的正方形的边长为
, 则折成的无盖长方体盒子的高、底面积、容积分别为、、(请你用含a,b的代数式来表示).
剪去正方形的边长 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
容积 | 324 | 512 | m | n | 500 | 384 | 252 | 128 | 36 | 0 |
观察绘制的统计表,你发现,随着减去的小正方形的边长的增大,所折无盖长方体盒子的容积如何变化?并分析猜想当剪去图形的边长为多少时,所得的无盖长方体的容积最大,此时最大容积是多少?
操作一:根据图1方式制作一个无盖的长方体盒子,方法是:先在纸板四角剪去四个同样大小边长为b的小正方形,再沿虚线折合起来.并设该长方体的长、宽、高之和为
.

操作二:根据图2方式制作一个有盖的长方体纸盒.方法:先在纸板四角剪去两个同样大小边长为bcm的小正方形和两个同样大小的小长方形,再沿虚线折合起来.并设该长方体的长、宽、高之和为 .

主题:制作一个无盖长方形盒子.
步骤1:按照如图所示的方式,将正方形纸片的四个角剪掉四个大小相同的小正方形.
步骤2:沿虚线折起来,就可以做成一个无盖的长方体盒子.
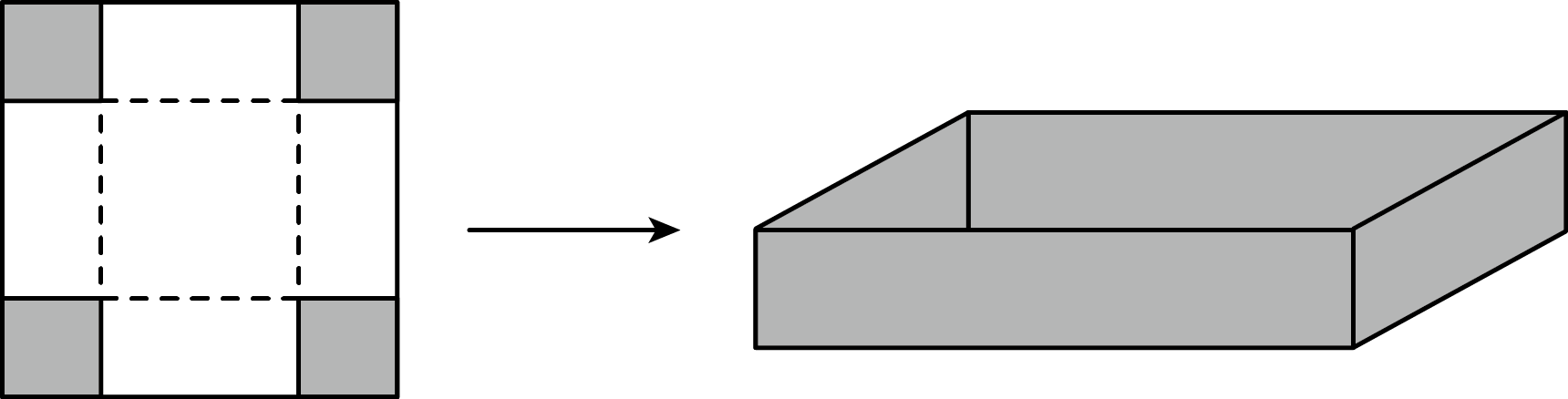
如果原正方形纸片的边长为a,剪去的正方形的边长为b,则折成的无盖长方体盒子的高、底面积、容积分别为、、(请你用含a,b的代数式来表示).
如果 , 剪去的小正方形的边长按整数值依次变化,即分别取
,
,
,
,
,
,
,
,
,
时,折成的无盖长方体的容积分别是下表数据,请求出m和n分别是多少?
剪去正方形的边长/ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
容积/ | 324 | 512 | m | n | 500 | 384 | 252 | 128 | 36 | 0 |
观察绘制的统计表,你发现,随着减去的小正方形的边长的增大,所折无盖长方体盒子的容积如何变化?并分析猜想当剪去图形的边长为多少时,所得的无盖长方体的容积最大,此时最大容积是多少?
如图是某月的日历.
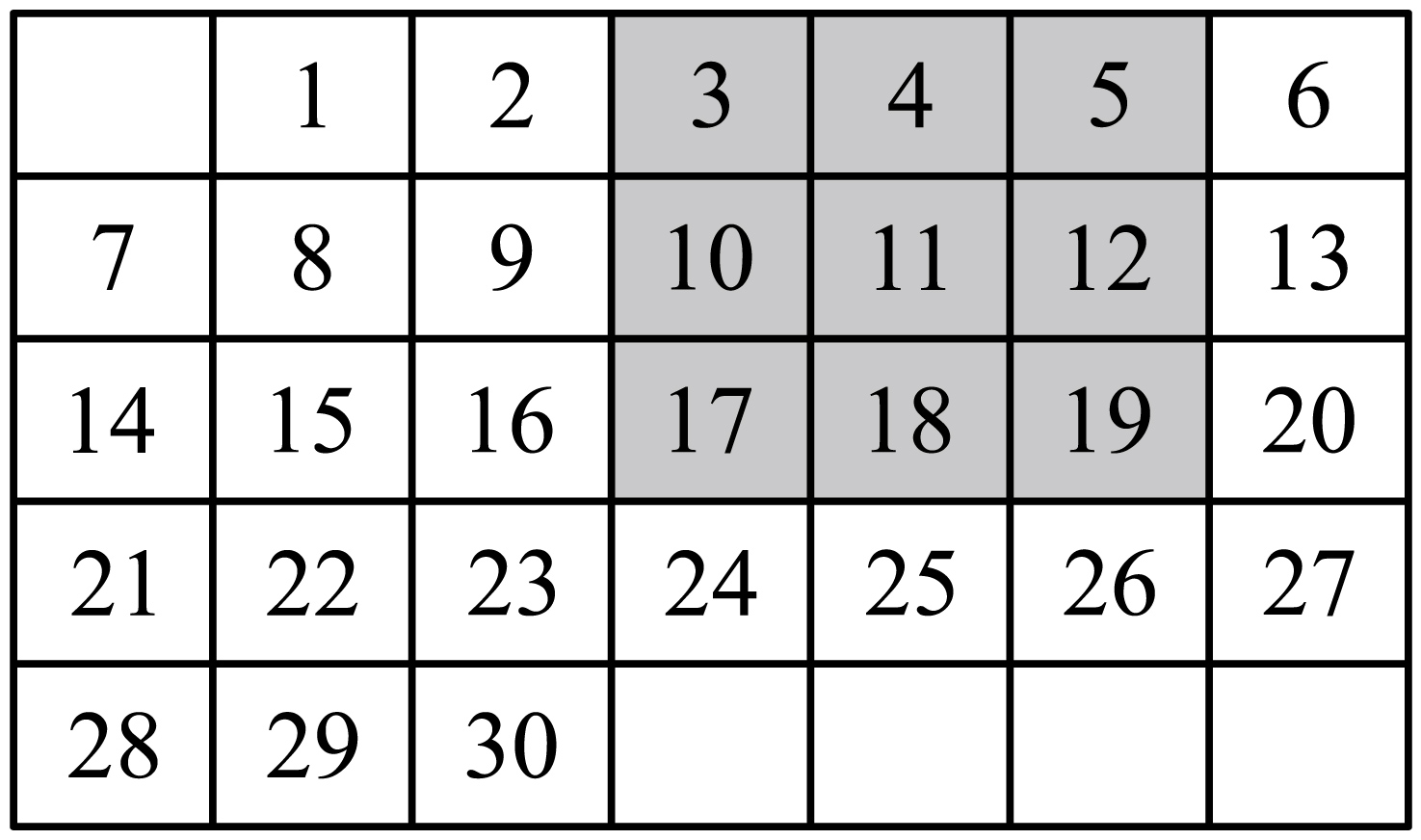
①带阴影的方框中的9个数之和与方框正中的数有什么关系?
②不改变方框的大小如果将带阴影的方程移至其他几个位置试一试,上述关系还成立吗?如成立,请说明为什么成立.
小明是个爱动脑筋的同学,在发现教材中的用方框在月历中移动的规律后,突发奇想,将连续的偶数2,4,6,8,…,排成如图形式,并用一个十字形框架框住其中的五个数,请你仔细观察十字形框架中的数字的规律,并回答下列问题:
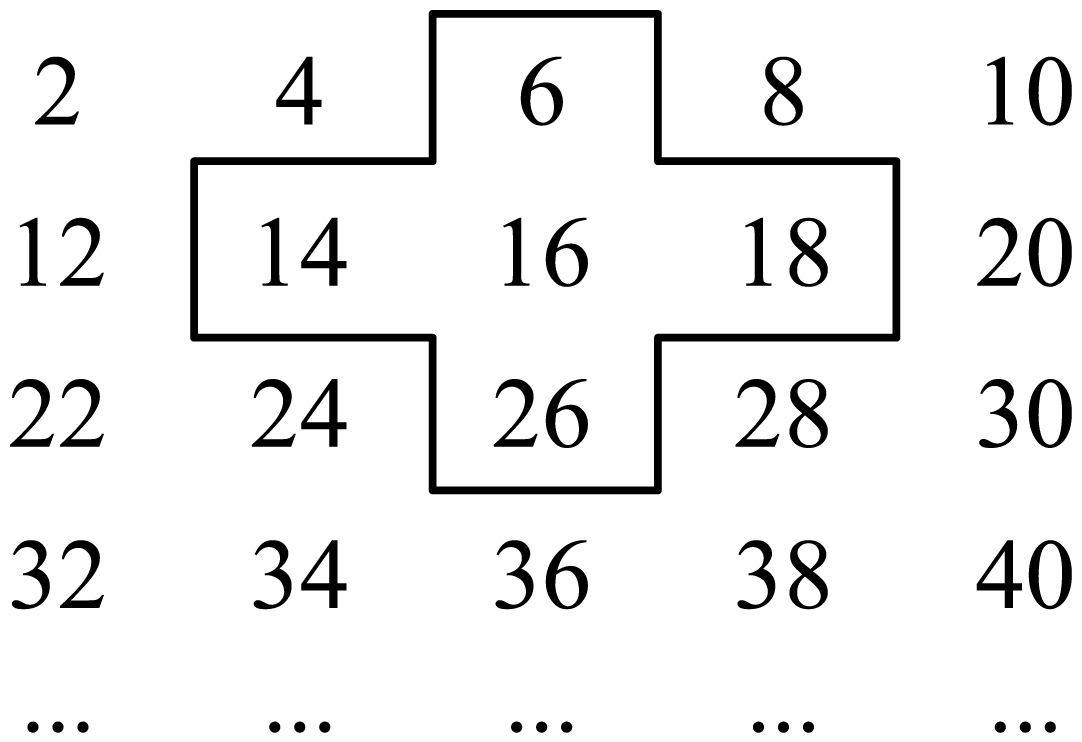
①十字框中的五个数的和与中间的数16有什么关系?
②设中间的数为x,用代数式表示十字框中的五个数的和;
③若将十字框上下左右移动,可框住另外的五个数,其它五个数的和能等于2010吗?如能,写出这五个数,如不能,说明理由.
整体思想是一种重要的数学思想方法,其思维方式是根据问题的结构特征,把一组数,一个代数式或几个图形视为一个整体,去观察,分析,解决问题的一种方法.这样做,不仅简化解题过程,提高思维能力,还往往可以解决按常方法解决不了的一些问题.
如:代数式的化简问题.若把
看成一个整体,
则: .
这就是数学解题中的“整体思想”.
请运用上面的“整体思想”解决下列问题:

商品条形码在生活中随处可见,它是商品的身份证.条形码是由13位数字(每个数字都是由大于等于0且小于等于9的整数)组成,前12位数字分别表示“国家代码、出口商识别码和商品代码”相关信息,如图①693是代表中国,49170代表出口商识别码,0940代表商品代码,第13位数字2为“校验码”.其中,校验码是用来校验商品条形码中前12位数字代码的正确性,它的编制是按照特定算法得来的,具体算法如下(以图①为例):
步骤 | 举例说明 | |||||||||||||
步骤1:自左向右编号: | 某商品的条形码:693489170940X(X为校验码) | |||||||||||||
位置序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | |
代码 | 6 | 9 | 3 | 4 | 9 | 1 | 7 | 0 | 0 | 9 | 4 | 0 | X | |
步骤2:求前12位数字中偶数位上的数字之和s; |
| |||||||||||||
步骤3:求前12为数字钟奇数位上的数字之和t; |
| |||||||||||||
步骤4:计算 |
| |||||||||||||
步骤5:取大于或等于m且为10的最小整数倍数n; |
| |||||||||||||
步骤6:计算n与m的差就是校验码X. |
| |||||||||||||
【知识运用】请回答下列问题:
步骤1:自左向右编号,共13位;
步骤2:求前12位数字中偶数位上的数字之和;
步骤3:求前12位数字中奇数位上的数字之和;
步骤4:计算与t的和
;
步骤5:取大于或等于m且为10的最小整数倍数;
步骤6:计算n与m的差就是校验码.

如图1,用一根质地均匀的的木杆和一些等重量的小物体做下列实验,并记录每一次支点到木杆左右两边挂重物的距离:
①在木杆中间处栓绳作为支点,将木杆吊起来并使左右平衡;
②在木杆两端各悬挂一重物,看左右是否保持平衡;
③在木杆左端小物体下加挂一重物,然后把这两个重物一起向右移动,直至左右平衡;
④在木杆左边继续加挂重物,并重复以上操作和记录如下:


图1 图2
木杆左边挂 重物个数 | 支点到木杆左边挂 重物的距离 | 木杆右端挂 重物个数 | 支点到木杆右端挂 重物的距离 |
1 | 1 | ||
2 | 1 | ||
3 | 1 | ||
…… | …… | 1 | |
…… | 1 |
试题篮