2022-2023学年浙教版数学九上期中复习专题1 二次函数的图象与性质

修改时间：2022-10-17 浏览次数：146 类型：复习试卷编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、单选题每题3分，共30分）

1. 下列函数中，是二次函数的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
2. 如图，若抛物线 $\text{[math]}$ 经过原点，则抛物线的解析式为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$ 或 $\text{[math]}$

查看解析收藏纠错

+选题
3. 抛物线 $\text{[math]}$ 的对称轴是（）

A . 直线 $\text{[math]}$ B . 直线 $\text{[math]}$ C . 直线 $\text{[math]}$ D . 直线 $\text{[math]}$

查看解析收藏纠错

+选题
4. 在同一直角坐标系中，函数 $\text{[math]}$ 和函数 $\text{[math]}$ (a是常数，且a≠0)的图象可能是（）

A . B . C . D .

查看解析收藏纠错

+选题
5. 若在同一平面直角坐标系中，作y＝3x² ， y＝x²﹣2，y＝﹣2x²+1的图象，则它们（）

A . 开口方向相同 B . 互相可以通过平移得到 C . 都经过原点 D . 都关于y轴对称

查看解析收藏纠错

+选题
6. 抛物线 $\text{[math]}$ 的顶点坐标是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
7. 已知二次函数 $\text{[math]}$ ，当 $\text{[math]}$ 时，对应的函数值y不可能是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 4 D . 5

查看解析收藏纠错

+选题
8. 已知二次函数y＝x²﹣2x+3，关于该函数在﹣2≤x≤2的取值范围内，下列说法正确的是（）

A . 有最大值11，有最小值3 B . 有最大值11，有最小值2 C . 有最大值3，有最小值2 D . 有最大值3，有最小值1

查看解析收藏纠错

+选题
9. 二次函数 $\text{[math]}$ 的部分图象如图所示，当 $\text{[math]}$ 时，函数值 $\text{[math]}$ 的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
10. 如图所示，已知二次函数 $\text{[math]}$ 的图象与 $\text{[math]}$ 轴交于 $\text{[math]}$ 、 $\text{[math]}$ 两点，与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ， $\text{[math]}$ ．对称轴为直线 $\text{[math]}$ ，则下列结论：① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ ；④ $\text{[math]}$ 是关于 $\text{[math]}$ 的一元二次方程 $\text{[math]}$ 的一个根，其中正确的有（）

A . 4个 B . 3个 C . 2个 D . 1个

查看解析收藏纠错

+选题

二、填空题（每题4分，共24分）

11. 一个矩形的周长为16cm，设一边长为xcm，面积为y $\text{[math]}$ ，那么y与x的关系式是

查看解析收藏纠错

+选题
12. 将抛物线 $\text{[math]}$ 先向右平移2个单位，再向下平移3个单位得到的抛物线所对应的函数表达式为。

查看解析收藏纠错

+选题
13. 将二次函数y=x²-2x+3化为y=（x-h）²+k的形式，则h=，k=．

查看解析收藏纠错

+选题
14. 若点A（x₁ ， m）和点B（x₂ ， m）（x₁≠x₂）都在二次函数y＝ $\text{[math]}$ x²﹣1的图象上，则当x＝x₁+x₂时，函数y的值是．

查看解析收藏纠错

+选题
15. 已知二次函数 $\text{[math]}$ ，当 $\text{[math]}$ 时，y随x的增大而增大，则m的取值范围是．

查看解析收藏纠错

+选题
16. 若点M(﹣1，y₁)，N(1，y₂)，P( $\text{[math]}$ ， y₃)都在抛物线y＝﹣ax²+4ax+a²+1（a＞0）上，则y₁ ， y₂ ， y₃大小关系是（用＜号连接）．

查看解析收藏纠错

+选题

三、解答题（共8题，共66分）

17. 已知二次函数 $\text{[math]}$ 的图象经过点 $\text{[math]}$ .

（1）求这个二次函数的表达式；

（2）画出这个函数的图象，并利用图象解决下列问题：
①直接写出方程 $\text{[math]}$ 的解；

②当x满足什么条件时， $\text{[math]}$ .

查看解析收藏纠错

+选题
18. 一个二次函数的图象经过 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 三点．求：这个二次函数的解析式．

查看解析收藏纠错

+选题
19. 已知点（0，3）在二次函数 $\text{[math]}$ 的图象上，且当 $\text{[math]}$ 时，函数 $\text{[math]}$ 有最小值2，这个二次函数的表达式。

查看解析收藏纠错

+选题
20. 已知二次函数y＝mx²﹣2mx+3，其中m≠0.

（1）若二次函数的图象经过（1，4），求二次函数表达式；

（2）若该二次函数图象开口向上，当﹣1≤x≤2时，二次函数图象的最高点为M，最低点为N，点M的纵坐标为6，求点M和点N的坐标；

（3）在二次函数图象上任取两点（x₁ ， y₁），（x₂ ， y₂），当a≤x₁＜x₂≤a+2时，总有y₁＞y₂ ，求a的取值范围.

查看解析收藏纠错

+选题

21. 已知一个二次函数图象上部分点的横坐标 $\text{[math]}$ 与纵坐标 $\text{[math]}$ 的对应值如下所示：

$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	0	1	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$	0	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	0	$\text{[math]}$

（1）求这个二次函数的表达式，并画出图象；

（2）当 $\text{[math]}$ 时，直接写出 $\text{[math]}$ 的取值范围；

（3）若该图象与 $\text{[math]}$ 轴的两交点分别记为 $\text{[math]}$ ，且 $\text{[math]}$ 在 $\text{[math]}$ 的左侧，点 $\text{[math]}$ 在该二次函数图象上，求 $\text{[math]}$ 的面积.

查看解析收藏纠错

+选题

22. 如图，二次函数图象与x轴交于点A、B，与y轴交与点C，抛物线的顶点坐标是（2，9），且经过D（3，8）．

（1）求抛物线的函数关系式；

（2）求△ABC的面积；

（3）在抛物线的对称轴上是否存在一点M，使得BM＋DM最短？若存在，求出M的坐标．若不存在，请说明理由．

查看解析收藏纠错

+选题
23. 如图，已知抛物线 $\text{[math]}$ 与x轴交于点， $\text{[math]}$ ， $\text{[math]}$ ，与y轴交与点D．过点 $\text{[math]}$ 的直线AC与抛物线交与A，F两点．

（1）求抛物线的解析式；

（2）点P为直线AF下方抛物线上一动点，过点P作y轴的平行线交AC于点Q，过点Р作x轴的平行线交y轴于点E，求 $\text{[math]}$ 的最大值及相应点Р的坐标；

（3）在（2）的条件下，将抛物线 $\text{[math]}$ 先向右平移2个单位，再向下平移1个单位，得到新抛物线 $\text{[math]}$ ，点M为 $\text{[math]}$ 对称轴上一点，点N为 $\text{[math]}$ 上一点，若以点D，P，M，N为顶点的四边形为平行四边形，写出所有符合条件的点M的坐标，并任选其中一个点M的坐标写出求解过程．

查看解析收藏纠错

+选题
24. 《函数的图象与性质》拓展学习片段展示：

（1）（问题）
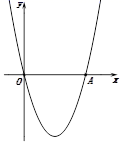
如图①，在平面直角坐标系中，抛物线y=a（x-2）²-4经过原点O，与x轴的另一个交点为A，则a= ，点A的坐标为 .

（2）（操作）
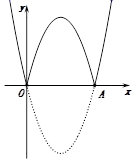
将图①中的抛物线在x轴下方的部分沿x轴翻折到x轴上方，如图②.直接写出翻折后的这部分抛物线对应的函数解析式：.

（3）（探究）
在图②中，翻折后的这部分图象与原抛物线剩余部分的图象组成了一个“W”形状的新图象，则新图象对应的函数y随x的增大而增大时，x的取值范围是.

（4）（应用）结合上面的操作与探究，继续思考：如图③，若抛物线y=（x-h）²-4与x轴交于A，B两点（A在B左），将抛物线在x轴下方的部分沿x轴翻折，同样，也得到了一个“W”形状的新图象.
求A、B两点的坐标；（用含h的式子表示）

（5）当1＜x＜2时，若新图象的函数值y随x的增大而增大，求h的取值范围.

查看解析收藏纠错

+选题

2022-2023学年浙教版数学九上期中复习专题1 二次函数的图象与性质

一、单选题每题3分，共30分）

二、填空题（每题4分，共24分）

三、解答题（共8题，共66分）

相关试卷 收起∨

相关试卷收起∨