湖北省荆州市2020年九年级调研考试数学试卷

1. 在下列四个实数 $\text{[math]}$ ，-0.5，0， $\text{[math]}$ 中，最小的是（）

A . $\text{[math]}$ B . - 0.5 C . 0 D . $\text{[math]}$

查看解析收藏纠错

+选题
2. 下列计算结果正确的是（）

A . a⁶÷a²＝a³ B . （ab）²＝a²b² C . a⁴·a²＝a⁸ D . （a⁴）²＝a⁶

查看解析收藏纠错

+选题
3. 下列立体图形中，俯视图与主视图不同的是（）

A . 正方体 B . 圆柱 C . 圆锥 D . 球

查看解析收藏纠错

+选题
4. 如图是婴儿车的平面示意图，其中AB∥CD，∠1=120°，∠3=40°，那么∠2的度数为（）

A . 80° B . 90° C . 100° D . 102°

查看解析收藏纠错

+选题
5. 防范新冠病毒感染要养成戴口罩、勤洗手、多通风、常消毒等卫生习惯，其中对物体表面进行消毒可以采用浓度为75％的酒精.现有一瓶浓度为95％的酒精500mL，需将其加入适量的水，使浓度稀释为75％.设加水量为xml，可列方程为（）

A . 75％x＝95％×500 B . 95％x＝75％×500 C . 75％（500＋x）＝95％×500 D . 95％（500＋x）＝75％×500

查看解析收藏纠错

+选题
6. 若单项式－3x²y^2m+n与2x^m+ny⁴是同类项，则m²＋2mn的算术平方根为（）

A . 0 B . 2 C . －2 D . ±2

查看解析收藏纠错

+选题
7. 定义（a，b，c）为方程 $\text{[math]}$ 的特征数.若特征数为（ $\text{[math]}$ ， $\text{[math]}$ ，1）的一元二次方程有两个实数根，则k的取值范围是（）

A . $\text{[math]}$ ＜ $\text{[math]}$ B . k ＞ $\text{[math]}$ C . k ＞ $\text{[math]}$ 且 $\text{[math]}$ D . k≥ $\text{[math]}$ 且 $\text{[math]}$

查看解析收藏纠错

+选题
8. 如图，将⊙O沿弦AB折叠，圆弧恰好经过圆心O，点P是优弧 $\text{[math]}$ 上一点，则∠APB的度数为（）

A . 45° B . 30° C . 75° D . 60°

查看解析收藏纠错

+选题
9. 二次函数y＝ax²＋bx＋c的图象如图所示，则一次函数y＝bx＋ac的图象不经过（）

A . 第一象限 B . 第二象限 C . 第三象限 D . 第四象限

查看解析收藏纠错

+选题
10. 如图，6个形状、大小完全相同的菱形组成网格，菱形的顶点称为格点. 已知菱形的一个角（∠O）为60°，A，B，C 都在格点上，则tan∠ABC的值是（）.

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题

11. 将3x²﹣27分解因式的结果是 .

查看解析收藏纠错

+选题
12. 若点（1，k）关于y轴的对称点为（－1，1），则y关于x的函数 $\text{[math]}$ 的取值范围是.

查看解析收藏纠错

+选题
13. 点P的坐标是（a，b），从-2，-1，0，1，2这五个数中任取一个数作为a的值，再从余下的四个数中任取一个数作为b的值，则点P（a，b）在平面直角坐标系中第二象限内的概率是.

查看解析收藏纠错

+选题
14. 如图，在Rt∆ABC中，∠C＝90°，以顶点B为圆心，适当长度为半径画弧，分别交AB，BC于点M，N，再分别以点M，N为圆心，大于 $\text{[math]}$ 的长为半径画弧，两弧交于点P，作射线BP交AC于点D.当∠A＝30°时，小敏正确求得 $\text{[math]}$ ： $\text{[math]}$ ＝1：2.写出两条小敏求解中用到的数学依据：.

查看解析收藏纠错

+选题
15. 如图，某办公大楼正前方有一根高度是15米的旗杆ED，从办公大楼顶端A测得旗杆顶端E的俯角α是45°，旗杆底端D到大楼前梯坎底边的距离DC是20米，梯坎坡长BC是12米，梯坎坡度i＝1： $\text{[math]}$ ，则大楼AB的高度为米.（精确到0.1米，参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）

查看解析收藏纠错

+选题
16. 定义新运算：对于任意实数a，b，都有a⊕b＝ab＋a＋b，其中等式右边是通常的加法、乘法运算，例如2⊕3＝2×3＋2＋3＝11.若y关于x的函数y＝（kx＋1）⊕（x－1）图象与x轴仅有一个公共点，则实数k的值为.

查看解析收藏纠错

+选题

17. 先化简，再求值： $\text{[math]}$ ，其中x是不等式组 $\text{[math]}$ 的整数解.

查看解析收藏纠错

+选题
18. 若实数m，n满足 $\text{[math]}$ ，请用配方法解关于x的一元二次方程 $\text{[math]}$ .

查看解析收藏纠错

+选题
19. 如图，在正方形ABCD中，E为边BC上一点（不与点B，C重合），垂直于AE的一条直线MN分别交AB，AE，CD于点M，P，N.小聪过点B作BF∥MN分别交AE，CD于点G，F后，猜想线段EC，DN，MB之间的数量关系为EC＝DN＋MB.他的猜想正确吗？请说明理由.

查看解析收藏纠错

+选题
20. 为了解“停课不停学”过程中学生对网课内容的喜爱程度，某校开展了一次网上问卷调查.随机抽取部分学生，按四个类别统计，其中A表示“很喜欢”，B表示“喜欢”，C表示“一般”，D表示“不喜欢”，并将调查结果绘制成下面两幅不完整的统计图.

请根据图中提供的信息，解决下列问题：

（1）这次共抽取名学生进行统计调查，扇形统计图中D类所在扇形的圆心角度数为；

（2）将条形统计图补充完整；

（3）若该校共有3000名学生，估计该校表示“喜欢”的B类学生大约有多少人？

查看解析收藏纠错

+选题
21. 参照学习函数的过程与方法，探究函数y= $\text{[math]}$ 的图象与性质．
因为y= $\text{[math]}$ ，即y=﹣ $\text{[math]}$ +1，所以我们对比函数y=﹣ $\text{[math]}$ 来探究．
列表：
x
…
﹣4
﹣3
﹣2
﹣1
﹣ $\text{[math]}$
       $\text{[math]}$
1
2
3
4
…
y=﹣ $\text{[math]}$
…
       $\text{[math]}$
       $\text{[math]}$
1
2
4
﹣4
﹣1
1
﹣ $\text{[math]}$
﹣ $\text{[math]}$
…
y= $\text{[math]}$
…
       $\text{[math]}$
       $\text{[math]}$
2
3
5
﹣3
﹣1
0
       $\text{[math]}$
       $\text{[math]}$
…
描点：在平面直角坐标系中，以自变量x的取值为横坐标，以y= $\text{[math]}$ 相应的函数值为纵坐标，描出相应的点，如图所示：

（1）请把y轴左边各点和右边各点，分别用一条光滑曲线顺次连接起来；

（2）观察图象并分析表格，回答下列问题：
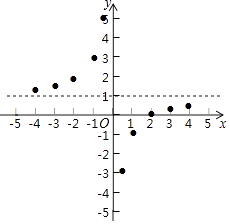
①当x＜0时，y随x的增大而；（填“增大”或“减小”）
②y= $\text{[math]}$ 的图象是由y=﹣ $\text{[math]}$ 的图象向平移个单位而得到；
③图象关于点中心对称．（填点的坐标）

（3）设A（x₁ ， y₁），B（x₂ ， y₂）是函数y= $\text{[math]}$ 的图象上的两点，且x₁+x₂=0，试求y₁+y₂+3的值．

查看解析收藏纠错

+选题
22. 已知：在△ABC中，AB＝AC，点D为BC边的中点，点F是AB边上一点，点E在线段DF的延长线上，∠BAE＝∠BDF，点M在线段DF上，∠ABE=∠DBM.

（1）如图1，当∠ABC＝45°时，求证：AE＝ $\text{[math]}$ MD；

（2）如图2，当∠ABC＝60°时，
①直接写出线段AE，MD之间的数量关系；

②延长BM到P，使MP＝BM，连接CP，若AB＝7，AE＝ $\text{[math]}$ ，探求sin∠PCB的值.

查看解析收藏纠错

+选题

23. 为了抗击新冠病毒疫情，全国人民众志成城，守望相助.春节后某地一水果购销商安排15辆汽车装运A，B，C三种水果120吨销售，所得利润全部捐赠湖北抗疫.已知按计划15辆汽车都要装满且每辆汽车只能装同一种水果，每种水果所用车辆均不少于3辆，汽车对不同水果的运载量和每吨水果销售获利情况如下表.

水果品种	A	B	C
汽车运载量（吨/辆）	10	8	6
水果获利（元/吨）	800	1200	1000

（1）设装运A种水果的车辆数为x辆，装运B种水果车辆数为y辆，根据上表提供的信息，

①求y与x之间的函数关系式；

②设计车辆的安排方案，并写出每种安排方案；

（2）若原有获利不变的情况下，当地政府按每吨50元的标准实行运费补贴，该经销商打算将获利连同补贴全部捐出.问应采用哪种车辆安排方案，可以使这次捐款数w（元）最大化？捐款w（元）最大是多少？

查看解析收藏纠错

+选题

24. 在平面直角坐标系xOy中，已知点P是反比例函数 $\text{[math]}$ 图象上一个动点，以P为圆心的圆始终与y轴相切，设切点为A.

（1）如图1，⊙P运动到与x轴相切，设切点为K，试判断四边形OKPA的形状，并说明理由.

（2）如图2，⊙P运动到与x轴相交，设交点为B，C.当四边形ABCP是菱形时，
①求过点A，B，C三点的抛物线解析式；

②在过A，B，C三点的抛物线上是否存在点M，使△MBP的面积是菱形ABCP面积的 $\text{[math]}$ ？若存在，直接写出所有满足条件的M点的坐标；若不存在，试说明理由.

查看解析收藏纠错

+选题

湖北省荆州市2020年九年级调研考试数学试卷

一、选择题

二、填空题

三、解答题

相关试卷收起∨

湖北省荆州市2020年九年级调研考试数学试卷

一、选择题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨