江苏省常州市天宁区正衡中学2019年九年级数学中考二模试卷

1. 在平面直角坐标系中，点P（–2，3）关于原点对称的点Q的坐标为（）

A . （2，–3） B . （2，3） C . （3，–2） D . （–2，–3）

查看解析收藏纠错

+选题
2. 如果三角形满足一个角是另一个角的3倍，那么我们称这个三角形为“智慧三角形”．下列各组数据中，能作为一个智慧三角形三边长的一组是（）

A . 1，2，3 B . 1，1， $\text{[math]}$ C . 1，1， $\text{[math]}$ D . 1，2， $\text{[math]}$

查看解析收藏纠错

+选题
3. 某次射击训练中，一个小组的成绩如下表所示：

环数

7

8

9

人数

2

3

已知该小组的平均成绩为8.1环，那么成绩为8环的人数是（）

A . 4 B . 5 C . 6 D . 7

查看解析收藏纠错

+选题
4. 如果反比例函数 $\text{[math]}$ 的图象如图所示，那么二次函数 $\text{[math]}$ 的图象大致为（）

A . B . C . D .

查看解析收藏纠错

+选题
5. 如图，若△ABC和△DEF的面积分别为S₁、S₂ ，则（）

A . S₁= $\text{[math]}$ S₂ B . S₁= $\text{[math]}$ S₂ C . S₁=S₂ D . S₁= $\text{[math]}$ S₂

查看解析收藏纠错

+选题
6. 如图，⊙O的内接△ABC的外角∠ACE的平分线交⊙O于点D.DF⊥AC，垂足为F，DE⊥BC，垂足为E.给出下列4个结论：①CE＝CF；②∠ACB＝∠EDF；③DE是⊙O的切线；④ $\text{[math]}$ .其中一定成立的是（）

A . ①②③ B . ②③④ C . ①③④ D . ①②④

查看解析收藏纠错

+选题
7. 方程 $\text{[math]}$ 的正根的个数为（）

A . 0个 B . 1个 C . 2个 D . 3个

查看解析收藏纠错

+选题
8. 某校数学课外小组，在坐标纸上为学校的一块空地设计植树方案如下：第k棵树种植在点P_k(x_k ， y_k)处，其中x₁＝1，y₁＝2，当k≥2时，x_k＝x_k_﹣₁+1﹣5（[ $\text{[math]}$ ]﹣[ $\text{[math]}$ ]），y_k＝y_k_﹣₁+[ $\text{[math]}$ ]﹣[ $\text{[math]}$ ]，[a]表示非负实数a的整数部分，例如[2.6]＝2，[0.2]＝0.按此方案，第2017棵树种植点的坐标为（）

A . (5，2017) B . (6，2016) C . (1，404) D . (2，404)

查看解析收藏纠错

+选题

9. 计算： $\text{[math]}$ .

查看解析收藏纠错

+选题
10. 已知一个圆锥的侧面积是底面积的2倍，圆锥的母线长为2，则圆锥的底面半径是.

查看解析收藏纠错

+选题
11. 一元二次方程x²﹣3x﹣4=0与x²+4x-5=0的所有实数根之和等于

查看解析收藏纠错

+选题
12. 已知关于x的不等式组 $\text{[math]}$ 有3个整数解，则a的取值范围是.

查看解析收藏纠错

+选题
13. 将量角器按如图所示的方式放置在三角形纸片上，使点C在半圆圆心上，点B在半圆上，边AB、AC分别交圆于点E、F，点B、E、F对应的读数分别为160°、70°、50°，则∠A的度数为.

查看解析收藏纠错

+选题
14. 如图所示，点A₁、A₂、A₃在x轴上，且OA₁=A₁A₂=A₂A₃ ，分别过点A₁、A₂、A₃作y轴的平行线，与反比例函数y= $\text{[math]}$ （x＞0）的图象分别交于点B₁、B₂、B₃ ，分别过点B₁、B₂、B₃作x轴的平行线，分别与y轴交于点C₁、C₂、C₃ ，连接OB₁、OB₂、OB₃ ，若图中三个阴影部分的面积之和为 $\text{[math]}$ ，则k=.

查看解析收藏纠错

+选题
15. 如图，抛物线y＝ax²+bx+c与x轴交于点A(﹣1，0)，顶点坐标为C(1，k)，与y轴的交点在(0，2)、(0，3)之间（不包含端点），则k的取值范围是.

查看解析收藏纠错

+选题
16. 如图，网格的小正方形的边长均为1，小正方形的顶点叫做格点.△ABC的三个顶点都在格点上，那么∠ABC的正切值是.

查看解析收藏纠错

+选题
17. 在平面直角坐标系中，A点坐标为(1，0)，C点坐标为(7，0)，若点P在直线y＝kx+3上运动时，只存在一个点P使∠APC＝90°，则k的值是

查看解析收藏纠错

+选题
18. 已知线段AB＝12，C、D是AB上两点，且AC＝DB＝2，P是线段CD上一动点，在AB同侧分别作等边三角形APE和等边三角形PBF，G为线段EF的中点，点P由点C移动到点D时，G点移动的路径长度为

查看解析收藏纠错

+选题

19. 计算（ $\text{[math]}$ ）⁰+（﹣ $\text{[math]}$ ）^﹣²+4cos30°﹣| $\text{[math]}$ |

查看解析收藏纠错

+选题
20. 解下列方程

（1） $\text{[math]}$

（2）（x﹣4）（x+2）＝﹣9

查看解析收藏纠错

+选题
21. 如图，已知点E，F分别是平行四边形ABCD的边BC，AD上的中点.

（1）写出AE与CF的关系，请证明；

（2）当∠BAC等于多少度时，四边形AECF是菱形，请说明理由.

查看解析收藏纠错

+选题
22. 已知，如图，在坡顶A处的同一水平面上有一座古塔BC，数学兴趣小组的同学在斜坡底P处测得该塔的塔顶B的仰角为45°，然后他们沿着坡度为1：2.4的斜坡AP攀行了26米，在坡顶A处又测得该塔的塔顶B的仰角为76°.求：
坡顶A到地面PO的距离；古塔BC的高度（结果精确到1米）.

（参考数据：sin76°≈0.97，cos76°≈0.24，tan76°≈4.01）

查看解析收藏纠错

+选题
23. 某商场将进价40元一个的某种商品按50元一个售出时，每月能卖出500个.商场想了两个方案来增加利润：
方案一：提高价格，但这种商品每个售价涨价1元，销售量就减少10个；

方案二：售价不变，但发资料做广告.已知当这种商品每月的广告费用为m(千元)时，每月销售量将是原销售量的p倍，且p = .

试通过计算，请你判断商场为赚得更大的利润应选择哪种方案？请说明你判断的理由！

查看解析收藏纠错

+选题
24. 如图，⊙O是△ABC的外接圆，AB是直径，作OD∥BC与过点A的切线交于点D，连接DC并延长交AB的延长线于点E．

（1）求证：DE是⊙O的切线；

（2）若AE=6，CE=2 $\text{[math]}$ ，求线段CE、BE与劣弧BC所围成的图形面积．（结果保留根号和π）

查看解析收藏纠错

+选题
25. 如图

【定义】若一个四边形恰好关于其中一条对角线所在的直线对称，则我们将这个四边形叫做镜面四边形.

（1）【理解】下列说法是否正确
①平行四边形是一个镜面四边形

②镜面四边形的面积等于对角线积的一半.

（2）如图（1），请你在4×4的网格（每个小正方形的边长为1）中画出一个镜面四边形，使它图（1）的顶点在格点上，且有一边长为 $\text{[math]}$ .

（3）【应用】如图（2），已知镜面四边形ABCD，∠BAD＝60°，∠ABC＝90°，AB≠BC，P是AD上一点，AE⊥BP的延长线上取一点F，使EF＝BE，连接AF，作∠FAD的平分线AG交BF于G，CM⊥BF于M，连接CG.
①求∠EAG的度数.

②比较BM与EG的大小，并说明理由.

查看解析收藏纠错

+选题
26. 用如图①，②所示的两个直角三角形（部分边长及角的度数在图中已标出），完成以下两个探究问题：

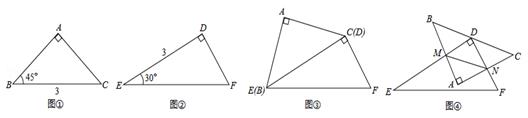
探究一：将以上两个三角形如图③拼接（BC和ED重合），在BC边上有一动点P.

（1）当点P运动到∠CFB的角平分线上时，连接AP，求线段AP的长；

（2）当点P在运动的过程中出现PA=FC时，求∠PAB的度数.
探究二：如图④，将△DEF的顶点D放在△ABC的BC边上的中点处，并以点D为旋转中心旋转△DEF，使△DEF的两直角边与△ABC的两直角边分别交于M、N两点，连接MN.在旋转△DEF的过程中，△AMN的周长是否存在有最小值？若存在，求出它的最小值；若不存在，请说明理由.

查看解析收藏纠错

+选题
27. 如图，在平面直角坐标系xOy中，抛物线 $\text{[math]}$ （ $\text{[math]}$ ）与x轴交于A，B两点（点A在点B的左侧），经过点A的直线l： $\text{[math]}$ 与y轴负半轴交于点C，与抛物线的另一个交点为D，且CD=4AC.

（1）直接写出点A的坐标，并求直线l的函数表达式（其中k，b用含a的式子表示）；

（2）点E是直线l上方的抛物线上的动点，若△ACE的面积的最大值为 $\text{[math]}$ ，求a的值；

（3）设P是抛物线的对称轴上的一点，点Q在抛物线上，以点A，D，P，Q为顶点的四边形能否成为矩形？若能，求出点P的坐标；若不能，请说明理由.

查看解析收藏纠错

+选题

江苏省常州市天宁区正衡中学2019年九年级数学中考二模试卷

一、单选题

二、填空题

三、解答题

相关试卷收起∨

环数	7	8	9
人数	2		3

江苏省常州市天宁区正衡中学2019年九年级数学中考二模试卷

一、单选题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨