修改时间:2022-10-12 浏览次数:95 类型:复习试卷
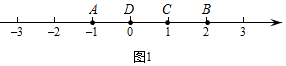
例如;如图1,点 表示的数为-1,点
表示的数为2.表示1的点
到点
的距离是2,到点
的距离是1,那么点
是
的美好点;又如,表示0的点
到点
的距离是1,到点
的距离是2,那么点
就不是
的美好点,但点
是
的美好点.
如图2, ,
为数轴上两点,点
所表示的数为
,点
所表示的数为
.
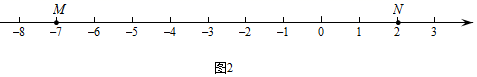
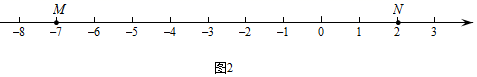
试题篮