修改时间:2022-04-08 浏览次数:144 类型:复习试卷

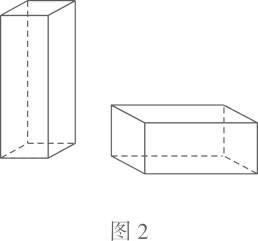
①两种裁法共生产A型板材 ▲ 张,B型板材 ▲ 张.
②能否在做成若干个上述的两种无盖礼品盒后,恰好把①中的A型板材和B型板材用完?若能,则竖式无盖礼品盒与横式无盖礼品盒分别做了几个?若不能,则最多能做成竖式和横式两种无盖礼品盒共多少个?并直接写出此时做成的横式无盖礼品盒的个数.
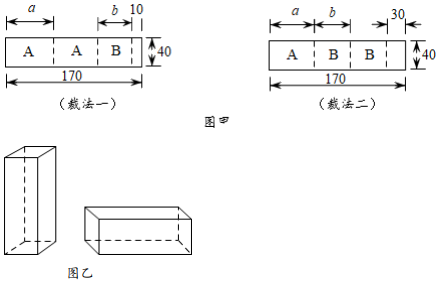
①两种裁法共生产A型板材张,B型板材张;
②能否在做成若干个上述的两种无盖礼品盒后,恰好把①中的A型板材和B型板材用完?若能,则竖式无盖礼品盒与横式无盖礼品盒分别做了几个?若不能,则最多能做成竖式和横式两种无盖礼品盒共多少个?并直接写出此时做成的横式无盖礼品盒的个数.
|
制作成品 |
所需工人(人) |
每个工人每月所需布料(米) |
每件所需布料(米) |
成品售价(元/件) |
平均每制作1米消耗的成本(元) |
|
上衣 |
| 300 | 1.5 | 900 | 200 |
| 裤子 | | 600 | 1 | 300 | 100 |
|
制作的利润 |
不超过200万元的部分 |
超过200万元但不超过250万元的部分 |
超过250万元的部分 |
|
提成比例 |
5% |
m% |
20% |
若该公司给工人发放的9月奖金总额为11.28万元,11月和12月该公司获得的总利润为500万元,11月和12月给员工的奖金总额共为49万元,且12月的利润比11月的利润大,求12月该服装公司的利润.
李老师:“平安客运公司有60座和45座两种型号的客车可供租用,60座客车每辆每天的租金比45座的贵200元.”
小芳:“我们八年级师生上个星期在这个客运公司租了4辆60座和2辆45座的客车到滁州市琅琊山,一天的租金共计5600元.”
小明:“我们七年级师生租用2辆60座和5辆45座的客车正好坐满.”
根据以上对话,解答下列问题:
若A、B、C为数轴上三点,若点C到A的距离是点C到B的距离2倍,我们就称点C是(A,B)的好点.
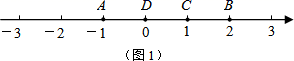
例如,如图1,点A表示的数为-1,点B表示的数为2.表示1的点C到点A的距离是2,到点B的距离是1,那么点C是(A,B)的好点;又如,表示0的点D到点A的距离是1,到点B的距离是2,那么点D就不是(A,B)的好点,但点D是(B,A)的好点.
知识运用:
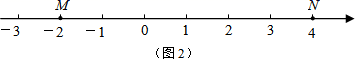
在点M和点N中间,数所表示的点是(M,N)的好点;

请完成填空(余料作废).
方法①:只裁成为0.8米的用料时,最多可裁7根;
方法②:先裁下1根2.5米长的用料,余下部分最多能裁成为0.8米长的用料根;
方法③:先裁下2根2.5米长的用料,余下部分最多能裁成为0.8米长的用料1根.
| 体积(立方米/件) | 质量(吨/件) | |
| | 0.8 | 0.5 |
| | 2 | 1 |
①按车收费:每辆车运输货物到目的地收费600元;
②按吨收费:每吨货物运输到目的地收费200元.
现要将(1)中商品一次或分批运输到目的地,如果两种收费方式可混合使用,商贸公司应如何选择运送、付费方式,使其所花运费最少,最少运费是多少元?

当A灯转动5秒时,两灯的光束AM′和BP′到达如图①所示的位置,试问AM′和BP′是否平行?请说明理由;
试题篮