修改时间:2024-07-13 浏览次数:205 类型:中考模拟
你知道“皮克定理”吗?
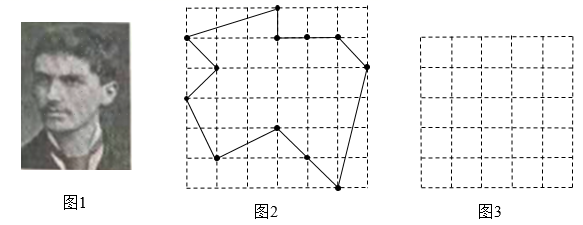
“皮克定理”是奥地利数学家皮克(如图1)发现的一个计算点阵中多边形的面积公式.在一张方格纸上,上面画着纵横两组平行线,相邻平行线之间的距离都相等,这样两组平行线的交点,就是所谓格点.一个多边形的顶点如果全是格点,这个多边形就叫做格点多边形.有趣的是,这种格点多边形的面积计算起来很方便,只要数一下图形边线上的点的数目及图内的点的数目,就可用公式算出.即 ,其中a表示多边形内部的点数,b表示多边形边界上的点数,S表示多边形的面积.(利用图2中的多边形可以验证)这个公式是奥地利数学家皮克在1899年发现的,被称为“皮克定理”.
任务:

①图中2016-2022年全球智能家居市场规模的中位数是 ▲ 亿美元;
②试计算2020-2021年市场规模的增长率(精确到 );
③请你根据图表信息简单描述智能家居的市场规模情况,并对未来市场做出预测;
|
|
|
|
|
W.门窗系统 |
X.音箱系统 |
Q.安防系统 |
|
在平行四边形 办法一: 以点B为圆心, 办法二: 连接 |
任务:
“旋转”即物体绕一个点或一个轴做圆周运动.在中国古典专著《百喻经·口诵乘船法而不解用喻》中记载:“船盘回旋转,不能前进.”而图形旋转即:在平面内,将一个图形绕一点按某个方向转动一个角度,这样的运动叫做图形的旋转,这个定点叫做旋转中心,转动的角叫做旋转角.综合实践课上,“睿智”小组专门探究了正方形的旋转,情况如下:在正方形 中,点O是线段
上的一个动点,将正方形
绕点O顺时针旋转得到正方形
(点
,
,
,
分别是点A,B,C,D的对应点).设旋转角为
(
).
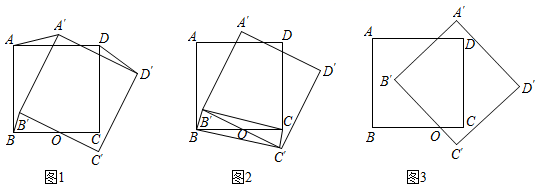
如图1,若点O是 中点,在正方形
绕点旋转过程中,连接
,
,
,则线段
与
的数量关系是;线段
与
的数量关系是.
如图2,在(1)的条件下,在正方形 绕点
旋转过程中,顺次连接点B,
,C,
,B.判断四边形
的形状,并说明理由.
如图3,若 ,在正方形
绕点O顺时针旋转的过程中,设直线
交线段
于点P.连接
,并过点
作
于点Q.请你补全图形,并直接写出
的值.
试题篮