山西省太原市2019-2020学年八年级上学期数学期中考试试卷

1. 下列实数中的无理数是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
2. 4的算术平方根是 $\text{[math]}$ 　　 $\text{[math]}$

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 2

查看解析收藏纠错

+选题
3. 下列各组数中，能作为直角三角形三边长的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
4. 下列计算结果正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
5. 已知一次函数 $\text{[math]}$ ( $\text{[math]}$ 为常数)的图象经过平面直角坐标系的第一、二、三象限，则下列结论一定正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
6. 在平面直角坐标系中，已知一次函数 $\text{[math]}$ 的图象经过 $\text{[math]}$ 两点，则 $\text{[math]}$ 的大小关系为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 无法确定

查看解析收藏纠错

+选题
7. 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，以 $\text{[math]}$ 的三边为边分别向外作等边三角形 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ 的面积分别是10和4，则 $\text{[math]}$ 的面积是（）

A . 4 B . 6 C . 8 D . 9

查看解析收藏纠错

+选题
8. 对于一次函数 $\text{[math]}$ (k，b为常数)，下表中给出5组自变量及其对应的函数值：

$\text{[math]}$

……

-1

0

1

2

3

$\text{[math]}$

……

-2

1

4

8

10

……

其中只有1个函数值计算有误，则这个错误的函数值是( )

A . 1 B . 4 C . 8 D . 10

查看解析收藏纠错

+选题
9. 为比较 $\text{[math]}$ 与 $\text{[math]}$ 的大小，小亮进行了如下分析后作一个直角三角形，使其两直角边的长分别为 $\text{[math]}$ 与 $\text{[math]}$ ，则由的股定理可求得其斜边长为 $\text{[math]}$ .根据“三角形三边关系”，可得 $\text{[math]}$ .小亮的这一做法体现的数学思想是（）

A . 分类讨论思想 B . 方程思想 C . 类比思想 D . 数形结合思想

查看解析收藏纠错

+选题
10. 棱长分别为 $\text{[math]}$ 的两个正方体如图放置，点A，B，E在同一直线上，顶点G在棱BC上，点P是棱 $\text{[math]}$ 的中点.一只蚂蚁要沿着正方体的表面从点A爬到点P，它爬行的最短距离是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题

11. 把 $\text{[math]}$ 化成最简二次根式为.

查看解析收藏纠错

+选题
12. 已知点 $\text{[math]}$ 在一次函数 $\text{[math]}$ 的图象上，则点 $\text{[math]}$ 的坐标为.

查看解析收藏纠错

+选题
13. 在平整的路面上，某型号汽车紧急利车后滑行sm，一般地有公式 $\text{[math]}$ ，其中v表标刹车前汽车的速度(单位： $\text{[math]}$ ).一次行驶中汽车紧急刹车后滑行的距离 $\text{[math]}$ ，则这辆汽车刹车前的速度 $\text{[math]}$ km/h

查看解析收藏纠错

+选题
14. 《算法统宗》中有一道“荡秋干”的问题，其译文为：“有一架秋千，当它静止时，踏板上一点A离地1尺，将它往前推送10尺(水平距离)时，点A对应的点B就和某人一样高，若此人的身高为5尺，秋干的绳索始终拉得很直，试问绳素有多长？”根据上述条件，秋干绳索长为尺.

查看解析收藏纠错

+选题
15. 如图，在 $\text{[math]}$ 中 $\text{[math]}$ 于点D，点P是线段AD上一个动点，过点P作 $\text{[math]}$ 于点E，连接PB，则 $\text{[math]}$ 的最小值为.

查看解析收藏纠错

+选题

16. 计算

（1） $\text{[math]}$

（2） $\text{[math]}$

（3） $\text{[math]}$

（4） $\text{[math]}$ .

查看解析收藏纠错

+选题
17. 如图，在平面直角坐标系中， $\text{[math]}$ 的三个顶点的坐标分别为 $\text{[math]}$ .

（1）请在如图的坐标系中画出 $\text{[math]}$ .

（2）在如图的坐标系中，画出 $\text{[math]}$ 关于 $\text{[math]}$ 轴对称的 $\text{[math]}$ ，并直接写出 $\text{[math]}$ 三个顶点的坐标.

查看解析收藏纠错

+选题
18. 在一次综合实践活动中，老师让同学们测量公园里凉亭A，B之间的距离(A，B之间有水池，无法直接测量).智慧小组的同学们在公园里选了凉亭C，D，测得 $\text{[math]}$ ， $\text{[math]}$ .请你根据上述数据求出A，B之间的距离.

查看解析收藏纠错

+选题
19. 如图，已知一次函数 $\text{[math]}$ 的图象与 $\text{[math]}$ 轴， $\text{[math]}$ 轴分别交于A，B两点，点 $\text{[math]}$ 在该函数的图象上，连接OC．求点A，B的坐标和 $\text{[math]}$ 的面积.

查看解析收藏纠错

+选题
20. 如图，在 $\text{[math]}$ 中， $\text{[math]}$ .点 $\text{[math]}$ 在 $\text{[math]}$ 轴的正半轴上，边AB在 $\text{[math]}$ 轴上(点A在点B的左侧).

（1）求点C的坐标.

（2）点D是BC边上一点，点E是AB边上一点，且点E和点C关于AD所在直线对称，直接写出点D坐标.

查看解析收藏纠错

+选题
21. 2019年10月1日是中华人民共和国成立70周年纪念日，红色旅游成为旅游热点.小王要和朋友们去某红色景点旅游，其门票零售价为80元/张.国庆节期间，景点推出优惠活动，方案1：门票一律九折优惠；方案2：对10人以内(含10人)购门票不优惠，超过10人超出部分八折优惠.设小王一行参加旅游的人数为x(人)，购买门票费用为y(元).

（1）小王分别写出方案1和方案2购买门票的费用y(元)与旅游人数x(人)之间的函数表达式如下，请你将空缺部分补充完整：
$\text{[math]}$ $\text{[math]}$ ； $\text{[math]}$

（2）小王一行共有40人一起去该景点旅游，通过计算，判断选择哪种方案更省钱？

查看解析收藏纠错

+选题
22. 阅读材料：
材料一：两个含有二次根式的非零代数式相乘，如果它们的积不含二次根式，那么这两个代数式互为有理化因式.

例如： $\text{[math]}$ ，我们称 $\text{[math]}$ 的一个有理化因式是 $\text{[math]}$ 的一个有理化因式是 $\text{[math]}$ .

材料二：如果一个代数式的分母中含有二次根式，通常可将分子、分母同乘分母的有理化因式，使分母中不含根号，这种变形叫做分母有理化.

例如： $\text{[math]}$ ，

$\text{[math]}$

请你仿照材料中的方法探索并解决下列问题：

（1） $\text{[math]}$ 的有理化因式为， $\text{[math]}$ 的有理化因式为.(均写出一个即可)

（2）将下列各式分母有理化(要求写出变形过程)：
① $\text{[math]}$ .

② $\text{[math]}$ .

（3）请从下列A，B两题中任选一题作答，我选择题.
A计算： $\text{[math]}$ 的结果为.

B计算： $\text{[math]}$ 的结果为.

查看解析收藏纠错

+选题
23. 如图1，已知直线 $\text{[math]}$ 与 $\text{[math]}$ 轴， $\text{[math]}$ 轴分别交于A，B两点，过点B在第二象限内作 $\text{[math]}$ 且 $\text{[math]}$ ，连接 $\text{[math]}$ .

（1）求点C的坐标.

（2）如图2，过点C作直线 $\text{[math]}$ 轴交AB于点D，交 $\text{[math]}$ 轴于点E，
请从下列A，B两题中任选一题作答，我选择题
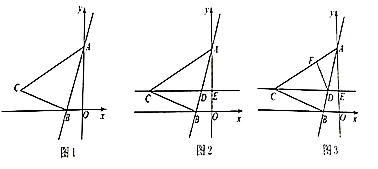
A．①求线段CD的长.
②在坐标平面内，是否存在点M(除点B外)，使得以点M，C，D为顶点的三角形与 $\text{[math]}$ 全等？若存在，请直接写出所有符合条件的点M的坐标：若不存在，请说明理由.
B．①如图3，在图2的基础上，过点D作 $\text{[math]}$ 于点F，求线段DF的长.
②在坐标平面内，是否存在点M(除点F外)，使得以点M，C，D为顶点的三角形与 $\text{[math]}$ 全等？若存在，请直接写出所有符合条件的点M的坐标；若不存在，请说明理由.

查看解析收藏纠错

+选题

山西省太原市2019-2020学年八年级上学期数学期中考试试卷

一、单选题

二、填空题

三、解答题

相关试卷收起∨

$\text{[math]}$	……	-1	0	1	2	3
$\text{[math]}$	……	-2	1	4	8	10	……

山西省太原市2019-2020学年八年级上学期数学期中考试试卷

一、单选题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨