甘肃省兰州市2019年中考数学试卷

修改时间：2019-08-01 浏览次数：1049 类型：中考真卷编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、单选题

1. -2019的相反数是（）

A . $\text{[math]}$ B . 2019 C . -2019 D . $\text{[math]}$

查看解析收藏纠错

+选题
2. 如图，直线a，b被直线c所截，a//b，∠1=80°，则∠2=（）

A . 130° B . 120° C . 110° D . 100°

查看解析收藏纠错

+选题
3. 计算 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . 3 D . $\text{[math]}$

查看解析收藏纠错

+选题
4. 剪纸是中国特有的民间艺术.在如涂所示的四个剪纸图案中.既是轴对称图形又是中心对称图形的是（）

A . B . C . D .

查看解析收藏纠错

+选题
5. $\text{[math]}$ 是关于 $\text{[math]}$ 的一元二次方程 $\text{[math]}$ 的解，则 $\text{[math]}$ （）

A . -2 B . -3 C . 4 D . -6

查看解析收藏纠错

+选题
6. 如图，四边形ABCD内接于⊙O，若∠A=40°，则∠C=（）

A . 110° B . 120° C . 135° D . 140°

查看解析收藏纠错

+选题
7. 化简： $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
8. 已知 $\text{[math]}$ ∽ $\text{[math]}$ ，AB=8，A`B`=6，则 $\text{[math]}$ （）

A . 2 B . $\text{[math]}$ C . 3 D . $\text{[math]}$

查看解析收藏纠错

+选题
9. 《九章算术》是中国古代数学著作之一，书中有这样一个问题：五只雀、六只燕共重一斤，雀重燕轻，互换其中一只，恰好一样重.问：每只雀、燕的重量各为多少?设一只雀的重量为x斤，一只燕的重量为y斤，则可列方程组为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
10. 如图，在平面直角坐标系 $\text{[math]}$ 中，将四边形ABCD先向下平移，再向右平移得到四边形A₁B₁C₁D₁ ，已知A(-3，5)，B(-4，3)，A₁(3，3)，则点B₁坐标为（）

A . (1，2) B . (2，1) C . (1，4) D . (4，1)

查看解析收藏纠错

+选题
11. 已知点A(1，y₁),B(2,y₂)在抛物线y=-(x+1)²+2上，则下列结论正确的是（）

A . 2>y₁>y₂ B . 2>y₂>y₁ C . y₁>y₂>2 D . y₂>y₁>2

查看解析收藏纠错

+选题
12. 如图，边长为 $\text{[math]}$ 的正方形ABCD的对角线AC与BD交于点O，将正方形ABCD沿直线DF折叠，点C落在对角线BD上的点E处，折痕DF交AC于点M，则OM=（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题

二、填空题

13. 因式分解：a³+2a²+a=．

查看解析收藏纠错

+选题
14. 在 $\text{[math]}$ 中，AB=AC， $\text{[math]}$ ，则 :∠B=。

查看解析收藏纠错

+选题
15. 如图，矩形0ABC的顶点B在反比例函数 $\text{[math]}$ 的图像上， $\text{[math]}$ ，则 K=。

查看解析收藏纠错

+选题
16. 如图，矩形ABCD，∠BAC=60°以点A为圆心，以任意长为半径作弧分别交AB、AC于M，N两点，再分别以点M，N为圆心，以大于 $\text{[math]}$ MN的长为半径作弧交于点P，作射线AP交BC于点E，若BE=1，则矩形ABCD的面积等于.

查看解析收藏纠错

+选题

三、解答题

17. 计算： $\text{[math]}$

查看解析收藏纠错

+选题
18. 化简： $\text{[math]}$

查看解析收藏纠错

+选题
19. 解不等式组： $\text{[math]}$

查看解析收藏纠错

+选题
20. 如图，AB=DE，BF=EC，∠B=∠E，求证：AC//DF.

查看解析收藏纠错

+选题
21. 2019年5月，以“寻根国学，传承文明”为主题的兰州市第三届“国学少年强一国学知识挑战赛”总决赛拉开帷幕，小明晋级了总决赛.比赛过程分两个环节，参赛选手须在每个环节中各选择一道题目。
第一环节：写字注音、成语故事、国学常识、成语接龙(分别用A₁ ， A₂ ， A₃ ， A₄表示)；

第二环节：成语听写、诗词对句、经典通读(分别用B₁ ， B₂ ， B₃表示)

（1）请用树状图或列表的方法表示小明参加总决赛抽取题目的所有可能结果

（2）求小明参加总决赛抽取题目都是成语题目(成语故事、成语接龙、成语听写)的概率。

查看解析收藏纠错

+选题
22. 如图，AC=8，分别以A，C为圆心，以长度5为半径作弧，两条弧分别相交于点B和D，依次连接A，B，C，D，连接BD交AC于点0.

（1）判断四边形ABCD的形状并说明理由

（2）求BD的长.

查看解析收藏纠错

+选题
23. 如图，在平面直角坐标系xOy中，反比例函数 $\text{[math]}$ 的图象过等边三角形BOC的顶点B， OC=2，点A在反比例函数图象上，连接AC，AO.

（1）求反比例函数 $\text{[math]}$ 的表达式；

（2）若四边形ACBO的面积是 $\text{[math]}$ ，求点A的坐标.

查看解析收藏纠错

+选题
24. 为了解某校八年级学生一门课程的学习情况，小佳和小丽分别对八年级1班和2班本门课程的期末成绩进行了调查分析.小佳对八年级1班全班学生(25名)的成绩进行分析，过程如下收集、整理数据：
表一：

表二：

小丽用同样的方式对八年级2班全班学生(25 名)的成绩进行分析，变数据如下：

根据以上信息，解决下列问题：

（1）已知八年级1班学生的成绩在80≤x＜90这一组的数据如下：
85，87，88，80，82，85，83，85，87，85
根据上述数据，将表二补充完整；

（2）你认为哪个班级的成绩更为优异?请说明理由

查看解析收藏纠错

+选题
25. 某数学课题研究小组针对兰州市住房窗户“如何设计遮阳篷”这-课题进行了探究，过程如下：
问题提出：
如图1是某住户窗户上方安装的遮阳蓬，要求设计的遮阳篷既能最大限度地遮挡夏天炎热的阳光，又能最大限度地使冬天温暖的阳光射入室内.
方案设计：
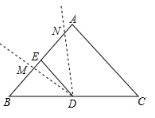
如图2，该数学课题研究小组通过调查研究设计了垂直于墙面AC的遮阳篷CD
数据收集：
通过查阅相关资料和实际测量：兰州市一年中，夏至这一天的正午时刻，太阳光线DA与遮阳篷CD的夹角∠ADC最大(∠ADC=77.44°)：冬至这一天的正午时刻，太阳光线DB与遮阳篷CD的夹角
∠BDC最小(∠BDC=30.56°)；窗户的高度AB=2m
问题解决：
根据上述方案及数据，求遮阳篷CD的长.
(结果精确到0.1m，参考数据：sin30.56°≈0.51 ，cos30.56°≈0.86， tan30.56°≈0.59，sin77.44°≈0.98，cos77.44°≈0.22，tan77.44°≈4.49)

查看解析收藏纠错

+选题
26. 如图，在△ABC中，AB=AC=6cm，BC=8cm，点D为BC的中点，BE=DE.将∠BDE绕点D顺时针旋转 $\text{[math]}$ 度( $\text{[math]}$ )，角的两边分别交直线AB于M，N两点，设B，M两点间的距离为 $\text{[math]}$ cm，M，N两点间的距离为 $\text{[math]}$ cm。
小涛根据学习函数的经验，对函数 $\text{[math]}$ 随自变量 $\text{[math]}$ 的变化而变化的规律进行了探究，下面是小涛的探究过程，请补充完整.

（1）列表：下表的已知数据是B，M两点间的距离x进行取点、画图、测量，分别得到了y与x的几组对应值：
x/m 0 0.30 0.50 1.00 1.50 2.00 2.50 3.00 3.50 3.68 3.81 3.90 3.93 4.10
y/m
2.88
2.81 2.69 2.67 2.80 3.15
3.85 5.24 6.01
6.71 7.27 7.44 8.87
请你通过计算，补全表格；

（2）描点、连线：在平面直角坐标系xOy中，描出表中各组数值所对应的点(x，y)，并画出函数y关于x的图象：

（3）探究性质：随着自变量x的不断增大，函数y的变化趋势：

（4）解决问题：当MN=2BM时，BM的长度大约是cm(保留两位小数).

查看解析收藏纠错

+选题
27. 主题学习
通过对下面数学模型的研究学习，解决（1）（2）题
【模型呈现】
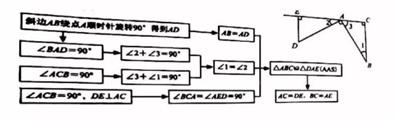
如图，在Rt△ABC中，∠ACB=90°，将斜边AB绕点A顺时针旋转90°得到AD，过点D作DE⊥AC于点E，可以推理得到△ABC≌△DAE，进而得到AC=DE，BC=AE
我们把这个数学模型称为“K型”，
推理过程如下：

【模型应用】
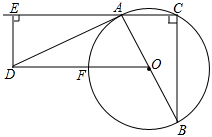
如图，Rt△ABC内接于⊙O，∠ACB=90°，BC=2.将斜边AB绕点A顺时针旋转一定角度得到AD，过点D作DE⊥AC于点E，∠DAE=∠ABC，DE=1，连接DO交⊙O于点F.

（1）求证：AD是⊙O的切线；

（2）接FC交AB于点G，连接FB，求证：FG²=GO·GB.

查看解析收藏纠错

+选题
28. 二次函数 $\text{[math]}$ 的图象交x轴于A(-1， 0)，B(4， 0)两点，交y轴于点C.动点M从点A出发，以每秒2个单位长度的速度沿AB方向运动，过点M作MN⊥x轴交直线BC于点N，交抛物线于点D，连接
AC.设运动的时间为t秒.

（1）求二次函数 $\text{[math]}$ 的表达式：

（2）连接BD，当 $\text{[math]}$ 时，求△DNB的面积：

（3）在直线MN上存在一点P，当△PBC是以∠BPC为直角的等腰直角三角形时，求此时点D的坐标；

（4）当 $\text{[math]}$ 时，在直线MN上存在一点Q，使得∠AQC+∠OAC=90°，求点Q的坐标，

查看解析收藏纠错

+选题

x/m	0	0.30	0.50	1.00	1.50	2.00	2.50		3.00	3.50	3.68	3.81	3.90	3.93	4.10
y/m		2.88	2.81	2.69	2.67	2.80	3.15		3.85	5.24	6.01	6.71	7.27	7.44	8.87

甘肃省兰州市2019年中考数学试卷

一、单选题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨