备战2024年中考数学细点逐一突破真题训练第12章全等三角形（2）

1. 如图， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .求证： $\text{[math]}$ .

查看解析收藏纠错

+选题
2. 下列判断错误的是（）

A . 有两角和一边对应相等的两个三角形全等 B . 三条边对应相等的两个三角形全等 C . 全等三角形对应边上的高相等 D . 三个角对应相等的两个三角形全等

查看解析收藏纠错

+选题
3. 如图，两个全等的直角三角形重叠在一起，将其中的一个三角形沿着点 $\text{[math]}$ 到 $\text{[math]}$ 的方向平移到 $\text{[math]}$ 的位置， $\text{[math]}$ ， $\text{[math]}$ ，平移距离为 $\text{[math]}$ ，则阴影部分面积为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
4. 已知：如图，点E、F在CD上，且 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．
求证： $\text{[math]}$ ≌ $\text{[math]}$ ．

查看解析收藏纠错

+选题
5. 同学们在做题时，经常用到“在直角三角形中， $\text{[math]}$ 角所对的直角边等于斜边的一半”这个定理，下面是两种添加辅助线的证明方法，请你选择一种进行证明.
已知：在 $\text{[math]}$ 中， $\text{[math]}$ ，
求证： $\text{[math]}$ .
方法一：如图1，在AB上取一点 $\text{[math]}$ ，使得 $\text{[math]}$ ，连接CD.
方法二：如图2，延长BC到 $\text{[math]}$ ，使得 $\text{[math]}$ ，连接AD.
我选择方法 ▲ .
证明：

查看解析收藏纠错

+选题

6. 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，点B在第四象限时，则点B的坐标为．

查看解析收藏纠错

+选题
7. 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ．点 $\text{[math]}$ 在线段 $\text{[math]}$ 上运动（ $\text{[math]}$ 不与 $\text{[math]}$ ， $\text{[math]}$ 重合），连接 $\text{[math]}$ ，作 $\text{[math]}$ ， $\text{[math]}$ 交线段 $\text{[math]}$ 于点 $\text{[math]}$ ．
⑴当 $\text{[math]}$ 时， $\text{[math]}$ °；
⑵当 $\text{[math]}$ 时， $\text{[math]}$ ．

查看解析收藏纠错

+选题
8. 如图，CD是经过 $\text{[math]}$ 顶点C的一条直线， $\text{[math]}$ ， E ， F分别是直线CD上两点，且 $\text{[math]}$ .
图1 图2 图3

（1）若直线CD经过 $\text{[math]}$ 的内部，且E ， F在射线CD上.
①如图1，当 $\text{[math]}$ 时，证明： $\text{[math]}$ .
②如图2，若 $\text{[math]}$ ，当 $\text{[math]}$ 与 $\text{[math]}$ 满足什么数量关系时，①中的结论仍然成立，并说明理由.

（2）如图3，若直线CD经过 $\text{[math]}$ 的外部， $\text{[math]}$ ，猜想EF ， BE ， AF三条线段的数量关系，并证明.

查看解析收藏纠错

+选题
9. 【模型介绍】
如图 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 于点 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 于点 $\text{[math]}$ ．则 $\text{[math]}$ ．我们把这个数学模型称为“ $\text{[math]}$ 字”模型或“一线三等角”模型．
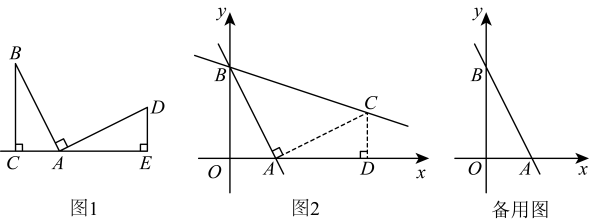
【模型应用】
在平面直角坐标系中，直线 $\text{[math]}$ 与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ，与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ．

（1）如图 $\text{[math]}$ ，将直线 $\text{[math]}$ 绕点 $\text{[math]}$ 逆时针旋转 $\text{[math]}$ ，得到直线 $\text{[math]}$ ，求直线 $\text{[math]}$ 的表达式．下面是小明的想法，请你帮助完成．
小明想利用“一线三等角”模型解决这个问题．如图，过点 $\text{[math]}$ 作 $\text{[math]}$ 的垂线交 $\text{[math]}$ 于点 $\text{[math]}$ ，再过点 $\text{[math]}$ 作 $\text{[math]}$ 轴的垂线，垂足为 $\text{[math]}$ ，可求出点 $\text{[math]}$ 的坐标为，从而求得直线 $\text{[math]}$ 的表达式为．

（2）若将直线 $\text{[math]}$ 绕点 $\text{[math]}$ 顺时针旋转 $\text{[math]}$ ，所得直线的表达式为．

（3）点 $\text{[math]}$ 是线段 $\text{[math]}$ 上的一个动点，点 $\text{[math]}$ 是线段 $\text{[math]}$ 上一动点，若 $\text{[math]}$ 是等腰直角三角形，且 $\text{[math]}$ ，则点 $\text{[math]}$ 的坐标是．

查看解析收藏纠错

+选题
10.

（1）某学习小组在探究三角形全等时，发现了下面这种典型的基本图形.如图1，已知：在△ABC中，∠BAC＝90°，AB＝AC ，直线l经过点A ， BD⊥直线l ， CE⊥直线l ，垂足分别为点D、E.证明：DE＝BD+CE.

（2）组员小刘想，如果三个角不是直角，那结论是否会成立呢？如图2，将（1）中的条件改为：在△ABC中，AB＝AC ， D、A、E三点都在直线l上，并且有∠BDA＝∠AEC＝∠BAC＝α，其中α为任意锐角或钝角.请问结论DE＝BD+CE是否成立？如成立，请你给出证明；若不成立，请说明理由.

（3）数学老师赞赏了他们的探索精神，并鼓励他们运用这个知识来解决问题：如图3，过△ABC的边AB、AC向外作正方形ABDE和正方形ACFG ， AH是BC边上的高，延长HA交EG于点I ，求证：I是EG的中点.

查看解析收藏纠错

+选题

11. 八（2）班数学兴趣小组在一次活动中进行了探究实验活动，请你和他们一起活动吧．
[发现问题]他们在探究实验活动中遇到了下面的问题：如图1， $\text{[math]}$ 是 $\text{[math]}$ 的中线，若 $\text{[math]}$ ，求 $\text{[math]}$ 的取值范围．
[探究方法]他们通过探究发现，延长 $\text{[math]}$ 至点E ，使 $\text{[math]}$ ，连接 $\text{[math]}$ ．可以证出 $\text{[math]}$ ，利用全等三角形的性质可将已知的边长与 $\text{[math]}$ 转化到 $\text{[math]}$ 中，进而求出 $\text{[math]}$ 的取值范围．
方法小结：从上面的思路可以看出，解决问题的关键是将中线 $\text{[math]}$ 延长一倍，构造出全等三角形，我们把这种方法叫做“倍长中线法”．
[问题解决]

（1）请你利用上面解答问题的思路方法，写出求 $\text{[math]}$ 的取值范围的过程．

（2）如图2， $\text{[math]}$ 是 $\text{[math]}$ 的中线，且 $\text{[math]}$ ，求证： $\text{[math]}$ ．

查看解析收藏纠错

+选题
12. 如下是某书中某一页的部分内容：
如图，在 $\text{[math]}$ 中， $\text{[math]}$ 是边 $\text{[math]}$ 的中点，过点 $\text{[math]}$ 画直线 $\text{[math]}$ ，使 $\text{[math]}$ ，交 $\text{[math]}$ 的延长线于点 $\text{[math]}$ ，求证： $\text{[math]}$ .
证明： $\text{[math]}$ （已知）
$\text{[math]}$ ， $\text{[math]}$ （两直线平行，内错角相等）.
在 $\text{[math]}$ 与 $\text{[math]}$ 中，
$\text{[math]}$ ， $\text{[math]}$ （已证），
$\text{[math]}$ （已知），
$\text{[math]}$ ，
$\text{[math]}$ （全等三角形的对应边相等）.
图（1）图（2）图（3）

（1）【方法应用】如图（1），在 $\text{[math]}$ 中， $\text{[math]}$ ，则 $\text{[math]}$ 边上的中线 $\text{[math]}$ 长度的取值范围是；

（2）【猜想证明】如图（2），在四边形 $\text{[math]}$ 中， $\text{[math]}$ ，点 $\text{[math]}$ 是 $\text{[math]}$ 的中点，若 $\text{[math]}$ 是 $\text{[math]}$ 的平分线，试猜想线段 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 之间的数量关系，并证明你的猜想.

（3）【拓展延伸】如图（3），已知 $\text{[math]}$ ，点 $\text{[math]}$ 是 $\text{[math]}$ 的中点，点 $\text{[math]}$ 在线段 $\text{[math]}$ 上， $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ，直接写出线段 $\text{[math]}$ 的长。

查看解析收藏纠错

+选题

13. 已知，正方形的四条边相等，四个角是直角．如图，点E，F分别在正方形 $\text{[math]}$ 的两边 $\text{[math]}$ 和 $\text{[math]}$ 上， $\text{[math]}$ 与 $\text{[math]}$ 相交于点G ，且 $\text{[math]}$ ．

（1）求证： $\text{[math]}$ ；

（2）若 $\text{[math]}$ ，求 $\text{[math]}$ 的长度．

查看解析收藏纠错

+选题
14. $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 是直线 $\text{[math]}$ 上的一个动点，连接 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 的垂线，垂足为点 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 的平行线交直线 $\text{[math]}$ 于点 $\text{[math]}$ ．

（1）如图1，当点 $\text{[math]}$ 为 $\text{[math]}$ 中点时，请直接写出线段 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系．

（2）如图2，当点 $\text{[math]}$ 在线段 $\text{[math]}$ 上 $\text{[math]}$ 不与 $\text{[math]}$ ， $\text{[math]}$ 重合 $\text{[math]}$ ，请探究线段 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 之间的数量关系(要求：写出发现的结论，并说明理由)．

（3）如图3，当点 $\text{[math]}$ 在线段 $\text{[math]}$ 延长线上，请探究线段 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 之间的数量关系(要求：画出图形，写出发现的结论，并说明理由)．

（4）当点 $\text{[math]}$ 在线段 $\text{[math]}$ 延长线上，请直接写出线段 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 之间的数量关系．

查看解析收藏纠错

+选题

15. 如图，点D是△ABC三条角平分线的交点，∠ABC＝68°，若AB+BD＝AC ，则∠ACB的度数为．

查看解析收藏纠错

+选题
16. 如图， $\text{[math]}$ 中， $\text{[math]}$ 、 $\text{[math]}$ 的角平分线 $\text{[math]}$ 、 $\text{[math]}$ 交于点 $\text{[math]}$ ，延长 $\text{[math]}$ 、 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 则下列结论中正确的个数（）
$\text{[math]}$ 平分 $\text{[math]}$ ； $\text{[math]}$ ； $\text{[math]}$ ； $\text{[math]}$ ．

A . $\text{[math]}$ 个 B . $\text{[math]}$ 个 C . $\text{[math]}$ 个 D . $\text{[math]}$ 个

查看解析收藏纠错

+选题
17. 【教材呈现】如图是华师版八年级上册数学教材第 $\text{[math]}$ 页的部分内容．
角平分线的性质定理，角平分线上的点到角两边的距离相等．
已知：如图 $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 的平分线，点 $\text{[math]}$ 是 $\text{[math]}$ 上的任何一点， $\text{[math]}$ ， $\text{[math]}$ ，垂足分别为点 $\text{[math]}$ 和点 $\text{[math]}$ ．
求证： $\text{[math]}$ ．
请写出完整的证明过程： $\text{[math]}$

（1）请根据教材内容，结合图 $\text{[math]}$ ，写出“角平分线的性质定理”完整的证明过程．

（2）【应用】如图 $\text{[math]}$ ，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 平分 $\text{[math]}$ ， $\text{[math]}$ 于点 $\text{[math]}$ ，点 $\text{[math]}$ 在 $\text{[math]}$ 上， $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的长为．

（3）【拓展】如图 $\text{[math]}$ ，在 $\text{[math]}$ 中， $\text{[math]}$ 平分 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ 于点 $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的面积．

查看解析收藏纠错

+选题
18. 综合与实践

（1）问题初探
如图1，在等腰直角△ABC中，∠B=90°，AB=BC，将△ABD沿着AD折叠得到△AED，AB的对应边AE落在AC上，点B的对应点为E，折痕AD交BC于点D.
求证：AC=AB+BD；

（2）方法迁移
如图2，AD是△ABC的角平分线，∠C=2∠B.求证：AB=AC+DC；

（3）问题拓展
如图3，在△ABC中，∠ABC=2∠C，AD是△ABC的外角的平分线，交CB的延长线于点D.请你直接写出线段AC，AB，BD之间的数量关系.

查看解析收藏纠错

+选题

19. 如图，点 $\text{[math]}$ 是等边 $\text{[math]}$ 内一点， $\text{[math]}$ 是 $\text{[math]}$ 外的一点， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ≌ $\text{[math]}$ ， $\text{[math]}$ ，连接 $\text{[math]}$ ．

（1）求证： $\text{[math]}$ 是等边三角形；

（2）当 $\text{[math]}$ 时，试判断 $\text{[math]}$ 的形状，并说明理由；

（3）探究：当 $\text{[math]}$ 为多少度时， $\text{[math]}$ 是等腰三角形．

查看解析收藏纠错

+选题
20. 已知，如图①，在 $\text{[math]}$ 和 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$

（1）求证：① $\text{[math]}$ ；② $\text{[math]}$ ；

（2）如图②，在 $\text{[math]}$ 和 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则AC与BD的等量关系为． $\text{[math]}$ 的大小为．（直接写出结果，不需要证明）

查看解析收藏纠错

+选题
21. 如图，A、B、C在同一条直线上， $\text{[math]}$ 和 $\text{[math]}$ 均为等边三角形， $\text{[math]}$ 、 $\text{[math]}$ 分别交 $\text{[math]}$ 、 $\text{[math]}$ 于点M、N，下列结论中：① $\text{[math]}$ ， ② $\text{[math]}$ ， ③ $\text{[math]}$ ， ④ $\text{[math]}$ ， ⑤ $\text{[math]}$ 平分 $\text{[math]}$ ，其中正确的有．（填序号）

查看解析收藏纠错

+选题
22. 如图，在 $\text{[math]}$ 和 $\text{[math]}$ 中， $\text{[math]}$ 三点在同一条直线上，连接 $\text{[math]}$ ．以下四个结论中：① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ ；④ $\text{[math]}$ ，正确的个数是（）．

A . 1个 B . 2个 C . 3个 D . 4个

查看解析收藏纠错

+选题
23. 综合与实践、数学模型可以用来解决一类问题，是数学应用基本途径．通过探究图形的变化规律，再结合其他数学知识的内在联系，最终可以获得宝贵的数学经验，并将其运用到更广阔的数学天地．

（1）发现问题：如图1，在 $\text{[math]}$ 与 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， B ， F ， C三点在一条直线上，连接EF交AB于点D ．则线段 $\text{[math]}$ 与 $\text{[math]}$ 、 $\text{[math]}$ 的数量关系是 ▲ ，并说明理由．

（2）类比探究：如图2，在 $\text{[math]}$ 中， $\text{[math]}$ ，以AC为边，作 $\text{[math]}$ ，满足 $\text{[math]}$ ， E为BC上一点，连接AE ， $\text{[math]}$ ，连接 $\text{[math]}$ ，求证： $\text{[math]}$ ．

查看解析收藏纠错

+选题
24. 如图，△ABC是等腰直角三角形，∠ACB＝90°，AC=BC=2 $\text{[math]}$ ， D在线段BC上，E是线段AD上一点．现以CE为直角边，C为直角顶点，在CE的下方作等腰直角△ECF，连接BF．

（1）如图1，求证：∠CAE＝∠CBF；

（2）当A、E、F三点共线时，如图2，
①求证：∠DFB＝90°；
②若BF＝2，求AF的长．

查看解析收藏纠错

+选题

25. 如图，在四边形 $\text{[math]}$ 中， $\text{[math]}$ 平分 $\text{[math]}$ ，且 $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ 一定等于（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
26. 如图 $\text{[math]}$ 是正三角形， $\text{[math]}$ 是顶角 $\text{[math]}$ 的等腰三角形，以D为顶点作一个60°角，角的两边分别交AB、AC边于M、N两点，连接MN ．

（1）探究：写出线段BM、MN、NC之间的数量关系，并说明理由．

（2）若点M、N分别是AB、CA延长线上的点，其它条件不变，直接写出线段BM、MN、NC之间的数量关系（不用说明理由），并在图中画出图形．

查看解析收藏纠错

+选题
27. 我们定义：如图1，在四边形ABCD中，如果 $\text{[math]}$ ， $\text{[math]}$ ，对角线BD平分 $\text{[math]}$ ，我们称这种四边形为“分角对补四边形”.
图1
图2
图3

（1）特例感知：如图1，在“分角对补四边形”ABCD中，当 $\text{[math]}$ 时，根据教材中一个重要性质直接可得 $\text{[math]}$ ，这个性质是；（填序号）
①垂线段最短：②垂直平分线的性质；③角平分线的性质；④三角形内角和定理

（2）猜想论证：如图2，当 $\text{[math]}$ 为任意角时，猜想DA与DC的数量关系，并给予证明；

（3）探究应用：如图3，在等腰 $\text{[math]}$ 中， $\text{[math]}$ ， BD平分 $\text{[math]}$ ，
求证： $\text{[math]}$ .

查看解析收藏纠错

+选题
28.

（1）如图 $\text{[math]}$ ，在四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 分别是边 $\text{[math]}$ 上的点，且 $\text{[math]}$ ，线段 $\text{[math]}$ 之间的关系是；（不需要证明）

（2）如图 $\text{[math]}$ ，在四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 分别是边 $\text{[math]}$ 上的点，且 $\text{[math]}$ ，（ $\text{[math]}$ ）中的结论是否仍然成立？若成立，请证明．若不成立，请写出它们之间的数量关系，并证明．

（3）如图 $\text{[math]}$ ，在四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 分别是边 $\text{[math]}$ 延长线上的点，且 $\text{[math]}$ ，（ $\text{[math]}$ ）中的结论是否仍然成立？若成立，请证明．若不成立，请写出它们之间的数量关系，并证明．

查看解析收藏纠错

+选题
29.

（1）【问题背景】如图1，点E、F分别在正方形 $\text{[math]}$ 的边 $\text{[math]}$ 、 $\text{[math]}$ 上， $\text{[math]}$ ，连接 $\text{[math]}$ ，则有 $\text{[math]}$ ，试说明理由；

（2）【迁移应用】如图2，四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点E、F分别在边 $\text{[math]}$ 、 $\text{[math]}$ 上， $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ 都不是直角，且 $\text{[math]}$ ，试探究 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 之间的数量关系；

（3）【联系拓展】如图3，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点D、E均在边 $\text{[math]}$ 上，且 $\text{[math]}$ ，猜想 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 满足的等量关系．（直接写出结论，不需要证明）．

查看解析收藏纠错

+选题
30.

（1）如图1，在四边形ABCD中，AB＝AD ， ∠B＝∠D＝90°，E、F分别是边BC、CD上的点，且∠EAF＝ $\text{[math]}$ ∠BAD ，线段EF、BE、FD之间的关系是；（不需要证明）

（2）如图2，在四边形ABCD中，AB＝AD ， ∠B+∠D＝180°，E、F分别是边BC、CD上的点，且∠EAF＝ $\text{[math]}$ ∠BAD ，（1）中的结论是否仍然成立？若成立，请证明．若不成立，请写出它们之间的数量关系，并证明．

（3）如图3，在四边形ABCD中，AB＝AD ， ∠B+∠D＝180°，E、F分别是边BC、CD延长线上的点，且∠EAF＝ $\text{[math]}$ ∠BAD ，（1）中的结论是否仍然成立？若成立，请证明．若不成立，请写出它们之间的数量关系，并证明．

查看解析收藏纠错

+选题

31. 如图，在等边 $\text{[math]}$ 中，点D ， E分别在边 $\text{[math]}$ 上，且 $\text{[math]}$ 与 $\text{[math]}$ 相交于点P ， $\text{[math]}$ 于点Q

（1）求证： $\text{[math]}$ ；

（2）求 $\text{[math]}$ 的度数；

（3）若 $\text{[math]}$ ，求 $\text{[math]}$ 的长．

查看解析收藏纠错

+选题
32. 如图，在等边三角形 $\text{[math]}$ 中，点M为 $\text{[math]}$ 边上任意一点，延长 $\text{[math]}$ 至点N ，使 $\text{[math]}$ ，连接 $\text{[math]}$ 交 $\text{[math]}$ 于点P ， $\text{[math]}$ 于点H ．

（1）求证： $\text{[math]}$ ；

（2）若 $\text{[math]}$ ，求线段 $\text{[math]}$ 的长．

查看解析收藏纠错

+选题

备战2024年中考数学细点逐一突破真题训练第12章全等三角形（2）

一、基础类型（平移，翻折，轴对称）

二、一线三等角型

三、倍长中线模型

四、十字架全等模型

五、角平分线模型

六、手拉手模型

七、半角模型（对角互补）

八、含30度直角三角形

相关试卷收起∨

备战2024年中考数学细点逐一突破真题训练第12章全等三角形（2）

一、基础类型（平移，翻折，轴对称）

二、一线三等角型

三、倍长中线模型

四、十字架全等模型

五、角平分线模型

六、手拉手模型

七、半角模型（对角互补）

八、含30度直角三角形

相关试卷 收起∨

相关试卷收起∨