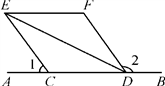
如图,已知EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD(请填空)

解:∵EF∥AD
∴∠2={#blank#}1{#/blank#}({#blank#}2{#/blank#})
又∵∠1=∠2
∴∠1=∠3({#blank#}3{#/blank#})
∴AB∥{#blank#}4{#/blank#}({#blank#}5{#/blank#})
∴∠BAC+{#blank#}6{#/blank#}=180°({#blank#}7{#/blank#})
∵∠BAC=70°({#blank#}8{#/blank#})
∴∠AGD={#blank#}9{#/blank#}({#blank#}10{#/blank#})