2022年苏科版初中数学《中考一轮复习》专题四图形的认识 4.2 三角形

1. 下列长度的三条线段首尾顺次相接，能够组成三角形的是（　　）

A . 3，5，10 B . 5，7，12 C . 4，4，8 D . 8，8，10

查看解析收藏纠错

+选题
2. 已知三角形三个内角的度数之比为3：3：4，则这个三角形是（）

A . 等腰三角形 B . 直角三角形 C . 钝角三角形 D . 等边三角形

查看解析收藏纠错

+选题
3. 若一个三角形的三边长为a，b，c，且满足a²-2ab+b²+ac-bc =0，则这个三角形是（）

A . 直角三角形 B . 等边三角形 C . 等腰三角形 D . 等腰直角三角形

查看解析收藏纠错

+选题
4. 在计算一个多边形的内角和时，由于粗心少算了1个内角，其和等于1180°，则少算的这个角的度数是（）

A . 60 B . 70 C . 80 D . 90

查看解析收藏纠错

+选题
5. 如图，把圆分成六等分，经过各分点作圆的切线，以相邻切线的交点为顶点的图形是这个圆的外切正六边形， $\text{[math]}$ 的半径是R，它的外切正六边形的边长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
6. 如图，BM是△ABC的角平分线，D是BC边上的一点，连接AD，使AD=DC，且∠BAD=120°，则∠AMB=（）

A . 30° B . 25° C . 22.5° D . 20°

查看解析收藏纠错

+选题
7. 如图，∠MON=90°，矩形ABCD的顶点A、B分别在边OM，ON上，当B在边ON上运动时，A随之在边OM上运动，矩形ABCD的形状保持不变，其中AB=2，BC=1，运动过程中，点D到点O的最大距离为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ 5 D . $\text{[math]}$

查看解析收藏纠错

+选题
8. 如图，在 $\text{[math]}$ 中， ∠ACB=90°， $\text{[math]}$ cm， $\text{[math]}$ cm. $\text{[math]}$ 是 $\text{[math]}$ 边上的一个动点，连接 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 于 $\text{[math]}$ ，连接 $\text{[math]}$ ，在点 $\text{[math]}$ 变化的过程中，线段 $\text{[math]}$ 的最小值是（）

A . 1 B . $\text{[math]}$ C . 2 D . $\text{[math]}$

查看解析收藏纠错

+选题
9. 如图，AB＝AD＝6，∠A＝60°，点C在∠DAB内部且∠C＝120°，则CB＋CD的最大值（）

A . 4 $\text{[math]}$ B . 8 C . 10 D . 6 $\text{[math]}$

查看解析收藏纠错

+选题
10. 如图，一个适当大的正六边形，它的一个顶点与一个边长为定值的小正六边形ABCDEF的中心O重合，且与边AB、CD相交于G、H．将多边形OGBCH的面积记为S，三条线段GB、BC、CH的长度之和记为l，在大正六边形绕点O旋转过程中，下列说法正确的是（）．

A . S变化，l不变 B . S不变，l变化 C . S变化，l变化 D . S与l均不变

查看解析收藏纠错

+选题

11. 如图，在△ABC中，点D、E分别是AB、AC边的中点，若BC＝6cm．刚线段DE＝cm．

查看解析收藏纠错

+选题
12. 如图，直线m $\text{[math]}$ n．若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的大小为度．

查看解析收藏纠错

+选题
13. 如图，在△ABC中，∠B = 60°，∠C = 40°，AE平分∠BAC，AD⊥BC，垂足为点D，那么∠DAE =度．

查看解析收藏纠错

+选题
14. 如图，在△ABC中，∠ACB为钝角，把边AC绕点A沿逆时针方向旋转90°得AD，把边BC绕点B沿顺时针方向旋转90°得BE，作DM⊥AB于点M，EN⊥AB于点N，若AB＝5，EN＝2，则DM＝.

查看解析收藏纠错

+选题
15. 如图，点 $\text{[math]}$ 分别是等边三角形 $\text{[math]}$ 的边 $\text{[math]}$ 的点，且 $\text{[math]}$ 与 $\text{[math]}$ 相交于点 $\text{[math]}$ ．则 $\text{[math]}$ 的度数为．

查看解析收藏纠错

+选题
16. 如图，G为正方形ABCD的边AD上的一个动点，AE⊥BG，CF⊥BG，垂足分别为点E、F，已知AD=4，则AE²+CF²＝

查看解析收藏纠错

+选题
17. 如图，在△ABC中，已知D，E，F分别为BC，AD，CE的中点，且S_△ABC＝8cm² ，则图中阴影部分△BEF的面积等于cm² ．

查看解析收藏纠错

+选题
18. 如图， $\text{[math]}$ 为 $\text{[math]}$ 的 $\text{[math]}$ 边上的点、且 $\text{[math]}$ ，中线 $\text{[math]}$ 被 $\text{[math]}$ 截得的三线段为 $\text{[math]}$ ，则 $\text{[math]}$

查看解析收藏纠错

+选题

19. 如图，AD、BF相交于点O，点E、C在BF上，BE=FC，AC=DE，AB=DF，求证：四边形ABDF是平行四边形。

查看解析收藏纠错

+选题
20. 如图，▱ABCD的对角线AC，BD相交于点O，点E、F在AC上，且AF=CE．
求证：BE=DF．

查看解析收藏纠错

+选题
21. 如图，在等腰 $\text{[math]}$ ABC中，AB=AC=6cm，∠B=30°，点D在BC边上由点C向点B匀速运动（点D不与点B ， C重合），速度为2cm/s，连接AD ，作∠ADE=30°，DE交线段AC于点E ．

（1）在此运动过程中，∠BDA逐渐变（填“大”或“小”）；D点运动到图1位置时，∠BDA=75°，则∠BAD=°．

（2）点D运动3s后到达图2位置，则CD=cm．此时 $\text{[math]}$ ABD和 $\text{[math]}$ DCE是否全等，请说明理由．

（3）在点D运动过程中， $\text{[math]}$ ADE的形状也在变化．当 $\text{[math]}$ ADE是等腰三角形时，∠BDA的度数为．

查看解析收藏纠错

+选题
22. 如图所示，△ABC是边长为6的等边三角形，P是AC边上一动点，由点A向点C运动(与A，C不重合)，Q是CB延长线上的一点，与点P同时以相同的速度由点B向CB延长线方向运动(Q不与B重合)，过点P作PE⊥AB于点E，连接PQ交AB于点D．

（1）当∠BQD=30°时，求AP的长．

（2）试说明：在运动过程中，点D是线段PQ的中点．

（3）在运动过程中，线段ED的长是否发生变化？如果不变，求出线段ED的长；如果变化，请说明理由．

查看解析收藏纠错

+选题
23. 请阅读下列材料：
问题：在四边形ABCD中，M是BC边的中点，且∠AMD=90°

（1）如图1，若AB与CD不平行，试判断AB+CD与AD之间的数量关系；
小雪同学的思路是：延长DM至E使DM=ME，连接AE，BE，构造全等三角形，经过推理使问题得到解决请你参考小雪的思路，在图1中把图形补充完整，并直接写出上面问题AB+CD与AD之间的数量关系：

（2）如图2，若在原条件的基础上，增加AM平分∠BAD，（1）中结论还成立吗？若不成立，写出AB+CD与AD之间的数量关系，并证明．

查看解析收藏纠错

+选题
24. 如图1，△ABC和△DCE都是等边三角形.
探究发现

（1） △BCD与△ACE是否全等？若全等，加以证明；若不全等，请说明理由.
拓展运用

（2）若B、C、E三点不在一条直线上，∠ADC＝30°，AD＝3，CD＝2，求BD的长.

（3）若B、C、E三点在一条直线上（如图2），且△ABC和△DCE的边长分别为1和2，求△ACD的面积及AD的长.

查看解析收藏纠错

+选题
25.

（1）如图①在 $\text{[math]}$ ABC中，点O是∠ABC和∠ACB平分线的交点，若∠A=α，则∠BOC=（用α表示）；如图②∠CBO= $\text{[math]}$ ∠ABC，∠BCO= $\text{[math]}$ ∠ACB，∠A=α，则∠BOC=（用α表示）

（2）扩展探究：
如图③，∠CBO= $\text{[math]}$ ∠DBC，∠BCO= $\text{[math]}$ ∠ECB，∠A=α，求∠BOC的度数（用α表示），并说明理由.

查看解析收藏纠错

+选题
26. 如图

（1）方法呈现：
如图①：在 $\text{[math]}$ 中，若 $\text{[math]}$ ， $\text{[math]}$ ，点D为BC边的中点，求BC边上的中线AD的取值范围．

解决此问题可以用如下方法：延长AD到点E使 $\text{[math]}$ ，再连接BE，可证 $\text{[math]}$ ，从而把AB、AC， $\text{[math]}$ 集中在 $\text{[math]}$ 中，利用三角形三边的关系即可判断中线AD的取值范围是，这种解决问题的方法我们称为倍长中线法；

（2）探究应用：
如图②，在 $\text{[math]}$ 中，点D是BC的中点， $\text{[math]}$ 于点D，DE交AB于点E，DF交AC于点F，连接EF，判断 $\text{[math]}$ 与EF的大小关系并证明；

（3）问题拓展：
如图③，在四边形ABCD中， $\text{[math]}$ ，AF与DC的延长线交于点F、点E是BC的中点，若AE是 $\text{[math]}$ 的角平分线．试探究线段AB，AF，CF之间的数量关系，并加以证明．

查看解析收藏纠错

+选题
27. 我们定义：如果一个三角形一条边上的高等于这条边，那么这个三角形叫做“等高底”三角形，这条边叫做这个三角形的“等底”.

（1）概念理解：
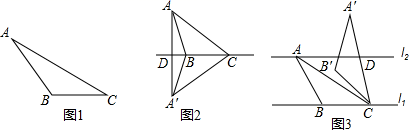
如图1，在△ABC中，AC＝6，DC＝3，∠ACB＝30°，试判断△ABC是否是“等高底”三角形.（填“是”或“否”）

（2）问题探究：
如图2，△ABC是“等高底”三角形，BC是“等底”，作△ABC关于BC所在直线的对称图形得到△A'BC，连接AA'交直线BC于点D.若点B是△AA′C的重心，求 $\text{[math]}$ 的值.

（3）应用拓展：
如图3，已知l₁∥l₂ ， l₁与l₂之间的距离为2，“等高底”△ABC的“等底”BC在直线l₁上，点A在直线l₂上，有一边的长是BC的 $\text{[math]}$ 倍.将△ABC绕点C按顺时针方向旋转45°得到△A'B′C，A′C所在直线交l₂于点D，直接写出CD的值.

查看解析收藏纠错

+选题
28.

（1）问题发现：如图1，已知C为线段AB上一点，分别以线段AC、BC为直角边作等腰直角三角形，∠ACD=90°，CA=CD，CB=CE，连接AE、BD，则AE、BD之间的数量关系为；位置关系为.

（2）拓展探究：如图2，把Rt△ACD绕点C逆时针旋转，线段AE、BD交于点F，则 AE与 BD 之间的关系是否仍然成立?请说明理由.

（3）拓展延伸：如图3，已知AC=CD，BC=CE，∠ACD=∠BCE=90°，连接AB、AE、AD，把线段 AB绕点A旋转，若AB=5，AC=3，请直接写出旋转过程中线段AE的最大值.

查看解析收藏纠错

+选题

2022年苏科版初中数学《中考一轮复习》专题四图形的认识 4.2 三角形

一、单选题

二、填空题

三、综合题

相关试卷收起∨

2022年苏科版初中数学《中考一轮复习》 专题四 图形的认识 4.2 三角形

一、单选题

二、填空题

三、综合题

相关试卷 收起∨

2022年苏科版初中数学《中考一轮复习》专题四图形的认识 4.2 三角形

相关试卷收起∨