陕西省中考数学历年真题模拟题汇编——锐角三角函数与解直角三角形

1. 如图，在矩形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点 E 在边 $\text{[math]}$ 上，且 $\text{[math]}$ .连接 $\text{[math]}$ ，将 $\text{[math]}$ 沿 $\text{[math]}$ 折叠，点 C 的对应点 $\text{[math]}$ 恰好落在边 $\text{[math]}$ 上，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 5

查看解析收藏纠错

+选题
2. 如图，△ABC是⊙O的内接三角形，连接OA、OB、OC.若∠AOB＝40°，∠OBC＝50°，AC＝4，则⊙O的直径为（）

A . $\text{[math]}$ B . 4 C . $\text{[math]}$ D . 8

查看解析收藏纠错

+选题
3. 如图，在▱ABCD中，BC＝6 $\text{[math]}$ ，∠A＝135°，S_▱ABCD＝12 $\text{[math]}$ .若点E、F分别在边BC、AD上，且AF＝CE，∠EFD＝30°，则AF的长为（）

A . $\text{[math]}$ ﹣1 B . 2 $\text{[math]}$ ﹣1 C . 6 $\text{[math]}$ ﹣6 D . 4 $\text{[math]}$ ﹣2

查看解析收藏纠错

+选题
4. 若二次函数y＝ax²+bx+c的图象与x轴有两个交点A和B，顶点为C，且b²﹣4ac＝4，则∠ACB的度数为（）

A . 30° B . 45° C . 60° D . 90°

查看解析收藏纠错

+选题
5. 如图，矩形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 于 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
6. 如图，在矩形 $\text{[math]}$ 中，对角线 $\text{[math]}$ 交点为O，过点O作BD的垂线OE交BC于点E，若 $\text{[math]}$ ，则EC长是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
7. 如图，在平面直角坐标系中，圆P经过点A （0， $\text{[math]}$ ）、O（0，0）、B（1，0），点C在第一象限内的AB上，则∠BCO的度数为（）

A . 60° B . 45° C . 30° D . 15°

查看解析收藏纠错

+选题
8. 如图，在△ABC中，AC＝8，∠ABC＝60°，∠C＝45°，AD⊥BC，垂足为D，∠ABC的平分线交AD于点E，则AE的长为（）

A . $\text{[math]}$ B . 2 $\text{[math]}$ C . $\text{[math]}$ D . 3 $\text{[math]}$

查看解析收藏纠错

+选题
9. 如图，△ABC是⊙O的内接三角形，∠C=30°，⊙O的半径为5，若点P是⊙O上的一点，在△ABP中，PB=AB，则PA的长为（）

A . 5 B . $\text{[math]}$ C . 5 $\text{[math]}$ D . 5 $\text{[math]}$

查看解析收藏纠错

+选题
10.
如图，⊙O的半径为4，△ABC是⊙O的内接三角形，连接OB、OC．若∠BAC与∠BOC互补，则弦BC的长为（）

A . 3 $\text{[math]}$ B . 4 $\text{[math]}$ C . 5 $\text{[math]}$ D . 6 $\text{[math]}$

查看解析收藏纠错

+选题

11. 如图，正方形 $\text{[math]}$ 的边长为 $\text{[math]}$ ，点P在 $\text{[math]}$ 上，连接 $\text{[math]}$ ，则 $\text{[math]}$ 的最大值为.

查看解析收藏纠错

+选题
12. 如图，在平面直角坐标系中，点A在第二象限内，点B在x轴上，∠AOB＝30°，AB＝BO，反比例函数y＝ $\text{[math]}$ (x＜0)的图象经过点A，若S_△AOB＝ $\text{[math]}$ ，则k的值为.

查看解析收藏纠错

+选题
13. 如图，已知平行四边形ABCD中，∠B=60°，AB=12，BC=5，P为AB上任意一点(可以与A、B重合)，延长PD到F，使得DF=PD，以PF、PC为边作平行四边形PCEF，则PE长度的最小值.

查看解析收藏纠错

+选题
14. 如图，线段BC和动点A构成△ABC，∠BAC=120°，BC=3，则△ABC周长的最大值.

查看解析收藏纠错

+选题
15. 如图， $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 于点D，点E是线段CD的一个动点，则 $\text{[math]}$ 的最小值是.

查看解析收藏纠错

+选题
16. 如图，已知在四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则四边形 $\text{[math]}$ 面积的最小值是.

查看解析收藏纠错

+选题
17. 菱形 $\text{[math]}$ 的边 $\text{[math]}$ ， $\text{[math]}$ ，则菱形 $\text{[math]}$ 的面积为.

查看解析收藏纠错

+选题
18. 如图，Rt△AOB中，∠AOB＝90°，顶点A，B分别在反比例函数y＝ $\text{[math]}$ （x＞0）与y＝ $\text{[math]}$ （x＜0）的图象上，则tan∠BAO的值为 .

查看解析收藏纠错

+选题
19. 将一副直角三角板如图放置，点C在FD的延长上，AB∥CF，∠F＝∠ACB＝90°，∠E＝30°，∠A＝45°，AC＝12 $\text{[math]}$ ，则CD的长为.

查看解析收藏纠错

+选题
20. 如图，在梯形 ABCD 中，AD∥BC，BD⊥DC.若 AD＝2，BC＝4，则梯形 ABCD 的面积的最大值为.

查看解析收藏纠错

+选题

21. 2020年我国建成5G基站超60万个，5G建设跑出“中国速度”.某地有一个5G信号塔AB，小敏想用所学的数学知识测量信号塔AB的高度，她选择用树CD和楼房来测量.首先在树的底部D处测得信号塔的顶部A的仰角为42°；然后她站在楼房上的点E处恰好看到树的顶端C、信号塔的顶端A在一条直线上.测得树与楼房的距离DF＝12米，CD＝12米，EF＝6米，已知点B、D、F三点共线，AB⊥BF，CD⊥BF，EF⊥BF，测量示意图如图所示.请根据相关测量信息，求信号塔AB的高度.（参考数据：sin42°≈0.67，cos42°≈0.74，tan42°≈0.90）

查看解析收藏纠错

+选题
22. 小雁塔位于西安市南门外的荐福寺内，与大雁塔同为唐长安城保留至今的重要标志.小莹在数学综合实践活动中，欲利用所学的数学知识对小雁塔的高度进行测量，如图，CD是临时搭建的一个钢架，小莹先测得小雁塔与钢架CD之间的距离AC为43m，然后她站在E点处测得钢架CD的顶端D的仰角为26.7°，转身测得小雁塔AB的顶端B的仰角为47.8°，已知钢架CD的高度为4m，小莹的观测点E距地面的距离EF＝1.5m，且AB⊥AC，EF⊥AC，CD⊥AC，求小雁塔AB的高度.（参考数据：sin47.8°≈0.74，cos47.8°≈0.67，tan47.8°≈1.10，sin26.7°≈0.45，cos26.7°≈0.89，tan26.7°≈0.50）

查看解析收藏纠错

+选题
23. 一座吊桥的钢索立柱 $\text{[math]}$ 两侧各有若干条斜拉的钢索，大致如图所示.小明和小亮想用测量知识测较长钢索 $\text{[math]}$ 的长度，他们测得 $\text{[math]}$ 为30°，由于B、D两点间的距离不易测得，通过探究和测量，发现 $\text{[math]}$ 恰好为45°，点B与点C之间的距离约为16m.已知点B、C、D共线， $\text{[math]}$ .求钢索 $\text{[math]}$ 的长度.（结果保留根号）

查看解析收藏纠错

+选题
24. 如图所示，小明家与小华家住在同一栋楼的同一单元，他俩想测算所住楼对面商业大厦的高MN.他俩在小明家的窗台B处，测得商业大厦顶部N的仰角∠1的度数，由于楼下植物的遮挡，不能在B处测得商业大厦底部M的俯角的度数.于是，他俩上楼来到小华家，在窗台C处测得大厦底部M的俯角∠2的度数，竟然发现∠1与∠2恰好相等.已知A，B，C三点共线，CA⊥AM，NM⊥AM，AB＝31m，BC＝18m，试求商业大厦的高MN.

查看解析收藏纠错

+选题
25. 小明利用刚学过的测量知识来测量学校内一棵古树的高度。一天下午，他和学习小组的同学带着测量工具来到这棵古树前，由于有围栏保护，他们无法到达古树的底部B，如图所示。于是他们先在古树周围的空地上选择一点D，并在点D处安装了测量器DC，测得古树的顶端A的仰角为45°；再在BD的延长线上确定一点G，使DG=5米，并在G处的地面上水平放置了一个小平面镜，小明沿着BG方向移动，当移动带点F时，他刚好在小平面镜内看到这棵古树的顶端A的像，此时，测得FG=2米，小明眼睛与地面的距离EF=1.6米，测倾器的高度CD=0.5米。已知点F、G、D、B在同一水平直线上，且EF、CD、AB均垂直于FB，求这棵古树的高度AB。（小平面镜的大小忽略不计）

查看解析收藏纠错

+选题
26. 某市一湖的湖心岛有一棵百年古树，当地人称它为“乡思柳”，不乘船不易到达，每年初春时节，人们喜欢在“聚贤亭”观湖赏柳．小红和小军很想知道“聚贤亭”与“乡思柳”之间的大致距离，于是，有一天，他们俩带着侧倾器和皮尺来测量这个距离．测量方法如下：如图，首先，小军站在“聚贤亭”的A处，用侧倾器测得“乡思柳”顶端M点的仰角为23°，此时测得小军的眼睛距地面的高度AB为1.7米，然后，小军在A处蹲下，用侧倾器测得“乡思柳”顶端M点的仰角为24°，这时测得小军的眼睛距地面的高度AC为1米．请你利用以上测得的数据，计算“聚贤亭”与“乡思柳”之间的距离AN的长（结果精确到1米）．（参考数据：sin23°≈0.3907，cos23°≈0.9205，tan23°≈0.4245，sin24°≈0.4067，cos24°≈0.9135，tan24°≈0.4452．）

查看解析收藏纠错

+选题

27. 如图，AB是⊙O的直径，CD与⊙O相切于D，作CH⊥AB于H，交⊙O于E.交AD于F，若AE∥CD.

（1）求证：AE＝EF；

（2）若cosC＝ $\text{[math]}$ ，AH＝6，求HF的长.

查看解析收藏纠错

+选题
28. 已知：函数 $\text{[math]}$ 的图象与 $\text{[math]}$ 轴相交于点 A(x₁ ， 0)、B(x₂ ， 0) 两点 $\text{[math]}$ ，与 $\text{[math]}$ 轴相交于点 $\text{[math]}$ ， $\text{[math]}$ .

（1）求抛物线的解析式且写出其顶点坐标；

（2）连结 $\text{[math]}$ ，求 $\text{[math]}$ 的值.

查看解析收藏纠错

+选题
29. 问题提出.

（1）如图①，已知等边 $\text{[math]}$ 的外接圆半径为2，则该等边三角形的边长是；

（2）如图②在正方形ABCD中，E，F分别是AB，BC边上的点，且∠EDF＝45°，将 $\text{[math]}$ 绕点D逆时针旋转90°，得到 $\text{[math]}$ .求证：EF＝CF+AE；

（3）问题解决
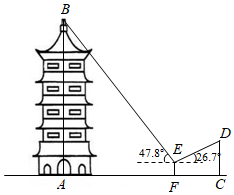
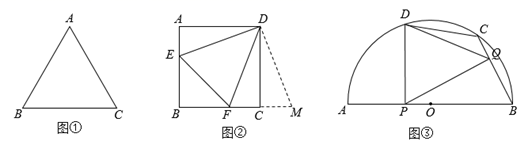
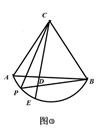
如图③，是一个半圆形广场的示意图，AB为直径，点C、D在 $\text{[math]}$ 上，BC、CD是两条石板路，且AB＝2BC＝2CD＝40cm.现要在直径AB上找一点P，石板路BC上找一点Q，满足∠PDQ＝60°，将 $\text{[math]}$ 区域建成商业活动区，其他区域进行景观绿化.由于附近居民希望景观绿化的面积尽可能的大，按此要求商业活动区的面积要尽可能的小，那么 $\text{[math]}$ 的面积是否存在最小值，若存在，请求出 $\text{[math]}$ 面积的最小值；若不存在，请说明理由.

查看解析收藏纠错

+选题
30. 问题探究

（1）如图①，在△ABC中，AB＝AC，∠B＝30°，AB＝3，则BC的长为；

（2）如图②，四边形ABCD中，DA⊥AB，CB⊥AB，AD＝3，AB＝5，BC＝2，P是边AB上的动点，求PC+PD的最小值；

（3）某山庄有一营地，如图③，营地是由等边△ABC和弦AB与其所对的劣弧围成的弓形组成的，其中AC＝600m， $\text{[math]}$ 所对的圆心角为120°，点D是AB上的一个取水点，AD＝200m，连接CD交 $\text{[math]}$ 于点E.管理员计划在 $\text{[math]}$ 上建一个入口P，在PC、PB上分别建取水点M、N.由于取水点之间需按D→M→N→D的路径铺设水管，因此，为了节约成本要使得线段DM、MN、ND之和最短，试求DM+MN+ND的最小值.

查看解析收藏纠错

+选题
31. 如图，在⨀ $\text{[math]}$ 中，AB为⨀ $\text{[math]}$ 的直径，C为⨀ $\text{[math]}$ 上一点，P是 $\text{[math]}$ 的中点，过点P作AC的垂线，交AC的延长线于点D.

（1）求证：DP是⨀ $\text{[math]}$ 的切线；

（2）若AC=5， $\text{[math]}$ ，求AP的长.

查看解析收藏纠错

+选题

陕西省中考数学历年真题模拟题汇编——锐角三角函数与解直角三角形

一、单选题

二、填空题

三、解答题

四、综合题

相关试卷收起∨

陕西省中考数学历年真题模拟题汇编——锐角三角函数与解直角三角形

一、单选题

二、填空题

三、解答题

四、综合题

相关试卷 收起∨

相关试卷收起∨