北京市丰台区2021年中考数学二模试卷

修改时间：2024-07-13 浏览次数：124 类型：中考模拟编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、单选题

1. 如图是某几何体的三视图，该几何体是（）

A . 圆锥 B . 圆柱 C . 三棱柱 D . 长方体

查看解析收藏纠错

+选题
2. $\text{[math]}$ 年 $\text{[math]}$ 月 $\text{[math]}$ 日凌晨，嫦娥 $\text{[math]}$ 号返回器携带月球样本成功着陆．已知地球到月球的平均距离约为 $\text{[math]}$ 千米．将 $\text{[math]}$ 用科学记数法表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
3. 下列交通标志中，是中心对称图形的是（）

A . 禁止驶入 B . 靠左侧道路行驶 C . 向左和向右转弯 D . 环岛行驶

查看解析收藏纠错

+选题
4. 若 $\text{[math]}$ ，则下列不等式一定成立的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
5. 下列计算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
6. 如图，l₁∥l₂ ，点O在直线l₁上，将三角板的直角顶点放在点O处，三角板的两条直角边与l₂交于A ， B两点，若∠1＝35°，则∠2的度数为（）

A . 35° B . 45° C . 55° D . 65°

查看解析收藏纠错

+选题
7. 学校要举行运动会，小亮和小刚报名参加100米短跑项目的比赛，预赛分A ， B ， C三组进行，小亮和小刚恰好在同一个组的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
8. 某公司新产品上市30天全部售完．图1表示产品的市场日销售量与上市时间之间的关系，图2表示单件产品的销售利润与上市时间之间的关系，下列四个结论中错误的是（）

A . 第30天该产品的市场日销售量最大 B . 第20天至30天该产品的单件产品的销售利润最大 C . 第20天该产品的日销售总利润最大 D . 第20天至30天该产品的日销售总利润逐日增多

查看解析收藏纠错

+选题

二、填空题

9. 若 $\text{[math]}$ 在实数范围内有意义，则x的取值范围是.

查看解析收藏纠错

+选题
10. 若一个多边形的内角和是 $\text{[math]}$ ，则该多边形的边数是.

查看解析收藏纠错

+选题
11. 写出一个比2大且比3小的无理数：．

查看解析收藏纠错

+选题
12. 如图，⊙O是△ABC的外接圆，半径是2，∠BAC＝60°，则 $\text{[math]}$ 的长是．

查看解析收藏纠错

+选题
13. 如图所示的网格是正方形网格，A ， B ， C ， D 是网格线交点，则△ABC与△DBC面积的大小关系为：S_△ABC S_△DBC（填“＞”，“＝”或“＜”）．

查看解析收藏纠错

+选题
14. 随着5G网络技术的发展，市场对5G产品的需求越来越大．为满足市场需求，某大型5G产品生产厂家更新技术后，加快了生产速度．现在平均每天比更新技术前多生产30万件产品，现在生产500万件产品所需的时间与更新技术前生产400万件产品所需时间相同．设更新技术前每天生产x万件，依据题意列出关于x的方程．

查看解析收藏纠错

+选题
15. 已知抛物线 $\text{[math]}$ 与 $\text{[math]}$ 轴的一个交点的横坐标大于1且小于2，则m的取值范围是．

查看解析收藏纠错

+选题
16. 某单位有10000名职工，想通过验血的方式筛查出某种病毒的携带者．如果对每个人的血样逐一化验，需要化验10000次．统计专家提出了一种化验方法：随机地按5人一组分组，然后将各组5个人的血样混合再化验．如果混合血样呈阴性，说明这5个人全部阴性；如果混合血样呈阳性，说明其中至少有一个人呈阳性，就需要对这组的每个人再分别化验一次．假设携带该病毒的人数占0.05%．回答下列问题：

（1）按照这种化验方法是否能减少化验次数（填“是”或“否”）；

（2）按照这种化验方法至多需要次化验，就能筛查出这10000名职工中该种病毒的携带者．

查看解析收藏纠错

+选题

三、解答题

17. 计算： $\text{[math]}$ ．

查看解析收藏纠错

+选题
18. 解不等式组： $\text{[math]}$

查看解析收藏纠错

+选题
19. 如图，AB＝AD ， AC＝AE ， ∠BAE＝∠DAC ．求证：∠C＝∠E ．

查看解析收藏纠错

+选题
20. 已知 $\text{[math]}$ ，求代数式 $\text{[math]}$ 的值．

查看解析收藏纠错

+选题
21. 下面是小融设计的“过直线外一点作圆与这条直线相切”的尺规作图过程．
已知：直线 $\text{[math]}$ 及直线 $\text{[math]}$ 外一点P（如图1）．

求作：⊙P ，使它与直线 $\text{[math]}$ 相切．

作法：如图2，

①在直线 $\text{[math]}$ 上任取两点A ， B；

②分别以点A ，点B为圆心，AP ， BP的长为半径画弧，两弧交于点Q；

③作直线PQ ，交直线 $\text{[math]}$ 于点C；

④以点P为圆心，PC的长为半径画⊙P ．

所以⊙P即为所求．

根据小融设计的尺规作图过程，

（1）使用直尺和圆规，依作法补全图形（保留作图痕迹）；

（2）完成下面的证明．
证明：连接AP ， AQ ， BP ， BQ ．

∵AP＝▲，BP＝▲，

∴点A ，点B在线段PQ的垂直平分线上．

∴直线AB是线段PQ的垂直平分线．

∵PQ⊥ $\text{[math]}$ ，PC是⊙P的半径，

∴⊙P与直线 $\text{[math]}$ 相切（）（填推理的依据）．

查看解析收藏纠错

+选题
22. 如图，在△ABC中，∠BAC＝90°，AD是BC边上的中线，AE∥BC ， CE∥AD ．

（1）求证：四边形ADCE是菱形；

（2）连接BE ，若∠ABC＝30°，AC＝2，求BE的长．

查看解析收藏纠错

+选题
23. 在平面直角坐标系 $\text{[math]}$ 中，直线 $\text{[math]}$ 与反比例函数 $\text{[math]}$ 的图象交于点 $\text{[math]}$ ， $\text{[math]}$ 两点．

（1）求 $\text{[math]}$ 的值；

（2）已知点 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 轴的垂线，分别交直线 $\text{[math]}$ 和反比例函数 $\text{[math]}$ 的图象于点 $\text{[math]}$ ，若线段 $\text{[math]}$ 的长随 $\text{[math]}$ 的增大而增大，直接写出 $\text{[math]}$ 的取值范围．

查看解析收藏纠错

+选题
24. 如图，⊙O是△ABC的外接圆，AB是直径，D是AC中点，过点A作⊙O的切线交直线OD于点P ，连接PC ．

（1）求证：∠PCA＝∠ABC；

（2）若BC＝4，tan∠APO＝ $\text{[math]}$ ，求PA的长．

查看解析收藏纠错

+选题

25. 2021年7月1日是中国共产党成立100周年纪念日．为了让全校学生牢固树立爱国爱党的崇高信念，某校开展了形式多样的党史学习教育活动．八、九年级各300名学生举行了一次党史知识竞赛后随机抽取了八、九年级各20名学生的成绩进行了整理与分析，部分信息如下：

a ．抽取九年级20名学生的成绩如下：

86	88	97	91	94	62	51	94	87	71
94	78	92	55	97	92	94	94	85	98

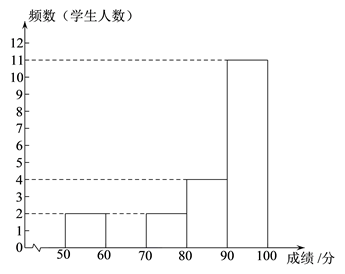
b ．抽取九年级20名学生的成绩频数分布直方图如下（数据分成5组： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）：

c ．九年级抽取的20名学生成绩的平均数、中位数、方差如下表：

年级	平均数	中位数	方差
九年级	85	m	192

请根据以上信息，回答下列问题：

（1）补全频数分布直方图，写出表中m的值；

（2）若90分及以上为优秀，估计此次知识竞赛中九年级成绩优秀的学生人数；

（3）通过分析随机抽取的八年级20名学生的成绩发现：这20名学生成绩的中位数为88，方差为80.4，且八、九两个年级随机抽取的共40名学生成绩的平均数是85.2

①求八年级这20名学生成绩的平均数；

②你认为哪个年级的成绩较好，说明理由（至少从两个不同的角度说明推断的合理性）．

查看解析收藏纠错

+选题

26. 在平面直角坐标系 $\text{[math]}$ 中，抛物线 $\text{[math]}$ 的对称轴是直线 $\text{[math]}$ ．

（1）用含 $\text{[math]}$ 的式子表示 $\text{[math]}$ ；

（2）求抛物线的顶点坐标；

（3）若抛物线与 $\text{[math]}$ 轴的一个交点为 $\text{[math]}$ ，且当 $\text{[math]}$ 时， $\text{[math]}$ 的取值范围是 $\text{[math]}$ ，结合函数图象，直接写出一个满足条件的 $\text{[math]}$ 的值和对应 $\text{[math]}$ 的取值范围．

查看解析收藏纠错

+选题
27. 已知∠MON＝90°，点A ， B分别在射线OM ， ON上（不与点O重合），且OA＞OB ， OP平分∠MON ，线段AB的垂直平分线分别与OP ， AB ， OM交于点C ， D ， E ，连接CB ，在射线ON上取点F ，使得OF＝OA ，连接CF ．

（1）依题意补全图形；

（2）求证：CB＝CF；

（3）用等式表示线段CF与AB之间的数量关系，并证明．

查看解析收藏纠错

+选题
28. 对于平面内点P和⊙G ，给出如下定义：T是⊙G上任意一点，点P绕点T旋转180°后得到点P＇，则称点P＇为点P关于⊙G的旋转点．下图为点P及其关于⊙G的旋转点P＇的示意图．在平面直角坐标系xOy中，⊙O的半径为1，点P（0，－2）．

（1）在点A（－1，0），B（0，4），C（2，2）中，是点P关于⊙O的旋转点的是；

（2）若在直线 $\text{[math]}$ 上存在点P关于⊙O的旋转点，求 $\text{[math]}$ 的取值范围；

（3）若点D在⊙O上，⊙D的半径为1，点P关于⊙D的旋转点为点P＇，请直接写出点P＇的横坐标 $\text{[math]}$ _P_＇的取值范围．

查看解析收藏纠错

+选题

北京市丰台区2021年中考数学二模试卷

一、单选题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨