河南省郑州市高新区2020届九年级上学期数学期中考试试卷

修改时间：2024-07-13 浏览次数：246 类型：期中考试编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、选择题

1. 两个人的影子在两个相反的方向，这说明（　　）

A . 他们站在阳光下 B . 他们站在路灯下 C . 他们站在路灯的两侧 D . 他们站在月光下

查看解析收藏纠错

+选题
2. 已知三条线段的长分别为1.5，2，3，则下列线段中，不能与它们组成比例线段的是（）

A . l B . 2.25 C . 4 D . 2

查看解析收藏纠错

+选题
3. 在一个不透明的布袋中装有40个黄、白两种颜色的球，除颜色外其他都相同，小红通过多次摸球试验后发现，摸到黄球的频率稳定在0.30左右，则布袋中黄球可能有（）

A . 12个 B . 14个 C . 18个 D . 28个

查看解析收藏纠错

+选题
4. 如图，王华用橡皮泥做了个圆柱，再用手工刀切去一部分，则其左视图是（）

A . B . C . D .

查看解析收藏纠错

+选题
5. 若 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
6. 已知点 $\text{[math]}$ 把线段 $\text{[math]}$ 分成两条线段 $\text{[math]}$ 、 $\text{[math]}$ ，且 $\text{[math]}$ ，下列说法错误的是（）

A . 如果 $\text{[math]}$ ，那么线段 $\text{[math]}$ 被点 $\text{[math]}$ 黄金分割 B . 如果 $\text{[math]}$ ，那么线段 $\text{[math]}$ 被点 $\text{[math]}$ 黄金分割 C . 如果线段 $\text{[math]}$ 被点 $\text{[math]}$ 黄金分割，那么 $\text{[math]}$ 与 $\text{[math]}$ 的比叫做黄金比 D . $\text{[math]}$ 是黄金比的近似值

查看解析收藏纠错

+选题
7. 已知关于x的方程x²+3x+a=0有一个根为﹣2，则另一个根为（　　）

A . 5 B . ﹣1 C . 2 D . ﹣5

查看解析收藏纠错

+选题
8. 如图，已知AB∥CD∥EF，它们依次交直线l₁、l₂于点A、D、F和点B、C、E，如果AD：DF＝3：1，BE＝10，那么CE等于（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
9. 如图，在△ABC中，∠ACB＝90°，分别以点A、C为圆心，以大于 $\text{[math]}$ AC的长为半径画弧，两弧相交于点D和E，作直线DE交AB于点F，交AC于点G，连接CF，以点C为圆心，以CF的长为半径画弧，交AC于点H.若∠A＝30°，BC＝2，则AH的长是（）

A . $\text{[math]}$ B . 2 C . $\text{[math]}$ +1 D . 2 $\text{[math]}$ ﹣2

查看解析收藏纠错

+选题
10. 如图，已知矩形 $\text{[math]}$ 中，点 $\text{[math]}$ 是边 $\text{[math]}$ 上的任一点，连接 $\text{[math]}$ ，过 $\text{[math]}$ 作 $\text{[math]}$ 的垂线交 $\text{[math]}$ 延长线于点 $\text{[math]}$ ，交边 $\text{[math]}$ 于点 $\text{[math]}$ ，则图中共有相似三角形（）

A . 6对 B . 5对 C . 4对 D . 3对

查看解析收藏纠错

+选题
11. 如图，在矩形ABCD中，M是BC边上一点，连接AM， $\text{[math]}$ 过点D作 $\text{[math]}$ ，垂足为 $\text{[math]}$ 若 $\text{[math]}$ ， $\text{[math]}$ ，则BM的长为 $\text{[math]}$ $\text{[math]}$

A . 1 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
12. 如图，四边形 $\text{[math]}$ 是边长为6的正方形，点 $\text{[math]}$ 在边 $\text{[math]}$ 上， $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ ，分别交 $\text{[math]}$ 于 $\text{[math]}$ 两点.若 $\text{[math]}$ 分别是 $\text{[math]}$ 的中点，则 $\text{[math]}$ 的长为（）

A . 3 B . $\text{[math]}$ C . $\text{[math]}$ D . 4

查看解析收藏纠错

+选题

二、填空题

13. 已知： $\text{[math]}$ 是反比例函数，则m=．

查看解析收藏纠错

+选题
14. 若菱形的两条对角线长分别是方程 $\text{[math]}$ 的两实根，则菱形的面积为.

查看解析收藏纠错

+选题
15. 关于x的一元二次方程 $\text{[math]}$ 有实数根，则实数a满足的条件是.

查看解析收藏纠错

+选题
16. 如图，在△ABC中，DE∥BC，BF平分∠ABC，交DE的延长线于点F，若AD=1，BD=2，BC=4，则EF=.

查看解析收藏纠错

+选题
17. 如图，平面直角坐标系 $\text{[math]}$ 中，已知 $\text{[math]}$ 和B点 $\text{[math]}$ ，点C是 $\text{[math]}$ 的中点，点P在x轴上，若以P、A、C为顶点的三角形与 $\text{[math]}$ 相似，那么点P的坐标是.

查看解析收藏纠错

+选题
18. 如图，在矩形ABCD中，AB=8，AD=6，点E为AB上一点，AE=2 $\text{[math]}$ ，点F在AD上，将△AEF沿EF折叠，当折叠后点A的对应点A′恰好落在BC的垂直平分线上时，折痕EF的长为.

查看解析收藏纠错

+选题

三、解答题

19. 校园安全受到全社会的广泛关注，某市某中学对部分学生就校园安全知识的了解程度，采用随机抽样调查的方式，并根据收集到的信息进行统计，绘制了尚不完整的统计图.请你根据统计图中所提供的信息解答下列问题：

（1）在这次活动中抽查了多少名中学生？

（2）若该中学共有学生1600人，请根据上述调查结果，估计该中学学生中对校园安全知识达到“了解”程度的人数.

（3）若从对校园安全知识达到“了解程度的2个女生和2个男生中随机抽取2人参加校园安全知识竞赛，请用树状图或列表法求出恰好抽到1个男生和1个女生的概率.

查看解析收藏纠错

+选题
20. 如图，已知点 $\text{[math]}$ 是坐标原点， $\text{[math]}$ 两点的坐标分别为 $\text{[math]}$ ， $\text{[math]}$ .

（1）以 $\text{[math]}$ 点为位似中心在 $\text{[math]}$ 轴的左侧将 $\text{[math]}$ 放大到原图的2倍（即新图与原图的相似比为2），画出对应的 $\text{[math]}$ ；

（2）若 $\text{[math]}$ 内部一点 $\text{[math]}$ 的坐标为 $\text{[math]}$ ，则点 $\text{[math]}$ 对应点 $\text{[math]}$ 的坐标是；

（3）求出变化后 $\text{[math]}$ 的面积 .

查看解析收藏纠错

+选题
21. 已知关于 $\text{[math]}$ 的一元二次方程 $\text{[math]}$ .
求证：

（1）方程总有两个不相等的实数根.

（2）若等腰 $\text{[math]}$ 的两边 $\text{[math]}$ 的长是这个方程的两个实数根，第三边 $\text{[math]}$ 的长为5. 求 $\text{[math]}$ 的周长.

查看解析收藏纠错

+选题
22. 《铁血红安》在中央一台热播后，吸引了众多游客前往影视基地游玩. 某天小明站在地面上给站在城楼上的小亮照相时发现：他的眼睛、凉亭顶端、小亮头顶三点恰好在一条直线上（如图）. 已知小明的眼睛离地面1. 65米，凉亭顶端离地面2米，小明到凉亭的距离为2米，凉亭离城楼底部的距离为40米，小亮身高1. 7米. 请根据以上数据求出城楼的高度.
.

查看解析收藏纠错

+选题
23. 某汽车租赁公司共有汽车50辆，市场调查表明，当租金为每辆每日200元时可全部租出，当租金每提高10元，租出去的车就减少2辆.

（1）当租金提高多少元时，公司的每日收益可达到10120元？

（2）汽车日常维护要一定费用，已知外租车辆每日维护费为100元，未租出的车辆维护费为50元，当租金为多少元时，公司的利润恰好为5500元？（利润=收益-维护费）

查看解析收藏纠错

+选题
24. 已知：如图，在平行四边形 $\text{[math]}$ 中，G、H分别是 $\text{[math]}$ 、 $\text{[math]}$ 的中点，E、O、F分别是对角线 $\text{[math]}$ 上的四等分点，顺次连接G、E、H、F.

（1）求证：四边形 $\text{[math]}$ 是平行四边形；

（2）当平行四边形 $\text{[math]}$ 满足条件时，四边形 $\text{[math]}$ 是菱形；

（3）若 $\text{[math]}$ ，探究四边形 $\text{[math]}$ 的形状，并说明理由.

查看解析收藏纠错

+选题
25. 如图

（1）问题发现
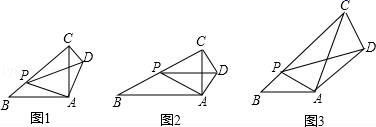
如图1，在Rt△ABC中，∠A=90°， $\text{[math]}$ =1，点P是边BC上一动点（不与点B重合），∠PAD=90°，∠APD=∠B，连接 CD.

①求 $\text{[math]}$ 的值；②求∠ACD的度数.

（2）拓展探究
如图 2，在Rt△ABC中，∠A=90°， $\text{[math]}$ =k.点P是边BC上一动点（不与点B重合），∠PAD=90°，∠APD=∠B，连接CD，请判断∠ACD与∠B 的数量关系以及PB与CD之间的数量关系，并说明理由.

（3）解决问题
如图 3，在△ABC中，∠B=45°，AB=4 $\text{[math]}$ ，BC=12，P 是边BC上一动点（不与点B重合），∠PAD=∠BAC，∠APD=∠B，连接CD.若 PA=5，请直接写出CD的长.

查看解析收藏纠错

+选题

河南省郑州市高新区2020届九年级上学期数学期中考试试卷

一、选择题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨