修改时间:2024-07-13 浏览次数:362 类型:中考模拟
| 套餐类型 | 月费(元/月) | 套餐内包含内容 | 套餐外资费 | ||
| 国内数据流量(GB) | 国内主叫(分钟) | 国内流量 | 国内主叫 | ||
| 套餐1 | 128 | 30 | 200 | 每5元1GB,用满3GB后每3元1GB,不足部分按照0.03/元MB收取 | 0.19元/分钟 |
| 套餐2 | 158 | 40 | 300 | ||
| 套餐3 | 198 | 60 | 500 | ||
| 套餐4 | 238 | 80 | 600 | ||
小武每月大约使用国内数据流量49GB,国内主叫350分钟,若想使每月付费最少,则他应预定的套餐是( )

a.各省区市 数据的频数分布直方图,如图1(数据分成6组,各组是
,
,
,
,
,
):
b.2020年第一季度 数据在这一组的是:4.6 4.9 5.0 5.1 5.3 5.4 6.3 7.4 7.5 7.8 7.8
c.30个省区市2020年第一季度及2019年 增速排名统计图,如图2:
d.北京2020年第一季度 数据约为7.5千亿,
增速排名为第22.

根据以上信息,回答下列问题:
①与2019年 增速排名相比,在疫情冲击下,2020年全国第一季度增速排名,部分省市有较大下滑,如D代表的湖北排名下滑最多.
②A、B、C分别代表的新疆、广西、青海位于西部地区,多为人口净流出或少量净流入,经济发展主要依靠本地劳动力供给,疫后复工复产效率相对较高,相对于2019年 增速排名位置靠前.

小华同学根据学习函数的经验,分别对函数 ,随自变量x的变化而变化的规律进行了探究.
下面是该同学的探究过程,请补充完整:
| | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| | 4.47 | 5.24 | 5.86 | 5.96 | 4.72 | 4.00 | |
| | 6.00 | 5.86 | 5.23 | 3.98 | 2.46 | 1.06 | 0 |
请你补全表格的相关数值,保留两位小数.


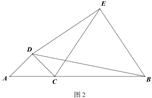
①求证: ;
②判断线段 与
的数量关系,并证明;
对于以上问题,小牧同学通过观察、实验,形成了解决该问题的几种思路:
想法1:尝试将点D为旋转中心,过点D作线段 垂线,交
延长线于点G , 连接
;通过证明
解决以上问题;
想法2:尝试将点D为旋转中心,过点D作线段 垂线,垂足为点G , 连接
.通过证明
解决以上问题;
想法3:尝试利用四点共圆,过点D作 垂线段
,连接
,通过证明D、F、B、E四点共圆,利用圆的相关知识解决以上问题.
请你参考上面的想法,证明 (一种方法即可).
试题篮