湖南省株洲市石峰区2019年中考数学模拟试卷（二)

1. ﹣ $\text{[math]}$ 的绝对值是（　　）

A . $\text{[math]}$ B . ﹣ $\text{[math]}$ C . 2 D . ﹣2

查看解析收藏纠错

+选题
2. 下列计算正确的是（）

A . a⁴+a³＝a⁷ B . a⁴•a³＝a¹² C . （a⁴）³＝a⁷ D . a⁴÷a³＝a

查看解析收藏纠错

+选题
3. 生物学家发现了某种花粉的直径约为0.0000036毫米，数据0.0000036用科学记数法表示正确的是（）

A . 3.6×10^﹣5 B . 0.36×10^﹣5 C . 3.6×10^﹣6 D . 0.36×10^﹣6

查看解析收藏纠错

+选题
4. 数据1，2，3，4，4，5的众数和中位数的差是（）

A . 1 B . ﹣0.5 C . 0.5 D . ﹣1

查看解析收藏纠错

+选题
5. 下列图形中，既是轴对称又是中心对称图形的是（）

A . B . C . D .

查看解析收藏纠错

+选题
6. 不等式组 $\text{[math]}$ 的解集为（）

A . x＞0 B . x＞1 C . 无解 D . 0＜x＜1

查看解析收藏纠错

+选题
7. 如图，在▱ABCD中，对角线AC与BD相交于点O，E是边CD的中点，连结 $\text{[math]}$ 若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的度数为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
8. 当x＞0时，y随x的增大而增大的函数是（）

A . y＝﹣x B . y＝ $\text{[math]}$ C . y＝－ $\text{[math]}$ D . y＝﹣x²

查看解析收藏纠错

+选题
9. 如图，已知点E是矩形ABCD的对角线AC上的一动点，正方形EFGH的顶点G、H都在边AD上，若AB=3，BC=4，则tan∠AFE的值（）

A . 等于 $\text{[math]}$ B . 等于 $\text{[math]}$ C . 等于 $\text{[math]}$ D . 随点E位置的变化而变化

查看解析收藏纠错

+选题
10. 如图，抛物线 $\text{[math]}$ 与 $\text{[math]}$ 轴交于点A（-1，0），顶点坐标（1，n）与 $\text{[math]}$ 轴的交点在（0，2），（0，3）之间（包含端点），则下列结论：① $\text{[math]}$ ；② $\text{[math]}$ ；③对于任意实数m，a+b≥am²+bm总成立；④关于 $\text{[math]}$ 的方程 $\text{[math]}$ 有两个不相等的实数根.其中结论正确的个数为 $\text{[math]}$ 　　 $\text{[math]}$

A . 1 个 B . 2 个 C . 3 个 D . 4 个

查看解析收藏纠错

+选题

11. 分式方程 $\text{[math]}$ 的解是．

查看解析收藏纠错

+选题
12. 已知a∥b ，某学生将一直角三角板放置如图所示，如果∠1＝35°，则∠2的度数为．

查看解析收藏纠错

+选题
13. 因式分解：x³﹣4x²+4x＝．

查看解析收藏纠错

+选题
14. 一个三角形的两边长分别为3和6，第三边长是方程x²-10x+21=0的根，则三角形的周长为.

查看解析收藏纠错

+选题
15. 我国古代数学著作《九章算术》中有一道阐述“盈不足术”的问题，译文为：“现有几个人共同购买一个物品，每人出8元，则多3元；每人出7元，则差4元．问这个物品的价格是多少元？”该物品的价格是元．

查看解析收藏纠错

+选题
16. 如图，正六边形ABCDEF外接圆的半径为4，则其内切圆的半径是．

查看解析收藏纠错

+选题
17. 如图，平行于x轴的直线与函数y＝ $\text{[math]}$ （k₁＞0，x＞0），y＝ $\text{[math]}$ （k₂＞0，x＞0）的图象分别相交于A ， B两点，点A在点B的右侧，C为x轴上的一个动点，若△ABC的面积为3，则k₁﹣k₂的值为．

查看解析收藏纠错

+选题
18. 如图，往竖直放置的在A处山短软管连接的粗细均匀细管组成的“U形装置中注入一定量的水，水面高度为9cm ，现将右边细管绕A处顺时针方向旋转60°到AB位置，则AB中水柱的长度为cm ．

查看解析收藏纠错

+选题

19. 计算： $\text{[math]}$

查看解析收藏纠错

+选题
20. 先化简，再求值：（x﹣1+ $\text{[math]}$ ）÷ $\text{[math]}$ ，其中x的值从不等式﹣1≤x＜2.5的整数解中选取．

查看解析收藏纠错

+选题
21. “高低杠”是女子体操特有的一个竞技项目，其比赛器材由高、低两根平行杠及若干支架组成，运动员可根据自己的身高和习惯在规定范围内调节高、低两杠间的距离．某兴趣小组根据高低杠器材的一种截面图编制了如下数学问题，请你解答．
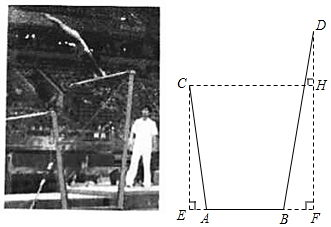
如图所示，底座上A，B两点间的距离为90cm．低杠上点C到直线AB的距离CE的长为155cm，高杠上点D到直线AB的距离DF的长为234cm，已知低杠的支架AC与直线AB的夹角∠CAE为82.4°，高杠的支架BD与直线AB的夹角∠DBF为80.3°．求高、低杠间的水平距离CH的长．（结果精确到1cm，参考数据sin82.4°≈0.991，cos82.4°≈0.132，tan82.4°≈7.500，sin80.3°≈0.983，cos80.3°≈0.168，tan80.3°≈5.850）

查看解析收藏纠错

+选题
22. 央视“经典咏流传”开播以来受到社会广泛关注.我市某校就“中华文化我传承——地方戏曲进校园”的喜爱情况进行了随机调查，对收集的信息进行统计，绘制了下面两副尚不完整的统计图.请你根据统计图所提供的信息解答下列问题：
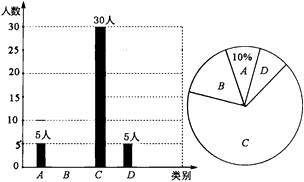
图中A表示“很喜欢”，B表示“喜欢”，C表示“一般”，D表示“不喜欢”.

（1）被调查的总人数是人，扇形统计图中C部分所对应的扇形圆心角的度数为.

（2）补全条形统计图；

（3）若该校共有学生1800人，请根据上述调查结果，估计该校学生中A类有人；

（4）在抽取的A类5人中，刚好有3个女生2个男生，从中随机抽取两个同学担任两角色，用树形图或列表法求出被抽到的两个学生性别相同的概率.

查看解析收藏纠错

+选题
23. 如图，四边形ABCD是矩形，E是BD上的一点，∠BAE＝∠BCE，∠AED＝∠CED，点G是BC，AE延长线的交点，AG与CD相交于点F．

（1）求证：四边形ABCD是正方形；

（2）当AE＝3EF，DF＝1时，求GF的值．

查看解析收藏纠错

+选题
24. 如图，一次函数y₁＝kx+b（k ， b为常数，k≠0）的图象与反比例函数y₂＝ $\text{[math]}$ （m为常数，m≠0）的图象相交于点M（1，4）和点N（4，n）．

（1）反比例函数与一次函数的解析式．

（2）函数y₂＝ $\text{[math]}$ 的图象（x＞0）上有一个动点C ，若先将直线MN平移使它过点C ，再绕点C旋转得到直线PQ ， PQ交x轴于点A ，交y轴点B ，若BC＝2CA ，求OA•OB的值．

查看解析收藏纠错

+选题
25. 如图，已知AB是⊙O的直径，AC是弦（不是直径），OD⊥AC垂足为G交⊙O于D ， E为⊙O上一点（异于A、B），连接ED交AC于点F ，过点E的直线交BA、CA的延长线分别于点P、M ，且ME＝MF ．

（1）求证：PE是⊙O的切线．

（2）若DF＝2，EF＝8，求AD的长．

（3）若PE＝6 $\text{[math]}$ ，sin∠P＝ $\text{[math]}$ ，求AE的长．

查看解析收藏纠错

+选题
26. 已知二次函数y＝x²+bx+c+1的图象与x轴交于点A（x₁ ， 0）、B（x₂ ， 0），且x₁＜x₂ ，与y轴的负半轴交于点C ．

（1）当b＝1时，求c的取值范围；

（2）如果以AB为直径的半圆恰好过点C ，求c的值；

（3）在（2）的条件下，如果二次函数的对称轴l与x轴、直线BC、直线AC的延长线分别交于点D、E、F ，且满足DE＝2EF ，求二次函数的表达式．

查看解析收藏纠错

+选题

湖南省株洲市石峰区2019年中考数学模拟试卷（二)

一、选择题

二、填空题

三、综合题

相关试卷收起∨

湖南省株洲市石峰区2019年中考数学模拟试卷（二)

一、选择题

二、填空题

三、综合题

相关试卷 收起∨

相关试卷收起∨