修改时间:2024-07-13 浏览次数:539 类型:中考模拟
请根据图表中数据填空:
①表中m的值为;
② B类部分的圆心角度数为°;
③估计C、D类学生大约一共有名.

九年级学生数学成绩频数分布表
成绩(单位:分) | 频数 | 频率 |
A类(80~100) | 24 | |
B类(60~79) | 12 | |
C类(40~59) | 8 | m |
D类(0~39) | 4 | |
学校 | 平均数(分) | 方差 | A、B类的频率和 |
城南中学 | 71 | 358 | 0.75 |
城北中学 | 71 | 588 | 0.82 |
请你评价这两所学校学生数学学业水平测试的成绩,提出一个解释来支持你的观点.
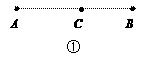
①写出小明妈妈在骑车由C处返回到A处的过程中,y与x的函数表达式及x的取值范围;

②在图③中画出整个过程中y与x的函数图象.(要求标出关键点的坐标)

试题篮