题型:综合题 题类:常考题 难易度:困难
江苏省盐城市东台市第四联盟2020届九年级上学期数学期中考试试卷
小军的证明思路是:如图(2),连接AP,由△ABP与△ACP面积之和等于△ABC的面积可以证得:PD+PE=CF.
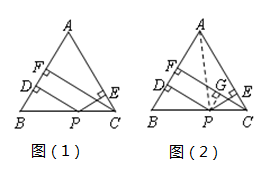
老师表扬了小军,并且告诉小军和小俊:在求解平面几何问题的时候,根据有关几何量与涉及的有关图形面积之间的内在联系,用面积或面积之间的关系表示有关线段间的关系,从而把要论证的线段之间的关系转化为面积的关系,并通过图形面积的等积变换对所论问题来进行求解的方法,这种方法称为“面积法”.
请你使用“面积法”解决下列问题:
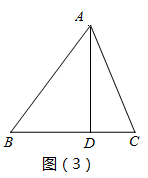
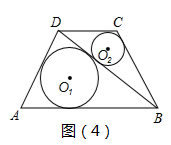
试题篮