2016年湖北省随州市中考数学试卷

1. ﹣ $\text{[math]}$ 的相反数是（　　）

A . ﹣ $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . ﹣ $\text{[math]}$

查看解析收藏纠错

+选题
2. 随着我国经济快速发展，轿车进入百姓家庭，小明同学在街头观察出下列四种汽车标志，其中既是中心对称图形，又是轴对称图形的是（　　）

A . B . C . D .

查看解析收藏纠错

+选题
3. 下列运算正确的是（　　）

A . a²•a³=a⁶ B . a⁵÷a²=a³ C . （﹣3a）³=﹣9a³ D . 2x²+3x²=5x⁴

查看解析收藏纠错

+选题
4. 如图，直线a∥b，直线c分别与a、b相交于A、B两点，AC⊥AB于点A，交直线b于点C．已知∠1=42°，则∠2的度数是（　　）

A . 38° B . 42° C . 48° D . 58°

查看解析收藏纠错

+选题
5. 不等式组 $\text{[math]}$ 的解集表示在数轴上，正确的是（　　）

A . B . C . D .

查看解析收藏纠错

+选题
6. 为了响应学校“书香校园”建设，阳光班的同学们积极捐书，其中宏志学习小组的同学捐书册数分别是：5，7，x，3，4，6．已知他们平均每人捐5本，则这组数据的众数、中位数和方差分别是（　　）

A . 5，5， $\text{[math]}$ B . 5，5，10 C . 6，5.5， $\text{[math]}$ D . 5，5， $\text{[math]}$

查看解析收藏纠错

+选题
7. 如图，D、E分别是△ABC的边AB、BC上的点，且DE∥AC，AE、CD相交于点O，若S_△_DOE：S_△_COA=1：25，则S_△_BDE与S_△_CDE的比是（　　）

A . 1：3 B . 1：4 C . 1：5 D . 1：25

查看解析收藏纠错

+选题
8. 随州市尚市“桃花节”观赏人数逐年增加，据有关部门统计，2014年约为20万人次，2016年约为28.8万人次，设观赏人数年均增长率为x，则下列方程中正确的是（　　）

A . 20（1+2x）=28.8 B . 28.8（1+x）²=20 C . 20（1+x）²=28.8 D . 20+20（1+x）+20（1+x）²=28.8

查看解析收藏纠错

+选题
9. 如图是某工件的三视图，则此工件的表面积为（　　）

A . 15πcm² B . 51πcm² C . 66πcm² D . 24πcm²

查看解析收藏纠错

+选题
10. 二次函数y=ax²+bx+c（a≠0）的部分图象如图所示，图象过点（﹣1，0），对称轴为直线x=2，下列结论：（1）4a+b=0；（2）9a+c＞3b；（3）8a+7b+2c＞0；（4）若点A（﹣3，y₁）、点B（﹣ $\text{[math]}$ ，y₂）、点C（ $\text{[math]}$ ，y₃）在该函数图象上，则y₁＜y₃＜y₂；（5）若方程a（x+1）（x﹣5）=﹣3的两根为x₁和x₂ ，且x₁＜x₂ ，则x₁＜﹣1＜5＜x₂ ．其中正确的结论有（　　）

A . 2个 B . 3个 C . 4个 D . 5个

查看解析收藏纠错

+选题

11. 2015年“圣地车都”﹣﹣随州改装车的总产值为14.966亿元，其中14.966亿元用科学记数法表示为元．

查看解析收藏纠错

+选题
12. 已知等腰三角形的一边长为9，另一边长为方程x²﹣8x+15=0的根，则该等腰三角形的周长为．

查看解析收藏纠错

+选题
13. 如图，在△ABC中，∠ACB=90°，M、N分别是AB、AC的中点，延长BC至点D，使CD= $\text{[math]}$ BD，连接DM、DN、MN．若AB=6，则DN=．

查看解析收藏纠错

+选题
14. 如图，直线y=x+4与双曲线y= $\text{[math]}$ （k≠0）相交于A（﹣1，a）、B两点，在y轴上找一点P，当PA+PB的值最小时，点P的坐标为．

查看解析收藏纠错

+选题
15. 如图（1），PT与⊙O₁相切于点T，PAB与⊙O₁相交于A、B两点，可证明△PTA∽△PBT，从而有PT²=PA•PB．请应用以上结论解决下列问题：如图（2），PAB、PCD分别与⊙O₂相交于A、B、C、D四点，已知PA=2，PB=7，PC=3，则CD=．

查看解析收藏纠错

+选题
16.
如图，边长为1的正方形ABCD的对角线AC、BD相交于点O．有直角∠MPN，使直角顶点P与点O重合，直角边PM、PN分别与OA、OB重合，然后逆时针旋转∠MPN，旋转角为θ（0°＜θ＜90°），PM、PN分别交AB、BC于E、F两点，连接EF交OB于点G，则下列结论中正确的是．
①EF= $\text{[math]}$ OE；②S_四边形_OEBF：S_正方形_ABCD=1：4；③BE+BF= $\text{[math]}$ OA；④在旋转过程中，当△BEF与△COF的面积之和最大时，AE= $\text{[math]}$ ；⑤OG•BD=AE²+CF² ．

查看解析收藏纠错

+选题

17. 计算：﹣|﹣1|+ $\text{[math]}$ •cos30°﹣（﹣ $\text{[math]}$ ）^﹣²+（π﹣3.14）⁰ ．

查看解析收藏纠错

+选题
18. 先化简，再求值：（ $\text{[math]}$ ﹣x+1）÷ $\text{[math]}$ ，其中x= $\text{[math]}$ ﹣2．

查看解析收藏纠错

+选题
19. 某校学生利用双休时间去距学校10km的炎帝故里参观，一部分学生骑自行车先走，过了20min后，其余学生乘汽车沿相同路线出发，结果他们同时到达．已知汽车的速度是骑车学生速度的2倍，求骑车学生的速度和汽车的速度．

查看解析收藏纠错

+选题
20. 国务院办公厅2015年3月16日发布了《中国足球改革的总体方案》，这是中国足球历史上的重大改革．为了进一步普及足球知识，传播足球文化，我市举行了“足球进校园”知识竞赛活动，为了解足球知识的普及情况，随机抽取了部分获奖情况进行整理，得到下列不完整的统计图表：
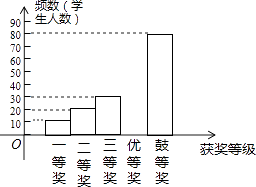
获奖等次
频数
频率
一等奖
10
0.05
二等奖
20
0.10
三等奖
30
b
优胜奖
a
0.30
鼓励奖
80
0.40
请根据所给信息，解答下列问题：

（1） a=，b=，且补全频数分布直方图；

（2）若用扇形统计图来描述获奖分布情况，问获得优胜奖对应的扇形圆心角的度数是多少？

（3）在这次竞赛中，甲、乙、丙、丁四位同学都获得一等奖，若从这四位同学中随机选取两位同学代表我市参加上一级竞赛，请用树状图或列表的方法，计算恰好选中甲、乙二人的概率．

查看解析收藏纠错

+选题
21. 某班数学兴趣小组利用数学活动课时间测量位于烈山山顶的炎帝雕像高度，已知烈山坡面与水平面的夹角为30°，山高857.5尺，组员从山脚D处沿山坡向着雕像方向前进1620尺到达E点，在点E处测得雕像顶端A的仰角为60°，求雕像AB的高度．

查看解析收藏纠错

+选题
22. 如图，AB是⊙O的弦，点C为半径OA的中点，过点C作CD⊥OA交弦AB于点E，连接BD，且DE=DB．

（1）判断BD与⊙O的位置关系，并说明理由；

（2）若CD=15，BE=10，tanA= $\text{[math]}$ ，求⊙O的直径．

查看解析收藏纠错

+选题
23. 九年级（3）班数学兴趣小组经过市场调查整理出某种商品在第x天（1≤x≤90，且x为整数）的售价与销售量的相关信息如下．已知商品的进价为30元/件，设该商品的售价为y（单位：元/件），每天的销售量为p（单位：件），每天的销售利润为w（单位：元）．
时间x（天）
1
30
60
90
每天销售量p（件）
198
140
80
20

（1）求出w与x的函数关系式；

（2）问销售该商品第几天时，当天的销售利润最大？并求出最大利润；

（3）该商品在销售过程中，共有多少天每天的销售利润不低于5600元？请直接写出结果．

查看解析收藏纠错

+选题
24.
爱好思考的小茜在探究两条直线的位置关系查阅资料时，发现了“中垂三角形”，即两条中线互相垂直的三角形称为“中垂三角形”．如图（1）、图（2）、图（3）中，AM、BN是△ABC的中线，AN⊥BN于点P，像△ABC这样的三角形均为“中垂三角形”．设BC=a，AC=b，AB=c．
【特例探究】

（1）如图1，当tan∠PAB=1，c=4 $\text{[math]}$ 时，a=，b=；
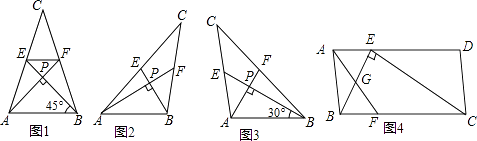
如图2，当∠PAB=30°，c=2时，a=，b=；

（2）【归纳证明】请你观察（1）中的计算结果，猜想a²、b²、c²三者之间的关系，用等式表示出来，并利用图3证明你的结论．

（3）【拓展证明】如图4，▱ABCD中，E、F分别是AD、BC的三等分点，且AD=3AE，BC=3BF，连接AF、BE、CE，且BE⊥CE于E，AF与BE相交点G，AD=3 $\text{[math]}$ ，AB=3，求AF的长．

查看解析收藏纠错

+选题
25.
已知抛物线y=a（x+3）（x﹣1）（a≠0），与x轴从左至右依次相交于A、B两点，与y轴相交于点C，经过点A的直线y=﹣ $\text{[math]}$ x+b与抛物线的另一个交点为D．

（1）若点D的横坐标为2，求抛物线的函数解析式；

（2）若在第三象限内的抛物线上有点P，使得以A、B、P为顶点的三角形与△ABC相似，求点P的坐标；

（3）在（1）的条件下，设点E是线段AD上的一点（不含端点），连接BE．一动点Q从点B出发，沿线段BE以每秒1个单位的速度运动到点E，再沿线段ED以每秒 $\text{[math]}$ 个单位的速度运动到点D后停止，问当点E的坐标是多少时，点Q在整个运动过程中所用时间最少？

查看解析收藏纠错

+选题

2016年湖北省随州市中考数学试卷

一、选择题

二、填空题（本大题共6个小题，每小题3分，共18分）

三、解答题（本题共9小题，共72分，解答应写出必要演算步骤，文字说明或证明过程）

相关试卷收起∨

获奖等次	频数	频率
一等奖	10	0.05
二等奖	20	0.10
三等奖	30	b
优胜奖	a	0.30
鼓励奖	80	0.40

时间x（天）	1	30	60	90
每天销售量p（件）	198	140	80	20

2016年湖北省随州市中考数学试卷

一、选择题

二、填空题（本大题共6个小题，每小题3分，共18分）

三、解答题（本题共9小题，共72分，解答应写出必要演算步骤，文字说明或证明过程）

相关试卷 收起∨

相关试卷收起∨