小题精练 07 圆周运动问题-备考2025年高考物理题型突破讲练

1. 如图所示，普通轮椅一般由轮椅架、车轮、刹车装置等组成。车轮有大车轮和小车轮，大车轮上固定有手轮圈，手轮圈由患者直接推动。已知大车轮、手轮圈、小车轮的半径之比为9∶8∶1，假设轮椅在地面上做直线运动，手和手轮圈之间、车轮和地面之间都不打滑，则下列说法正确的是（）

A . 大车轮与小车轮的角速度之比为9∶1 B . 手轮圈与小车轮的角速度之比为8∶9 C . 大车轮轴心与小车轮轴心的速度之比为1∶1 D . 大车轮与手轮圈两边缘的线速度之比为1∶1

查看解析收藏纠错

+选题
2. 如图所示，某款自行车大齿轮总齿数为 $\text{[math]}$ ，小齿轮总齿数为 $\text{[math]}$ ，后轮直径为D。某同学骑行时，匀速蹬脚踏板带动大齿轮每秒钟转N圈，则自行车向前行驶的车速为（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
3. 在东北严寒的冬天，有一项“泼水成冰”的游戏，具体操作是把一杯滚烫的开水按一定的弧线均匀快速地泼向空中，泼洒出的小水珠和热气被瞬间凝结成冰而形成壮观的场景。如图甲所示是某人玩泼水成冰游戏的精彩瞬间，图乙为其示意图。假设泼水过程中杯子做匀速圆周运动，在 $\text{[math]}$ 内杯子旋转了 $\text{[math]}$ 。下列说法正确的是（　　）

A . P位置的小水珠速度方向沿a方向 B . P、Q两位置，杯子的向心加速度相同 C . 杯子在旋转时的线速度大小约为 $\text{[math]}$ D . 杯子在旋转时的向心加速度大小约为 $\text{[math]}$

查看解析收藏纠错

+选题
4. 如图1所示为某修正带照片，图2为其结构示意图。修正带由出带轮、传动轮、收带轮、基带、出带口等组成。测量可知出带轮有45齿，半径为 $\text{[math]}$ ，传动轮齿数未知，半径为 $\text{[math]}$ ，收带轮有15齿，半径未知，下列选项正确的是（）

A . 使用时，出带轮与收带轮转动方向相反 B . 根据题中信息，可以算出传动轮的齿数 C . 根据题中信息，不能算出收带轮轴心到齿轮边缘的半径 D . 在纸面长时间匀速拉动修正带时，出带轮边缘某点的向心加速度大小不变

查看解析收藏纠错

+选题
5. 图（a）是某型号气门结构的简化图：金属块和固定弹簧座连接弹簧上端和下端，偏心轮轴位置固定，偏心轮以恒定角速度ω转动，带动金属块与推杆整体上下往复运动，配合气门机构完成进气、出气，此过程弹簧一直处于压缩状态，偏心轮与金属块始终保持接触。偏心轮横截面如图（b），在t=0时通过轮轴的偏心轮直径恰好处于水平位置，则（　　）

A . 推杆上下往复运动的周期为 $\text{[math]}$ B . $\text{[math]}$ 时弹簧的弹性势能最大 C . 偏心轮上各点的线速度最大值为 $\text{[math]}$ D . 偏心轮上各点的向心加速度最大值为 $\text{[math]}$

查看解析收藏纠错

+选题
6. 如图所示，直径为d的竖直圆筒绕中心轴线以恒定的转速匀速转动。一子弹以水平速度沿圆筒直径方向从左侧射入圆筒，从右侧射穿圆筒后发现两弹孔在同一竖直线上且相距为h，重力加速度为g，则（）

A . 子弹在圆筒中的水平速度为 $\text{[math]}$ B . 子弹在圆筒中的水平速度为 $\text{[math]}$ C . 圆筒转动的角速度可能为 $\text{[math]}$ D . 圆筒转动的角速度可能为 $\text{[math]}$

查看解析收藏纠错

+选题
7. 在我国汉代，劳动人民就已经发明了辘轳，如图所示，可转动的把手边缘上 $\text{[math]}$ 点到转轴的距离为 $\text{[math]}$ ，辘轳边缘 $\text{[math]}$ 点到转轴的距离为 $\text{[math]}$ ，忽略空气阻力。在水桶离开水面后加速往上运动的过程中，下列说法正确的有（　　）

A . 把手边缘上 $\text{[math]}$ 点的角速度等于辘轳边缘 $\text{[math]}$ 点的角速度 B . 水桶上升的速度大小等于把手边缘上 $\text{[math]}$ 点的线速度大小 C . 绳子拉力对水桶做的功等于水桶和水的机械能的增加量 D . 拉力对水桶的冲量等于水桶动量的变化量

查看解析收藏纠错

+选题

8. 如图所示，摩托车手在水平弯道上匀速转弯时（　　）

A . 车手身体各处的加速度大小都相等 B . 车和人的总重力与地面对车的支持力是一对平衡力 C . 车对地面的压力与地面对车的作用力是一对作用力与反作用力 D . 地面对车的作用力不大于车和人的总重力

查看解析收藏纠错

+选题
9. 为了使汽车快速安全通过弯道，高速公路转弯处的路面通常设计成外侧高、内侧低。已知某高速公路转弯处是一圆弧，圆弧半径r=850m，路面倾角θ=6°（tan6°=0.105），汽车与路面的摩擦因数μ=0.6，则在该弯道处（　　）

A . 汽车受到重力、支持力和向心力 B . 汽车所需的向心力等于其所受地面的支持力 C . 当汽车速度等于120km/h时，汽车会受到平行于路面指向弯道内侧的摩擦力 D . 若汽车速度小于60km/h，汽车会向内侧滑动

查看解析收藏纠错

+选题
10. 如图为某闯关游戏简化图。一绕过其圆心O的竖直轴顺时针匀速转动的圆形转盘浮在水面上，转盘表面始终保持水平，M为转盘边缘上一点。某时刻，一挑战者从水平跑道边缘 $\text{[math]}$ 点以速度 $\text{[math]}$ 向右跳出，初速度方向平行于 $\text{[math]}$ 方向，且运动轨迹与此时刻 $\text{[math]}$ 在同一竖直平面内，随后参赛者正好落在M点，不计空气阻力。下列说法正确的是（　　）

A . 若跳出时刻不变，仅增大 $\text{[math]}$ ，参赛者必定落水 B . 若跳出时刻不变，仅减小 $\text{[math]}$ ，参赛者一定会落在OM之间 C . 若跳出时刻不变，仅增大转盘的转速，参赛者不可能落在M点 D . 若跳出时刻不变，仅减小转盘的转速，参赛者可能落在M点

查看解析收藏纠错

+选题
11. 如图所示，水平轻弹簧一端连接物块m，另一端固定在水平转盘的中心轴上，转盘绕中心轴匀速转动的角速度为ω，弹簧没有超过弹性限度，转盘足够大。已知物块与转盘间的动摩擦因数为μ，弹簧原长为l₀ ，劲度系数为 $\text{[math]}$ ， g为重力加速度。以下说法正确的是（　　）

A . $\text{[math]}$ 时，弹簧弹力一定为0 B . $\text{[math]}$ 时，弹簧长度可能为 $\text{[math]}$ C . ω由0缓慢增大，摩擦力一直增大 D . ω由0缓慢增大，弹簧的弹力不为零，且一直增大

查看解析收藏纠错

+选题
12. 汽车的自动泊车系统持续发展，现有更先进的“全自动泊车”。如图所示为某次电动汽车自动泊车全景示意图。汽车按图示路线（ $\text{[math]}$ m圆弧与直线构成）顺利停车。汽车与地面间的动摩擦因数为0.3（最大静摩擦力等于滑动摩擦力），重力加速度g＝10m/s² ，汽车可视为质点，下列说法正确的是（　　）

A . 汽车在匀速转弯过程中做匀变速曲线运动 B . 匀速转弯时，汽车空载与满载的最大允许速度一样大 C . 汽车泊车过程中重力的冲量为零 D . 汽车在泊车过程中受到的摩擦力总是与运动方向相反

查看解析收藏纠错

+选题
13. 如图所示，光滑的圆锥体固定在水平地面上，其轴线沿竖直方向，在圆锥体顶用长 $\text{[math]}$ 的细线悬挂一质量 $\text{[math]}$ 的小球（可视为质点），小球静止时细线与圆锥表面平行且细线与轴线的夹角 $\text{[math]}$ 。已知圆锥体的高度 $\text{[math]}$ ，细线能承受的最大拉力 $\text{[math]}$ ，取重力加速度大小 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 。现使圆锥体绕其轴线缓慢加速转动，小球也随圆锥体一起做角速度缓慢增大的圆周运动（不同时间内均可视为匀速圆周运动）。

（1）求小球即将离开圆锥体表面时的角速度大小 $\text{[math]}$ ；

（2）当小球的角速度大小 $\text{[math]}$ 时，求细线上的拉力大小 $\text{[math]}$ ；

（3）若细线上的拉力达到最大拉力的瞬间细线绷断，此瞬间小球速度不受影响，求小球落到水平地面的位置到圆锥体轴线的距离d。

查看解析收藏纠错

+选题

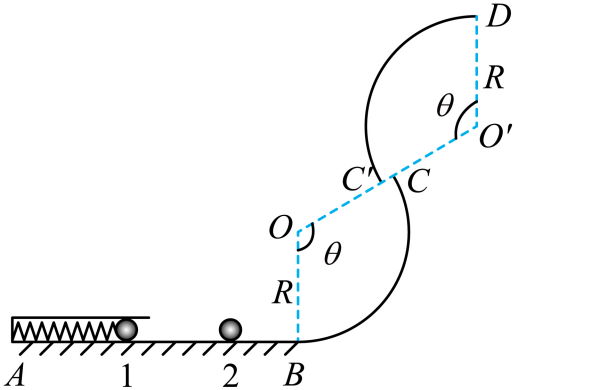
14. 如图所示为某弹射游戏装置，游戏轨道由水平直轨道AB和两个半径为 $\text{[math]}$ 、圆心角 $\text{[math]}$ 的圆弧轨道BC、 $\text{[math]}$ 组成，OB、 $\text{[math]}$ 竖直，小球（可视为质点）能无碰撞地从轨道BC进入轨道 $\text{[math]}$ 。小球1被固定于A处的弹簧弹出后，与静置在水平轨道的小球2发生弹性碰撞。游戏设置一、二、三等奖：若小球2能够进入圆弧轨道 $\text{[math]}$ 获三等奖，若小球2能在圆弧轨道 $\text{[math]}$ （不包括D点）段脱离获二等奖，若小球1能在圆弧轨道 $\text{[math]}$ （不包括D点）段脱离则获一等奖，其他情况都不能获奖。已知小球1的质量 $\text{[math]}$ ，小球2的质量 $\text{[math]}$ ，重力加速度g取 $\text{[math]}$ ，忽略一切摩擦，不考虑小球间的二次碰撞。

（1）若游戏能获奖，则小球2进入B点时，求轨道BC对小球弹力的最小值；

（2）小球2碰后的速度多大时，游戏能获二等奖；

（3）弹性势能满足什么条件时可获一等奖。

查看解析收藏纠错

+选题
15. 如图甲所示，筒车是利用水流带动车轮，使装在车轮上的竹筒自动将水提上岸进行灌溉。其简化模型如图乙所示，转轴为O，C、O、D在同一高度，A、B分别为最低点和最高点，E、F为水面。筒车在水流的推动下做匀速圆周运动，竹筒顺时针转动，其做匀速圆周运动的半径为R，角速度大小为 $\text{[math]}$ 。竹筒在A点开始打水，从F点离开水面。假设从A点到B点的过程中，竹筒所装的水质量为m且保持不变，重力加速度为g。下列说法正确的是（　　）

A . 竹筒做匀速圆周运动的周期为 $\text{[math]}$ B . 竹筒从C点到B点的过程中，重力的功率逐渐减小 C . 竹筒过C点时，竹筒对水的作用力大小为 $\text{[math]}$ D . 水轮车上装有16个竹筒，则相邻竹筒打水的时间间隔为 $\text{[math]}$

查看解析收藏纠错

+选题
16. 汽车行驶中经常会经过一些凹凸不平的路面，其凹凸部分路面可以看作圆弧的一部分，如图所示的A、B、C处，其中B处的曲率半径最大，A处的曲率半径为 $\text{[math]}$ ， C处的曲率半径为 $\text{[math]}$ ， $\text{[math]}$ ，重力加速度为 $\text{[math]}$ 。若有一辆可视为质点、质量为 $\text{[math]}$ 的小汽车与路面之间各处的动摩擦因数均为 $\text{[math]}$ ，当该车以恒定的速率 $\text{[math]}$ 沿这段凹凸路面行驶经过A、B、C三点时，下列说法正确的是（　　）

A . 汽车在A处受到的摩擦力大小为 $\text{[math]}$ B . 汽车经过A处时处于失重状态，经过C处时处于超重状态 C . 汽车在A点的行驶速度小于 $\text{[math]}$ 时，汽车将做平抛运动 D . 汽车经过C处时所受的向心力最小

查看解析收藏纠错

+选题
17. 如图所示，竖直平面内固定有一个半径为R的光滑圆环形细管，现给小球（直径略小于管内径）一个初速度，使小球在管内做圆周运动，小球通过最高点时的速度为v。已知重力加速度为g，则下列叙述中正确的是（　　）

A . v的最小值为 $\text{[math]}$ B . 当 $\text{[math]}$ 时，小球处于完全失重状态，不受力的作用 C . 当 $\text{[math]}$ 时，轨道对小球的弹力方向竖直向下 D . 当v由 $\text{[math]}$ 逐渐减小的过程中，轨道对小球的弹力也逐渐减小

查看解析收藏纠错

+选题
18. 人们用滑道从高处向低处运送货物．如图所示，可看作质点的货物从 $\text{[math]}$ 圆弧滑道顶端 $\text{[math]}$ 点静止释放，沿滑道运动到圆弧末端 $\text{[math]}$ 点时速度大小为 $\text{[math]}$ 。已知货物质量为 $\text{[math]}$ ，滑道高度 $\text{[math]}$ 为 $\text{[math]}$ ，且过 $\text{[math]}$ 点的切线水平，重力加速度取 $\text{[math]}$ 。关于货物从 $\text{[math]}$ 点运动到 $\text{[math]}$ 点的过程，下列说法正确的有（）

A . 重力做的功为 $\text{[math]}$ B . 克服阻力做的功为 $\text{[math]}$ C . 经过 $\text{[math]}$ 点时向心加速度大小为 $\text{[math]}$ D . 经过 $\text{[math]}$ 点时对轨道的压力大小为 $\text{[math]}$

查看解析收藏纠错

+选题
19. 如图所示，两个 $\text{[math]}$ 圆弧轨道固定在水平地面上，半径R相同，a轨道由金属凹槽制成，b轨道由金属圆管制成（圆管内径远小于半径R），均可视为光滑轨道，在两轨道右端的正上方分别将金属小球A和B（直径略小于圆管内径）由静止释放，小球距离地面的高度分别用 $\text{[math]}$ 和 $\text{[math]}$ 表示，下列说法中正确的是（）

A . 若 $\text{[math]}$ ，两小球都能沿轨道运动到最高点 B . 若 $\text{[math]}$ ，两小球在轨道上上升的最大高度均为 $\text{[math]}$ C . 适当调整 $\text{[math]}$ 和 $\text{[math]}$ ，均可使两小球从轨道最高点飞出后，恰好落在轨道右端口处 D . 若使小球沿轨道运动并且从最高点飞出， $\text{[math]}$ 的最小值为 $\text{[math]}$ ， B小球在 $\text{[math]}$ 的任何高度释放均可

查看解析收藏纠错

+选题
20. 如图所示，AB为竖直光滑圆弧的直径，其半径R=0.9m，A端沿水平方向。水平轨道BC与半径r=0.5m的光滑圆弧轨道CDE相接于C点，D为圆轨道的最低点，圆弧轨道CD、DE对应的圆心角θ=37°。圆弧和倾斜传送带EF相切于E点，EF的长度为l=10m。一质量为M=1kg的物块（视为质点）从水平轨道上某点以某一速度冲上竖直圆轨道，并从A点飞出，经过C点恰好沿切线进入圆弧轨道，再经过E点，随后滑上传送带EF。已知物块经过E点时速度大小与经过C点时速度大小相等，物块与传送带EF间的动摩擦因数μ=0.75，取g=10m/s² ， sin37°=0.6，cos37=0.8。求：

（1）物块从A点飞出的速度大小v_A和在A点受到的压力大小F_A；

（2）物块到达C点时的速度大小v_C及对C点的压力大小F_C；

（3）若传送带顺时针运转的速率为v=4m/s，求物块从E端到F端所用的时间。

查看解析收藏纠错

+选题

21. 如图所示，在水平桌面上有一轻质弹簧，弹簧左端固定，现有一质量为m的小球（可视为质点）将水平轻质弹簧压缩x₀长度后由静止释放，小球弹出后经A点水平抛出，恰好从B点沿B点切线方向进入半径为R的竖直圆管中（圆管内径略大于小球直径），小球从圆管最高点E离开后又恰能到达B点。已知E、O、C三点在同一竖直线上，∠BOC=60°，弹簧的弹性势能E_p与弹簧的形变量x以及弹簧的劲度系数k之间的关系式为 $\text{[math]}$ ，重力加速度为g，不计空气阻力和所有摩擦，则小球经弹簧弹出从A到达E又回到B的过程中，下列说法正确的是（　　）

A . 小球从圆管最高点E离开时受到圆管壁竖直向下的压力大小为 $\text{[math]}$ B . 小球从A点水平抛出的速度大小为 $\text{[math]}$ C . A、B两点之间的高度差为 $\text{[math]}$ D . 弹簧的劲度系数为 $\text{[math]}$

查看解析收藏纠错

+选题
22. 如图所示，长度为l的轻绳一端固定在O点，另一端系着一个质量为m的小球，当小球在最低点时，获得一个水平向右的初速度 $\text{[math]}$ ，重力加速度为g ，不计空气阻力。在此后的运动过程中，下列说法正确的是（　　）

A . 小球恰好能到达竖直面内的最高点 B . 当小球运动到最右端时，小球所受的合力大小为2mg C . 轻绳第一次刚好松弛时，轻绳与竖直方向夹角的余弦值为 $\text{[math]}$ D . 初状态在最低点时，细绳对小球的拉力大小为4mg

查看解析收藏纠错

+选题
23. 如图所示是杂技演员用细绳悬挂杯子在表演“水流星”的节目，对于杯子经过最高点时水的受力情况，下列说法正确的是（）

A . 水处于失重状态，不受重力的作用 B . 杂技运动员可通过技术调整使杯子在最高点的速度为零 C . 由于水做圆周运动，因此必然受到重力和向心力的作用 D . 杯底对水的作用力可能为零

查看解析收藏纠错

+选题
24. 如图所示，一半径为R、粗糙程度处处相同的半圆形轨道竖直固定放置，直径POQ水平。一质量为m的小球（可看成质点）从P点上方高为R处由静止开始下落，恰好从P点进入轨道。小球滑到轨道最低点N时，对轨道的压力大小为4mg，g为重力加速度。用W表示小球从P点运动到N点的过程中克服摩擦力所做的功，则（）

A . W＝ $\text{[math]}$ mgR，小球恰好可以到达Q点 B . W> $\text{[math]}$ mgR，小球不能到达Q点 C . W＝ $\text{[math]}$ mgR，小球到达Q点后，继续上升一段距离 D . W< $\text{[math]}$ mgR，小球到达Q点后，继续上升一段距离

查看解析收藏纠错

+选题
25. 如图所示，一个圆形的光滑绝缘空心管道固定在竖直面上。过管道的圆心 $\text{[math]}$ 点的水平直径上，在A点处固定一个电荷量大小为 $\text{[math]}$ 的正电荷，在B点固定一个未知电荷。在这两个点电荷共同产生的电场中，一个可以看作质点，质量为 $\text{[math]}$ ，电荷量大小未知的带电小球，在管道内进行圆周运动。当这个带电小球以特定的速度经过管道的最低点 $\text{[math]}$ 点时，小球恰好与空心管上、下壁均无挤压且无沿切线方向的加速度， $\text{[math]}$ 间的距离为L， $\text{[math]}$ ， $\text{[math]}$ ，静电力常量为 $\text{[math]}$ 。则以下说法正确的是（　　）

A . 小球带负电 B . $\text{[math]}$ 处点电荷为负电荷，电荷量大小为 $\text{[math]}$ C . 小球运动到最高点，空心管对小球的作用力大小为 $\text{[math]}$ ，方向竖直向上 D . 小球从最低点运动到最高点，电势能减小

查看解析收藏纠错

+选题
26. 某同学的寒假物理选做作业——原创题目荣获一等奖。题目如下：一个四分之三圆形轨道竖直固定于水平面上，一个小球（可视为质点）由四分之三圆形轨道左侧入口A正上方静止释放自由下落，已知小球与A点距离为h ，圆形轨道半径为R ，不计空气阻力，若小球在BC段上脱离轨道，下列说法正确的是（）

A . h的取值范围为 $\text{[math]}$ B . 脱离点与O点所在水平面之间的距离为 $\text{[math]}$ C . 当小球到达最高点时，小球与水平面之间的距离为 $\text{[math]}$ D . 若小球能经过O点，则 $\text{[math]}$

查看解析收藏纠错

+选题
27. 如图所示，半径 $\text{[math]}$ 的光滑圆弧轨道固定在竖直平面内，轨道的一个端点B和圆心O的连线与水平方向间的夹角θ=37°，另一端点C为轨道的最低点，其切线水平。一质量M=2kg、板长L=0.65m的滑板静止在光滑水平地面上，左端紧靠C点，其上表面所在平面与圆弧轨道C点和右侧固定平台D等高。质量为m=1kg的物块（可视为质点）从空中A点以v₀=0.6m/s的速度水平抛出，恰好从轨道的B端沿切线方向进入圆弧轨道，然后沿圆弧轨道滑下经C点滑上滑板。滑板运动到平台D时被牢固粘连。已知物块与滑板间的动摩擦因数μ=0.5，滑板右端到平台D左侧的距离s在（0.1m<s<0.5m范围内取值。取g=10m/s² ， sin37°=0.6，cos37°=0.8。求：

（1）物块到达B点时的速度大小v_B；

（2）物块经过C点时对圆弧轨道的压力大小；

（3）试讨论物块刚滑上平台D时的动能E_kD与s的大小关系。

查看解析收藏纠错

+选题

28. 如图所示，M、N两个钉子固定于相距a的两点，M的正上方有不可伸长的轻质细绳，一端固定在M上，另一端连接位于M正下方放置于水平地面质量为m的小木块B，绳长与M到地面的距离均为10a，质量为2m的小木块A，沿水平方向于B发生弹性碰撞，碰撞时间极短，A与地面间摩擦因数为 $\text{[math]}$ ，重力加速为g，忽略空气阻力和钉子直径，不计绳被钉子阻挡和绳断裂时的机械能损失。

（1）若碰后，B在竖直面内做圆周运动，且能经过圆周运动最高点，求B碰后瞬间速度的最小值；

（2）若改变A碰前瞬间的速度，碰后A运动到P点停止，B在竖直面圆周运动旋转2圈，经过M正下方时细绳子断开，B也来到P点，求B碰后瞬间的速度大小；

（3）若拉力达到12mg细绳会断，上下移动N的位置，保持N在M正上方，B碰后瞬间的速度与（2）间中的相同，使B旋转n圈。经过M正下的时细绳断开，求MN之间距离的范围，及在n的所有取值中，B落在地面时水平位移的最小值和最大值。

查看解析收藏纠错

+选题
29. 水平圆盘上紧贴边缘放置一密度均匀的小圆柱体，如图（a）所示，图（b）为俯视图，测得圆盘直径D = 42.02cm，圆柱体质量m = 30.0g，圆盘绕过盘心O₁的竖直轴匀速转动，转动时小圆柱体相对圆盘静止。
为了研究小圆柱体做匀速圆周运动时所需要的向心力情况，某同学设计了如下实验步骤：

（1）用秒表测圆盘转动10周所用的时间t = 62.8s，则圆盘转动的角速度ω = rad/s（π取3.14）

（2）用游标卡尺测量小圆柱体不同位置的直径，某次测量的示数如图（c）所示，该读数d = mm，多次测量后，得到平均值恰好与d相等。

（3）写出小圆柱体所需向心力表达式F = （用D、m、ω、d表示），其大小为N（保留2位有效数字）

查看解析收藏纠错

+选题
30. 如图所示空间原有大小为E、方向竖直向上的强电场，在此空间同一水平面的 M、N点固定两个等量异种点电荷，绝缘光滑圆环ABCD垂直MN放置，其圆心O在MN的中点，半径为R、AC 和BD分别为竖直和水平的直径。质量为 m、电荷量为+q的小球套在圆环上，从A 点沿圆环以初速度V₀做完整的圆周运动，则（）

A . 小球从A 到 C的过程中电势能减少 B . 小球不可能沿圆环做匀速圆周运动 C . 可求出小球运动到 B 点时的加速度 D . 小球在D 点受到圆环的作用力方向平行 MN

查看解析收藏纠错

+选题
31. 如图所示，光滑水平轨道AB与竖直面内的光滑半圆形轨道BC在B点平滑连接．一小物体将轻弹簧压缩至A点后由静止释放，物体脱离弹簧后进入半圆形轨道，恰好能够到达最高点C．下列说法正确的是（）

A . 物体在C点所受合力为零 B . 物体在C点的速度为零 C . 物体在C点的向心加速度等于重力加速度 D . 物体在A点时弹簧的弹性势能等于物体在C点的动能

查看解析收藏纠错

+选题
32. 如图，一光滑大圆环固定在竖直平面内，质量为m的小环套在大圆环上，小环从静止开始由大圆环顶端经Q点自由下滑至其底部，Q为竖直线与大圆环的切点。则小环下滑过程中对大圆环的作用力大小（　　）

A . 在Q点最大 B . 在Q点最小 C . 先减小后增大 D . 先增大后减小

查看解析收藏纠错

+选题
33. 2024年5月，嫦娥六号探测器发射成功，开启了人类首次从月球背面采样返回之旅。将采得的样品带回地球，飞行器需经过月面起飞、环月飞行、月地转移等过程。月球表面自由落体加速度约为地球表面自由落体加速度的 $\text{[math]}$ 。下列说法正确的是（　　）

A . 在环月飞行时，样品所受合力为零 B . 若将样品放置在月球正面，它对月球表面压力等于零 C . 样品在不同过程中受到的引力不同，所以质量也不同 D . 样品放置在月球背面时对月球的压力，比放置在地球表面时对地球的压力小

查看解析收藏纠错

+选题
34. 如图，半径为 R 的圆环水平放置并固定，圆环内有质量为 m_A和 m_B的小球 A 和 B（m_A>m_B）。初始时小球 A 以初速度 v₀沿圆环切线方向运动，与静止的小球 B 发生碰撞。不计小球与圆环之间的摩擦，两小球始终在圆环内运动。

（1）若小球 A 与 B 碰撞后结合在一起，求碰撞后小球组合体的速度大小及做圆周运动所需向心力的大小；

（2）若小球 A 与 B 之间为弹性碰撞，且所有的碰撞位置刚好位于等边三角形的三个顶点，求小球的质量比 $\text{[math]}$ 。

（3）若小球 A 与 B 之间为非弹性碰撞，每次碰撞后的相对速度大小为碰撞前的相对速度大小的 e 倍（0<e<1），求第 1 次碰撞到第 2n+1 次碰撞之间小球 B 通过的路程。

查看解析收藏纠错

+选题
35. 如图所示. 在细绳的拉动下，半径为 $\text{[math]}$ 的卷轴可绕其固定的中心点 $\text{[math]}$ 在水平面内转动. 卷轴上沿半径方向固定着长度为 $\text{[math]}$ 的细管，管底在 $\text{[math]}$ 点. 细管内有一根原长为 $\text{[math]}$ 、劲度系数为 $\text{[math]}$ 的轻质弹簧，弹簧底端固定在管底，顶端连接质量为 $\text{[math]}$ 、可视为质点的插销. 当以速度 $\text{[math]}$ 匀速拉动细绳时，插销做匀速圆周运动. 若 $\text{[math]}$ 过大，插销会卡进固定的端盖，使卷轴转动停止. 忽略摩擦力，弹簧在弹性限度内. 要使卷轴转动不停止， $\text{[math]}$ 的最大值为 $\text{[math]}$

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
36. 如图所示，细绳穿过竖直的管子拴住一个小球，让小球在A高度处的水平面内做匀速圆周运动，现用力将细绳缓慢下拉，使小球在B高度处的水平面内做匀速圆周运动，不计一切摩擦，则（　　）

A . 线速度v_A＞v_B B . 角速度ω_A＜ω_B C . 向心加速度a_A＜a_B D . 向心力F_A＞F_B

查看解析收藏纠错

+选题

小题精练 07 圆周运动问题-备考2025年高考物理题型突破讲练

一、圆周运动基本量

二、水平面的圆周运动

三、竖直面的圆周运动

四、破鼎提升

五、直击高考

相关试卷收起∨

小题精练 07 圆周运动问题-备考2025年高考物理题型突破讲练

一、圆周运动基本量

二、水平面的圆周运动

三、竖直面的圆周运动

四、破鼎提升

五、直击高考

相关试卷 收起∨

相关试卷收起∨