大题精练-02 力学三大观点的综合应用问题-备考2025年高考物理题型突破讲练

1. 如图所示，A、B两个物体相互接触，但并不黏合，放置在水平面上，水平面与物体间的摩擦力可忽略，两物体的质量 $\text{[math]}$ 为4kg， $\text{[math]}$ 为6kg。从 $\text{[math]}$ 开始，推力 $\text{[math]}$ 和拉力 $\text{[math]}$ 分别作用于A、B上， $\text{[math]}$ 、 $\text{[math]}$ 随时间的变化规律为 $\text{[math]}$ ， $\text{[math]}$ ，下列说法正确的是（　　）

A . A、B始终做匀变速直线运动 B . A对B的作用力大于B对A的作用力 C . t =1.5s时A的速度小于1.5m/s D . t =2s时A、B开始分离

查看解析收藏纠错

+选题
2. 在水平冰面上，狗拉着雪橇做匀速圆周运动，O点为圆心。能正确地表示雪橇受到的牵引力F及摩擦力f的选项是（　　）

A . B . C . D .

查看解析收藏纠错

+选题
3. 如图所示，质量为2kg的物体A静止在劲度系数为 $\text{[math]}$ 的竖直轻弹簧上方，质量为3kg的物体B用细线悬挂起来，物体A、B紧挨在一起但A、B之间无压力。某时刻将细线剪断，则在细线被剪断的瞬间，下列说法正确的是（　　）（当地重力加速度 $\text{[math]}$ ）

A . 轻弹簧的压缩量为0.5m B . 物体A、B的瞬时加速度大小为 $\text{[math]}$ C . 物体B的瞬时加速度大小为 $\text{[math]}$ D . 物体B对物体A的压力大小为30N

查看解析收藏纠错

+选题
4. 如图所示，质量为 $\text{[math]}$ 的斜面体 $\text{[math]}$ 放在水平面上，质量为 $\text{[math]}$ 的重物 $\text{[math]}$ 放在斜面体 $\text{[math]}$ 上，质量为 $\text{[math]}$ 的重物 $\text{[math]}$ 通过水平细绳与重物 $\text{[math]}$ 相连于 $\text{[math]}$ 点， $\text{[math]}$ 点通过另一根细绳悬挂于天花板上，细绳与竖直方向夹角以及斜面体倾角均为 $\text{[math]}$ ， $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 都处于静止状态。 $\text{[math]}$ 取 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 求：

（1）水平细绳 $\text{[math]}$ 的拉力大小；

（2）重物 $\text{[math]}$ 对斜面体 $\text{[math]}$ 的压力及摩擦力大小；

（3）地面对斜面体 $\text{[math]}$ 的支持力及摩擦力大小。

查看解析收藏纠错

+选题

5. 如图所示，一个质量为m的物体（可视为质点）以某一速度从A点冲上倾角为 $\text{[math]}$ 的固定斜面，其运动的加速度为 $\text{[math]}$ ，物体在斜面上上升的最大高度为h，则在这个过程中物体（　　）

A . 重力势能增加了 $\text{[math]}$ B . 重力势能减少了 $\text{[math]}$ C . 动能损失了 $\text{[math]}$ D . 机械能损失了 $\text{[math]}$

查看解析收藏纠错

+选题
6. 如图，轻质定滑轮固定在天花板上，物体 $\text{[math]}$ 和 $\text{[math]}$ 用不可伸长的轻绳相连，悬挂在定滑轮上，质量 $\text{[math]}$ ， $\text{[math]}$ 时刻将两物体由静止释放，物体 $\text{[math]}$ 的加速度大小为 $\text{[math]}$ 。 $\text{[math]}$ 时刻轻绳突然断开，物体 $\text{[math]}$ 能够达到的最高点恰与物体 $\text{[math]}$ 释放位置处于同一高度，取 $\text{[math]}$ 时刻物体 $\text{[math]}$ 所在水平面为零势能面，此时物体 $\text{[math]}$ 的机械能为 $\text{[math]}$ 。重力加速度大小为 $\text{[math]}$ ，不计摩擦和空气阻力，两物体均可视为质点。下列说法正确的是（　　）

A . 物体 $\text{[math]}$ 和 $\text{[math]}$ 的质量之比为 $\text{[math]}$ B . $\text{[math]}$ 时刻物体 $\text{[math]}$ 的机械能为 $\text{[math]}$ C . $\text{[math]}$ 时刻物体 $\text{[math]}$ 重力的功率为 $\text{[math]}$ D . $\text{[math]}$ 时刻物体 $\text{[math]}$ 的速度大小 $\text{[math]}$

查看解析收藏纠错

+选题
7. 如图所示，倾角 $\text{[math]}$ 为 $\text{[math]}$ 的斜劈静止在水平面上，从与斜劈顶点 $\text{[math]}$ 等高的 $\text{[math]}$ 点抛出一小球，其初速度 $\text{[math]}$ 大小为 $\text{[math]}$ ，方向与水平方向夹角 $\text{[math]}$ 为 $\text{[math]}$ ，小球刚好从 $\text{[math]}$ 点沿斜劈向下运动。忽略一切摩擦和空气阻力，重力加速度 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 。下列说法正确的是（）

A . 小球从抛出到落在斜劈上的时间为 $\text{[math]}$ B . $\text{[math]}$ 、 $\text{[math]}$ 两点间的距离为 $\text{[math]}$ C . 小球在斜劈上运动过程中，小球机械能守恒 D . 小球在斜劈上运动过程中，斜劈对小球做负功

查看解析收藏纠错

+选题
8. 质量为2kg的物块静止于水平面上， $\text{[math]}$ 时刻施加一水平拉力，拉力随时间变化的关系如图所示。已知物块与水平面之间的动摩擦因数为0.4，最大静摩擦力等于滑动摩擦力，g取 $\text{[math]}$ 。下列选项正确的是（　　）

A . 0~2s内重力的冲量为零 B . 0~1s内摩擦力冲量的大小为 $\text{[math]}$ C . $\text{[math]}$ 时物块的动量为零 D . $\text{[math]}$ 时物块动量的大小为 $\text{[math]}$

查看解析收藏纠错

+选题
9. 清洗汽车的高压水枪如图所示。水枪喷出的水柱截面是直径为D的圆形，水流速度为v，水柱垂直射向汽车表面，冲击汽车后速度减为零。已知水的密度为ρ。则（）

A . 高压水枪单位时间喷出的水的质量为 $\text{[math]}$ B . 高压水枪单位时间内对汽车的作用力为 $\text{[math]}$ C . 水柱对汽车的压强为ρv³ D . 高压水枪单位时间内喷出水的动能为 $\text{[math]}$

查看解析收藏纠错

+选题
10. 如图所示，光滑水平面上质量为2M的物体A以速度v向右匀速滑动，质量为M的B物体左端与轻质弹簧连接并静止在光滑水平面上，在物体A与弹簧接触后，以下判断正确的是（　　）

A . 在物体A与弹簧接触过程中，弹簧对A的弹力冲量大小为 $\text{[math]}$ B . 在物体A与弹簧接触过程中，弹簧对B的弹力做功的功率一直增大 C . 从A与弹簧接触到A、B相距最近的过程中，弹簧对A、B做功的代数和为0 D . 从A与弹簧接触到A、B相距最近的过程中，最大弹性势能为 $\text{[math]}$

查看解析收藏纠错

+选题
11. 如图所示，光滑的水平面上，子弹以速度 $\text{[math]}$ 射入木块，最后留在木块中随木块一起匀速运动，子弹所受阻力恒定不变，下列说法正确的是（）

A . 子弹和木块系统动量守恒 B . 子弹和木块系统机械能守恒 C . 子弹对木块做的功大于木块对子弹做的功 D . 子弹对木块做的功等于木块对子弹做的功

查看解析收藏纠错

+选题
12. 如图所示，光滑水平面上有外形相同的A、B两个物体均向左运动，物体A的动量p₁=5kg·m/s，物体B的动量p₂=7kg·m/s，在物体A与物体B发生对心碰撞后物体B的动量变为10kg·m/s，则A、B两个物体的质量m₁与m₂间的关系可能是（　　）

A . m₁=m₂ B . m₁= $\text{[math]}$ m₂ C . m₁= $\text{[math]}$ m₂ D . m₁= $\text{[math]}$ m₂

查看解析收藏纠错

+选题
13. 如图所示，将带负电荷，电荷量 $\text{[math]}$ 、质量 $\text{[math]}$ 的滑块放在小车的水平绝缘板的左端，小车的质量 $\text{[math]}$ ，滑块与绝缘板间的动摩擦因数 $\text{[math]}$ ，小车的绝缘板足够长，它们所在的空间存在磁感应强度 $\text{[math]}$ 的水平方向的匀强磁场（垂直于纸面向里）。开始时小车静止在光滑水平面上，一轻质细绳长 $\text{[math]}$ ，一端固定在O点，另一端与质量 $\text{[math]}$ 的小球相连，把小球从水平位置由静止释放，当小球运动到最低点时与小车相撞（碰撞时间很短），碰撞后小球恰好静止，g取 $\text{[math]}$ 。求：

（1）与小车碰撞前小球到达最低点时细线对小球的拉力大小：

（2）小球与小车的碰撞过程中系统损失的机械能 $\text{[math]}$ ；

（3）碰撞后小车的最终速度。

查看解析收藏纠错

+选题
14. 如图所示，质量均为 $\text{[math]}$ 的木块 $\text{[math]}$ 和 $\text{[math]}$ ，并排放在光滑水平桌面上， $\text{[math]}$ 上固定一竖直轻杆，轻杆上端的 $\text{[math]}$ 点系一长度为 $\text{[math]}$ 的细线，细线另一端系一质量为 $\text{[math]}$ 的球 $\text{[math]}$ 。现将 $\text{[math]}$ 球拉起使细线水平伸直，并由静止释放 $\text{[math]}$ 球（ $\text{[math]}$ 球不与直杆相碰），重力加速度 $\text{[math]}$ 。求：

（1） $\text{[math]}$ 球第一次运动到最低点时的速度大小；

（2）当 $\text{[math]}$ 球第一次运动到最低点，木块 $\text{[math]}$ 向右移动的距离；

（3） $\text{[math]}$ 两木块分离后， $\text{[math]}$ 球偏离竖直方向的最大偏角 $\text{[math]}$ 的余弦值 $\text{[math]}$ 。

查看解析收藏纠错

+选题
15. 如图所示，两个质量分别为 $\text{[math]}$ 、 $\text{[math]}$ 的小物块A、B（均可视为质点）静置于水平地面上，中间用细线相连，且中间夹着一个劲度系数很大的压缩轻弹簧（长度忽略不计），弹簧左端与A相连，弹簧右端与B接触但不相连，此时弹簧的弹性势能为48J。紧邻A、B两侧各有长 $\text{[math]}$ 的光滑水平地面，以F点和C点为分界点，F点左侧地面和两物块间的动摩擦因数均为 $\text{[math]}$ ， C点右侧固定有一半径为R的光滑半圆轨道，该轨道在C点刚好和水平地面相切。突然剪断A、B间的细线，B能够经过半圆轨道顶端D点，且B落地后不反弹，重力加速度g取 $\text{[math]}$ ，不计空气阻力，求：

（1） A停止运动时到F点的距离；

（2）只改变R的大小，使B从D点脱离后落地时距离C点最远，求此时R的大小。

查看解析收藏纠错

+选题

16. 一端连接轻质弹簧的物体B静止在光滑水平面上（如图甲所示）。物体A以速度v向右运动压缩弹簧，弹簧的最大压缩量为x，现让该弹簧一端连接另一物体C（如图乙所示），物体A以2v的速度向右压缩弹簧，弹簧的最大压缩量仍为x，知A、B的质量均为m，则（）

A . 物体C的质量为 $\text{[math]}$ m B . 物体C的质量为 $\text{[math]}$ m C . 物体C的最终速度为 $\text{[math]}$ v D . 物体C的最终速度为 $\text{[math]}$ v

查看解析收藏纠错

+选题
17. 如图所示，质量 $\text{[math]}$ 、上表面粗糙的长木板静止在光滑的水平面上， $\text{[math]}$ 时，质量 $\text{[math]}$ 表面粗糙的物块（可视为质点）以初速度 $\text{[math]}$ 滑上长木板，经过时间 $\text{[math]}$ 物块和长木板达到共同速度，此后以共同速度匀速运动，重力加速度大小为 $\text{[math]}$ ，则（）

A . 长木板做匀加速运动的加速度大小为 $\text{[math]}$ B . 物块与长木板之间动摩擦因数为0.1 C . 长木板长度至少为 $\text{[math]}$ D . 物块与长木板组成的系统损失机械能为 $\text{[math]}$

查看解析收藏纠错

+选题
18. 如图所示，光滑水平面上有一个质量为 $\text{[math]}$ 的长方形薄木板，一个可视为质点的质量为 $\text{[math]}$ 的物块从木板左边以速度 $\text{[math]}$ 滑上木板。设物块与木板之间的动摩擦因数为 $\text{[math]}$ ，木板长度为 $\text{[math]}$ ，则下列说法正确的是（　　）

A . 当 $\text{[math]}$ 时，物块一定不会从木板上滑落 B . 当 $\text{[math]}$ 时，物块一定不会从木板上滑落 C . 当 $\text{[math]}$ 时，物块一定会从木板上滑落 D . 当 $\text{[math]}$ 时，物块一定会从木板上滑落

查看解析收藏纠错

+选题
19. 如图，质量为M的小车静止在光滑水平面上，小车AB段是半径为R的四分之一光滑圆弧轨道，BC段是长为L的粗糙水平轨道，两段轨道相切于B点。一质量为m的可视为质点的滑块，从小车上的A点由静止开始沿轨道下滑，然后滑入BC轨道，最后恰好停在C点。已知小车质量M=5m，滑块与轨道BC间的动摩擦因数为 $\text{[math]}$ ，重力加速度为g，则（　　）

A . 全过程滑块在水平方向上相对地面的位移的大小为R+L B . 全过程小车相对地面的位移大小为 $\text{[math]}$ C . 小车在运动过程中速度的最大值为 $\text{[math]}$ D . $\text{[math]}$ 、L、R三者之间的关系为 $\text{[math]}$

查看解析收藏纠错

+选题
20. 如图所示，曲面为四分之一圆弧、质量为2m光滑滑块静止在水平地面上，一质量为m的小球以水平初速度 $\text{[math]}$ 冲上滑块。重力加速度为g，求：

（1）小球上升的最大高度h；

（2）小球与滑块水平方向的速度分别为 $\text{[math]}$ 、 $\text{[math]}$ ，通过计算作出小球在滑块上运动过程中滑块 $\text{[math]}$ 随小球 $\text{[math]}$ 的变化图像，标明图线特殊位置的坐标值。

查看解析收藏纠错

+选题
21. 如图所示，在光滑水平地面上放置着一半径为R的 $\text{[math]}$ 圆弧形滑块B，其弧面光滑，在滑块B的右侧放置一连接有轻质弹簧的小球C。现让小球A从滑块B的正上方距地面高h=2R处由静止释放，小球沿滑块B的切线进入圆弧面，然后从滑块B的末端水平滑出，之后小球A挤压弹簧但与弹簧未粘连。已知小球A的质量为m ，小球C的质量为4m ，滑块B的质量为km（k>1），重力加速度为g。

（1）小球A从滑块B末端滑出时，求小球A和滑块B的速度分别为多少？

（2）小球A挤压弹簧过程中，求弹簧最大的弹性势能；

（3）要使小球A弹回后能追上滑块B，则k的取值范围。

查看解析收藏纠错

+选题

22. 如图所示，质量为2m的木板C静止在光滑水平面上。现将速度分别为v₀、2v₀的木块A、B同时放上木板，运动方向如图，木块的质量均为m，A、B间的距离为d，木块与木板之间的动摩擦因数均为μ，木板足够长，重力加速度取g，求：

（1）木块A在木板C上的滑行时间t；

（2）木块A、B运动过程中因摩擦产生的总热量Q；

（3）运动过程中木块A和木块B间的最大距离L。

查看解析收藏纠错

+选题
23. 如图所示，用不可伸长的、长度为 $\text{[math]}$ 的轻绳将小球 $\text{[math]}$ 悬挂于 $\text{[math]}$ 点，用不可伸长的、长度为 $\text{[math]}$ （未知）的轻绳将小球 $\text{[math]}$ 悬于 $\text{[math]}$ 点，静止时小球 $\text{[math]}$ 刚好与光滑水平面接触，现将轻绳拉至水平并刚好
伸直，将小球 $\text{[math]}$ 由静止释放，当小球 $\text{[math]}$ 运动至最低点时，与静止在光滑水平面上的物块 $\text{[math]}$ 发生弹性正碰，碰撞后物块 $\text{[math]}$ 向右滑动并与小球 $\text{[math]}$ 发生弹性碰撞．已知小球 $\text{[math]}$ 、 $\text{[math]}$ 的质量均为 $\text{[math]}$ ，物块 $\text{[math]}$ 的质量为 $\text{[math]}$ ， $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 均可视为质点，重力加速度大小为 $\text{[math]}$ ，不计空气阻力．求：

（1） $\text{[math]}$ 与 $\text{[math]}$ 碰撞前瞬间，小球 $\text{[math]}$ 的速度大小；

（2） $\text{[math]}$ 与 $\text{[math]}$ 碰撞后一瞬间，物块 $\text{[math]}$ 的速度大小；

（3） $\text{[math]}$ 与 $\text{[math]}$ 碰撞后， $\text{[math]}$ 运动过程中绳子始终不松弛时 $\text{[math]}$ 的取值范围．

查看解析收藏纠错

+选题
24. 如图所示，光滑水平平台AB右端与顺时针转动的水平传送带BC平滑无缝连接，BC长度L=2m。在平台AB上静止着a、b、c三个小滑块，a、b滑块间有一被压缩的轻弹簧（滑块与轻弹簧不拴接）。释放弹簧，弹簧与滑块a、b分离后a的速度v₀=4m/s（此时a未滑上传送带，b未与c碰撞），a从传送带右端离开后，落在水平地面上的D点，b与c碰撞后结合在一起。已知a、b ， c的质量分别为m_a=0.5kg、m_b=0.2kg、m_c=0.2kg，a与传送带间的动摩擦因数μ=0.5，C点距地面高h=0.8m，滑块均可视为质点，g取10m/s²。

（1）求轻弹簧的最大弹性势能E_p；

（2）求b、c碰撞过程中损失的机械能；

（3）若传送带的速度可在2m/s<v<8m/s间调节；求a落点D与C点间水平距离x的大小（结果可以含有v）；

（4）若a脱离弹簧后，将弹簧撤去，并立即在a的左侧固定一竖直挡板，同时传送带调整为以4m/s的速度逆时针方向转动（此时a还没有滑上传送带），后续a每次与挡板相碰，均以碰前速度的一半反弹，求a在传动带上相对传送带运动的总路程s。

查看解析收藏纠错

+选题
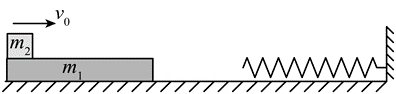
25. 如图甲所示，在光滑水平面上放有一左端固定在墙壁上的轻质弹簧，弹簧处于原长时右端恰好位于A点，弹簧所在的光滑水平面与水平传送带在A点平滑连接。传送带长 $\text{[math]}$ ，且以 $\text{[math]}$ 的速率沿顺时针方向匀速转动，传送带右下方有一固定在光滑地面上半径为 $\text{[math]}$ 、圆心角 $\text{[math]}$ 的圆弧轨道，圆弧轨道右侧紧挨着一个与轨道等高，质量 $\text{[math]}$ 的长木板（木板厚度不计）。现将一质量 $\text{[math]}$ 的滑块Q（Q视为质点且与弹簧未拴接）向左压缩弹簧至图中 $\text{[math]}$ 点后由静止释放，滑块Q从A点滑上传送带，并从传送带右端 $\text{[math]}$ 点离开，恰好沿 $\text{[math]}$ 点的切线方向进入与传送带在同一竖直面的圆弧轨道CD，然后无动能损失滑上长木板。已知弹簧弹力与滑块Q在GA段的位移关系如图乙所示，滑块Q与传送带、长木板间的动摩擦因数均为 $\text{[math]}$ ，重力加速度大小 $\text{[math]}$ 。

（1）求滑块Q刚滑上传送带时的速度大小 $\text{[math]}$ ；

（2）若滑块Q运动至圆弧轨道最低点 $\text{[math]}$ 时，轨道对其的支持力为 $\text{[math]}$ ，且滑块恰好未滑离长木板，求长木板的长度 $\text{[math]}$ ；

（3）若去掉圆弧轨道和长木板，滑块Q从传送带上滑落地面并与地面发生碰撞，每次碰撞前后水平方向速度大小不变，且每次反弹的高度是上一次的三分之二，不计空气阻力。求滑块Q与地面发生 $\text{[math]}$ 次碰撞后前 $\text{[math]}$ 次损失的机械能 $\text{[math]}$ 与 $\text{[math]}$ 的函数关系式。

查看解析收藏纠错

+选题

26. 如图所示，质量为m的小球A用一不可伸长的轻绳悬挂在O点，在O点正下方的光滑桌面上有一个与A完全相同的静止小球B，B距O点的距离等于绳长L。现将A拉至某一高度，由静止释放，A以速度v在水平方向和B发生正碰并粘在一起。重力加速度为g。求：

（1） A释放时距桌面的高度H；

（2）碰撞前瞬间绳子的拉力大小F；

（3）碰撞过程中系统损失的机械能 $\text{[math]}$ 。

查看解析收藏纠错

+选题
27. 如图所示，有一固定的光滑 $\text{[math]}$ 圆弧轨道，半径 $\text{[math]}$ ，一质量为 $\text{[math]}$ 的小滑块B从轨道顶端滑下，在其冲上长木板C左端时，给木板一个与小滑块相同的初速度，已知 $\text{[math]}$ ， B、C间动摩擦因数 $\text{[math]}$ ， C与地面间的动摩擦因数 $\text{[math]}$ ， C右端有一个挡板，C长为 $\text{[math]}$ 。

求：

（1） $\text{[math]}$ 滑到 $\text{[math]}$ 的底端时对 $\text{[math]}$ 的压力是多大？

（2）若 $\text{[math]}$ 末与 $\text{[math]}$ 右端挡板碰撞，当 $\text{[math]}$ 与地面保持相对静止时， $\text{[math]}$ 间因摩擦产生的热量是多少？

（3）在 $\text{[math]}$ 时，B与C右端挡板发生碰撞，且碰后粘在一起，求 $\text{[math]}$ 从滑上 $\text{[math]}$ 到最终停止所用的时间。

查看解析收藏纠错

+选题
28. 如图，质量m₁=1kg 的木板静止在光滑水平地面上，右侧的竖直墙面固定一劲度系数k=20N/m 的轻弹簧，弹簧处于自然状态。质量m₂=4kg 的小物块以水平向右的速度 $\text{[math]}$ 滑上木板左端，两者共速时木板恰好与弹簧接触。木板足够长，物块与木板间的动摩擦因数μ=0.1，最大静摩擦力等于滑动摩擦力。弹簧始终处在弹性限度内，弹簧的弹性势能 Ep与形变量x 的关系为 $\text{[math]}$ 。取重力加速度g=10m/s² ，结果可用根式表示。

（1）求木板刚接触弹簧时速度v，的大小及木板运动前右端距弹簧左端的距离x₁。

（2）求木板与弹簧接触以后，物块与木板之间即将相对滑动时弹簧的压缩量x₂及此时木板速度v₂的大小。

（3）已知木板向右运动的速度从v₂减小到0所用时间为t₀。求木板从速度为v₂ 时到之后与物块加速度首次相同时的过程中，系统因摩擦转化的内能△U（用t表示）。

查看解析收藏纠错

+选题
29. 如图，一竖直固定的长直圆管内有一质量为M的静止薄圆盘，圆盘与管的上端口距离为l，圆管长度为20l。一质量为 $\text{[math]}$ 的小球从管的上端口由静止下落，并撞在圆盘中心，圆盘向下滑动，所受滑动摩擦力与其所受重力大小相等。小球在管内运动时与管壁不接触，圆盘始终水平，小球与圆盘发生的碰撞均为弹性碰撞且碰撞时间极短。不计空气阻力，重力加速度大小为g。求：

（1）第一次碰撞后瞬间小球和圆盘的速度大小；

（2）在第一次碰撞到第二次碰撞之间，小球与圆盘间的最远距离；

（3）圆盘在管内运动过程中，小球与圆盘碰撞的次数。

查看解析收藏纠错

+选题
30. 如图，L形滑板A静置在粗糙水平面上，滑板右端固定一劲度系数为 $\text{[math]}$ 的轻质弹簧，弹簧左端与一小物块B相连，弹簧处于原长状态。一小物块C以初速度 $\text{[math]}$ 从滑板最左端滑入，滑行 $\text{[math]}$ 后与B发生完全非弹性碰撞（碰撞时间极短），然后一起向右运动；一段时间后，滑板A也开始运动．已知A、B、C的质量均为 $\text{[math]}$ ，滑板与小物块、滑板与地面之间的动摩擦因数均为 $\text{[math]}$ ，重力加速度大小为 $\text{[math]}$ ；最大静摩擦力近似等于滑动摩擦力，弹簧始终处于弹性限度内。求：

（1） C在碰撞前瞬间的速度大小；

（2） C与B碰撞过程中损失的机械能；

（3）从C与B相碰后到A开始运动的过程中，C和B克服摩擦力所做的功。

查看解析收藏纠错

+选题

大题精练-02 力学三大观点的综合应用问题-备考2025年高考物理题型突破讲练

一、动力学专项

二、冲量与动量、功和能

三、几种“类碰撞”问题

四、破鼎提升

五、直击高考

相关试卷收起∨

大题精练-02 力学三大观点的综合应用问题-备考2025年高考物理题型突破讲练

一、动力学专项

二、冲量与动量、功和能

三、几种“类碰撞”问题

四、破鼎提升

五、直击高考

相关试卷 收起∨

相关试卷收起∨