内蒙古呼伦贝尔市海拉尔区2021年中考数学模拟试卷

修改时间：2024-07-13 浏览次数：220 类型：中考模拟编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、单选题

1. 2的倒数是（）

A . 2 B . ﹣2 C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
2. 下列运算正确的是（）

A . 5m+2m=7m² B . ﹣2m²•m³=2m⁵ C . （﹣a²b）³=﹣a⁶b³ D . （b+2a）（2a﹣b）=b²﹣4a²

查看解析收藏纠错

+选题
3. H7N9病毒直径为30纳米，已知1纳米＝0.000 000 001米．用科学记数法表示这个病毒直径的大小，正确的是（）

A . $\text{[math]}$ 米 B . $\text{[math]}$ 米 C . $\text{[math]}$ 米 D . $\text{[math]}$ 米

查看解析收藏纠错

+选题
4. 如果一组数据为 $\text{[math]}$ ，0，1，0，0，那么下列说法错误的是（）

A . 这组数据的方差是0 B . 这组数据的众数是0 C . 这组数据的中位数是0 D . 这组数据的平均数是0

查看解析收藏纠错

+选题
5. 如图，已知直线 $\text{[math]}$ ，一块含30°角的直角三角板如图所示放置， $\text{[math]}$ ，则 $\text{[math]}$ 等于（）

A . 25° B . 35° C . 40° D . 45°

查看解析收藏纠错

+选题
6. 如图在平面直角坐标系中，点A、B、C的坐标分别为（﹣1，3）、（﹣4，1）、（﹣2，1），将△ABC沿一确定方向平移得到△A₁B₁C₁ ，点B的对应点B₁的坐标是（1，2），则点C对应的点C₁的坐标是（）

A . C₁（2，2） B . C₁（2，1） C . C₁（2，3） D . C₁（3，2）

查看解析收藏纠错

+选题
7. 若关于 $\text{[math]}$ 的不等式组 $\text{[math]}$ 的解集是 $\text{[math]}$ ，则 $\text{[math]}$ 的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
8. 一个物体的三视图如图所示，根据图中的数据，可求这个物体的侧面积为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
9. 如图，已知⊙O的半径是2，点A，B，C在⊙O上，若四边形OABC为菱形，则图中阴影部分面积为（）

A . $\text{[math]}$ π﹣2 $\text{[math]}$ B . $\text{[math]}$ π﹣ $\text{[math]}$ C . $\text{[math]}$ π﹣2 $\text{[math]}$ D . $\text{[math]}$ π﹣ $\text{[math]}$

查看解析收藏纠错

+选题
10. 如图，平行于 $\text{[math]}$ 轴的直线分别交 $\text{[math]}$ 与 $\text{[math]}$ 的图像于点 $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 是 $\text{[math]}$ 轴上的点，则 $\text{[math]}$ 的面积为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
11. 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 于点D.点 $\text{[math]}$ 从点A出发，沿 $\text{[math]}$ 的路径运动，运动到点C停止，过点 $\text{[math]}$ 作 $\text{[math]}$ 于点E，作 $\text{[math]}$ 于点F.设点P运动的路程为x，四边形 $\text{[math]}$ 的面积为y，则能反映y与x之间函数关系的图象是（）

A . B . C . D .

查看解析收藏纠错

+选题
12. 在平面直角坐标系中，长为2的线段 $\text{[math]}$ （点D在点C右侧）在x轴上移动 $\text{[math]}$ ， $\text{[math]}$ ，连接 $\text{[math]}$ 、 $\text{[math]}$ ，则 $\text{[math]}$ 的最小值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题

二、填空题

13. 在函数 $\text{[math]}$ 中，自变量x的取值范围是。

查看解析收藏纠错

+选题
14. 分解因式：x²（x﹣3）﹣x+3＝.

查看解析收藏纠错

+选题
15. 若 $\text{[math]}$ ，则 $\text{[math]}$ 的值为．

查看解析收藏纠错

+选题
16. 某工厂新引进一批电子产品，甲工人比乙工人每小时多搬运30件电子产品，已知甲工人搬运300件电子产品所用的时间与乙工人搬运200件电子产品所用的时间相同 $\text{[math]}$ 若设乙工人每小时搬运 $\text{[math]}$ 件电子产品，可列方程为．

查看解析收藏纠错

+选题
17. 如图，正方形ABCD的边长为6，点O是对角线AC、BD的交点.点E在CD上，且DE=2CE，连接BE.过点C作CF⊥BE，垂足是F，连接OF，则OF的长为.

查看解析收藏纠错

+选题

三、解答题

18. 计算： $\text{[math]}$

查看解析收藏纠错

+选题
19. 先化简： $\text{[math]}$ ，再从－1，1，2中选择一个适当的数作为x的值代入求值.

查看解析收藏纠错

+选题
20. 如图， $\text{[math]}$ 在平面内绕点B逆时针旋转 $\text{[math]}$ 得到 $\text{[math]}$ ．已知 $\text{[math]}$ ，连接DE

（1）求证： $\text{[math]}$

（2）试判断四边形ABED的形状，并说明理由．

查看解析收藏纠错

+选题
21. 如图所示，在某海域，一艘指挥船在C处收到渔船在B处发出的求救信号，经确定，遇险抛锚的渔船所在的B处位于C处的南偏西45°方向上，且BC＝60海里；指挥船搜索发现，在C处的南偏西60°方向上有一艘海监船A，恰好位于B处的正西方向．于是命令海监船A前往搜救，已知海监船A的航行速度为30海里/小时，问渔船在B处需要等待多长时间才能得到海监船A的救援？（结果保留根号）

查看解析收藏纠错

+选题
22. 为庆祝中国共产党建党100周年，讴歌中华民族实现伟大复兴的奋斗历程，继承革命先烈的优良传统．某中学开展了建党100周年知识测试．随机抽取了40名学生的测试成绩，并对成绩（等级制）进行整理、描述和分析．（说明：测试成绩均取整数，A级：10分，B级：9分，C级：8分，D级：7分及以下）
整理、描述样本数据，绘制统计表如下：

建党100周年知识测试成绩频数统计表

成绩等级

A

B

C

D

人数（名）

12

6

4

建党100周年知识测试扇形统计图

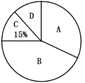
根据统计表、统计图中的信息，解答下列问题：

（1）补全统计表，并求出成绩为B级同学所占圆心角的度数；

（2）若该校共有520名学生参加建党100周年知识测试，成绩不低于9分为“优秀”，请估计该校参加建党100周年知识测试成绩达到优秀的学生有多少名？

（3）甲、乙、丙、丁是建党100周年知识测试成绩为10分的四名学生，学校计划从这四名学生中随机选出两名学生代表学校去参加全市中学生“建党100周年知识测试”竞赛，用列表法或画树状图法，求甲、乙两名学生中至少有一名被选中的概率．

查看解析收藏纠错

+选题
23. 如图，一次函数y＝k₁x+b与反比例函数y＝ $\text{[math]}$ 的图象交于A（2，m），B（n，﹣2）两点．过点B作BC⊥x轴，垂足为C，且S_△_ABC＝5．

（1）求一次函数与反比例函数的解析式；

（2）根据所给条件，请直接写出不等式k₁x+b＞ $\text{[math]}$ 的解集；

（3）若P（p，y₁），Q（﹣2，y₂）是函数y＝ $\text{[math]}$ 图象上的两点，且y₁≥y₂ ，求实数p的取值范围．

查看解析收藏纠错

+选题
24. 如图，M，N是以AB为直径的⊙O上的点，且 $\text{[math]}$ ＝ $\text{[math]}$ ，弦MN交AB于点C，BM平分∠ABD，MF⊥BD于点F.

（1）求证：MF是⊙O的切线；

（2）若CN＝3，BN＝4，求CM的长.

查看解析收藏纠错

+选题
25. 空气净化器越来越被人们认可，某商场购进A、B两种型号的空气净化器，如果销售5台A型和10台B型空气净化器的销售总价为20000元，销售10台A型和5台B型空气净化器的销售总价为17500元．

（1）求每台A型空气净化器和B型空气净化器的销售单价；

（2）该商场计划一次购进两种型号的空气净化器共100台，其中B型空气净化器的进货量不超过A型空气净化器的2倍，设购进A型空气净化器m台，这100台空气净化器的销售总价为y元．
①求y关于m的函数关系式；

②当销售总价最大时，该公司购进A型、B型空气净化器各多少台？

（3）在（2）的条件下，若A型空气净化器每台的进价为800元，B型空气净化器每台的进价z（元）满足z=-10m+700的关系式，则销售完这批空气净化器能获取的最大利润是多少元？

查看解析收藏纠错

+选题
26. 如图，抛物线 $\text{[math]}$ 与x轴交于点 $\text{[math]}$ ，点 $\text{[math]}$ ，与y轴交于点C，且过点 $\text{[math]}$ ．点P、Q是抛物线 $\text{[math]}$ 上的动点．

（1）求抛物线的解析式；

（2）当点P在直线OD下方时，求 $\text{[math]}$ 面积的最大值．

（3）直线OQ与线段BC相交于点E，当 $\text{[math]}$ 与 $\text{[math]}$ 相似时，求点Q的坐标．

查看解析收藏纠错

+选题

建党100周年知识测试成绩频数统计表
成绩等级	A	B	C	D
人数（名）	12		6	4

内蒙古呼伦贝尔市海拉尔区2021年中考数学模拟试卷

一、单选题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨