贵州省贵阳市花溪区2021年数学中考模拟试卷

修改时间：2024-07-13 浏览次数：260 类型：中考模拟编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、单选题

1. 四个实数0， $\text{[math]}$ 中，最小的数是（）

A . 0 B . $\text{[math]}$ C . $\text{[math]}$ D . -3.14

查看解析收藏纠错

+选题
2. 一副三角板如图摆放（直角顶点 $\text{[math]}$ 重合），边 $\text{[math]}$ 与 $\text{[math]}$ 交于点 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 等于（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
3. 如图的电路图上有4个开关 $\text{[math]}$ 和1个小灯泡下列操作中，“小灯泡发光”这个事件是随机事件的是（）

A . 只闭合1个开关 B . 只闭合2个开关 C . 只闭合3个开关 D . 闭合4个开关

查看解析收藏纠错

+选题
4. 在数轴上，点A，B在原点O的两侧，分别表示数a ， 2，将点A向右平移1个单位长度，得到点C．若CO=BO，则a的值为（）

A . -3 B . -2 C . -1 D . 1

查看解析收藏纠错

+选题
5. 如图，△ABC与△DEF位似，点O为位似中心.已知OA∶OD=1∶2，则△ABC与△DEF的面积比为（）

A . 1∶2 B . 1∶3 C . 1∶4 D . 1∶5

查看解析收藏纠错

+选题
6. 在同一平面直角坐标系中，两个一次函数 $\text{[math]}$ 与 $\text{[math]}$ 的图象相交，则其交点一定在（）

A . 第一象限 B . 第二象限 C . 第三象限 D . 第四象限

查看解析收藏纠错

+选题

7. 小强每天坚持引体向上锻炼，他记录了某一周每天做引体向上的个数，如下表：

星期	日	一	二	三	四	五	六
个数	11	12				13	12

其中有三天的个数墨汁覆盖了，但小强已经计算出这组数据唯一众数是13，平均数是12，那么这组数据的方差是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 1 D . $\text{[math]}$

查看解析收藏纠错

+选题

8. 如图，4张如图1的长为a，宽为b（a＞b）长方形纸片，按图2的方式放置，阴影部分的面积为S₁ ，空白部分的面积为S₂ ，若S₂＝2S₁ ，则a，b满足（）

A . a＝ $\text{[math]}$ B . a＝2b C . a＝ $\text{[math]}$ b D . a＝3b

查看解析收藏纠错

+选题
9. 小明有一个俯视图为等腰三角形的积木盒，现在积木盒中只剩下如图的9个空格，下面有四种积木的搭配，其中能恰好放入积木盒中空格的搭配有（）

A . 1种 B . 2种 C . 3种 D . 4种

查看解析收藏纠错

+选题
10. 某工厂生产的某种产品按质量分为10个档次，第1档次（最低档次）的产品一天能生产95件，每件利润6元，每提高一个档次，每件利润增加2元，但一天产量减少5件.若生产的产品一天的总利润为1120元，且同一天所生产的产品为同一档次，则该产品的质量档次是（）

A . 6 B . 8 C . 10 D . 12

查看解析收藏纠错

+选题
11. 尺规作图是初中数学学习中一个非常重要的内容.小明按以下步骤进行尺规作图：①将半径为 $\text{[math]}$ 的 $\text{[math]}$ 六等分，依次得到 $\text{[math]}$ 六个分点；②分别以点 $\text{[math]}$ 为圆心， $\text{[math]}$ 长为半径画弧，两弧交于点 $\text{[math]}$ ；③连结 $\text{[math]}$ .则 $\text{[math]}$ 的长是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
12. 如图，在平面直角坐标系中，直线 $\text{[math]}$ 与反比例函数 $\text{[math]}$ 的图象交于关于原点对称的 $\text{[math]}$ 两点，将直线 $\text{[math]}$ 向上平移后与反比例函数的图象在第二象限内交于点 $\text{[math]}$ ，如果 $\text{[math]}$ 的面积为48，则平移后的直线的函数表达式是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题

二、填空题

13. 我市某天的最高气温是4℃，最低气温是 $\text{[math]}$ ，则这天的日温差是℃.

查看解析收藏纠错

+选题

14. 把一枚木质中国象棋子“兵”从一定高度落下，落地后“兵”字面可能朝上，也可能朝下.为了估计“兵”字面朝上的概率，某实验小组做了棋子下掷实验数据如下表：

实验次数 $\text{[math]}$	20	60	100	120	140	160	500	1000	2000	5000
“兵”字面朝上次数 $\text{[math]}$	14	38	52	66	78	88	280	550	1100	2750
“兵”字面朝上频率 $\text{[math]}$	0.7	0.63	0.52	0.55	0.56	0.55	0.56	0.55	0.55	0.55

下面有三个推断：①投掷1000次时，“兵”字面朝上的次数是550，所以“兵”字面朝上的概率是0.55；②随着实验次数的增加，“兵”字面朝上的频率总在0.55附近，显示出一定的稳定性，可以估计“兵”字面朝上的概率是0.55；③当实验次数为200次时，“兵”字面朝上的频率一定是0.55.其中合理的是.（填序号①、②、③）

查看解析收藏纠错

+选题

15. 在平面直角坐标系中，点 $\text{[math]}$ 和 $\text{[math]}$ 在函数 $\text{[math]}$ 的图象上，若 $\text{[math]}$ ，则 $\text{[math]}$ 的取值范围是.

查看解析收藏纠错

+选题
16. 在 $\text{[math]}$ 中， $\text{[math]}$ ，点 $\text{[math]}$ 在 $\text{[math]}$ 边上， $\text{[math]}$ .若 $\text{[math]}$ ，则 $\text{[math]}$ 的长为.

查看解析收藏纠错

+选题

三、解答题

17. 如图，在长方形ABCD中无重叠放入面积分别为16 cm²和12 cm²的两张正方形纸片，求图中空白部分的面积.

查看解析收藏纠错

+选题
18. 货轮从甲港往乙港运送货物，甲港的装货速度是每小时30吨，一共装了8小时，到达乙港后开始卸货，乙港卸货的速度是每小时 $\text{[math]}$ 吨，设卸货的时间是 $\text{[math]}$ 小时

（1）当 $\text{[math]}$ 是 $\text{[math]}$ 的函数时，求 $\text{[math]}$ 与 $\text{[math]}$ 之间的函数关系式；

（2）若卸货的速度是每小时40吨，求乙港卸完全部货物所需的时间；

（3）在（2）的条件下，当卸货时间在4小时的时候，问船上剩余货物是多少吨？

查看解析收藏纠错

+选题
19. 如图，河流两岸PQ，MN互相平行，C、D是河岸PQ上间隔50m的两个电线杆，某人在河岸MN上的A处测得∠DAB＝30°，然后沿河岸走了100m到达B处，测得∠CBF＝70°，求河流的宽度（结果精确到个位， $\text{[math]}$ ＝1.73，sin70°＝0.94，cos70°＝0.34，tan70°＝2.75）

查看解析收藏纠错

+选题
20. 桃花中学计划购买A,B两种型号的小黑板，经洽谈，购买一块A型小黑板比买一块B型小黑板多20元，且购买5块A型小黑板和4块B型小黑板共需820元.

（1）求购买一块A型小黑板和一块B型小黑板各需要多少元？

（2）根据学校的实际情况，需购买 $\text{[math]}$ 两种型号的小黑板共 $\text{[math]}$ 块，并且购买 $\text{[math]}$ 型小黑板的数量不少于购买 $\text{[math]}$ 型小黑板的数量，请问学校购买这批小黑板最少要多少元？

查看解析收藏纠错

+选题
21. 如图，在正方形 $\text{[math]}$ 的对角线 $\text{[math]}$ 上取一点 $\text{[math]}$ .连接 $\text{[math]}$ 并延长 $\text{[math]}$ 到点 $\text{[math]}$ ，使 $\text{[math]}$ 与 $\text{[math]}$ 相交于点 $\text{[math]}$ .

（1）求证： $\text{[math]}$ ；

（2）若 $\text{[math]}$ ，判断 $\text{[math]}$ 之间的数量关系，并说明理由.

查看解析收藏纠错

+选题

22. 垫球是排球队常规训练的重要项目之一.下列图表中的薮据是甲，乙，丙三名校排球队员每人10次垫球测试的成绩.测试规则为每次连续接球10个，每垫球到位1个记1分.

收集整理数据：

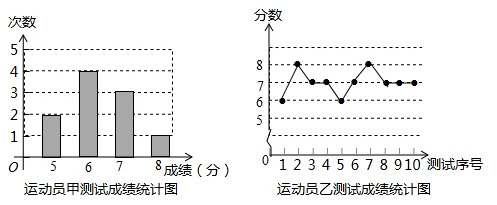
运动员丙测试成绩统计表

测试序号	1	2	3	4	5	6	7	8	9	10
成绩（分）	7	6	8	7	7	5	8	7	8	7

三人成绩的方差分别为 $\text{[math]}$ .

利用数据决策：

（1）若在三名队员中选择一位垫球成绩优秀且较为稳定的同学作为排球比赛的自由人，你认为选谁更合适？请用你所学过的统计量加以分析说明；

（2）训练期间甲、乙、丙三人之间进行随机传球游戏，先由甲传出球，经过三次传球，球回到甲手中的概率是多少？

查看解析收藏纠错

+选题

23. 如图，在矩形 $\text{[math]}$ 中， $\text{[math]}$ ，点 $\text{[math]}$ 在直线 $\text{[math]}$ 上， $\text{[math]}$ 与直线 $\text{[math]}$ 相交所成的锐角为 $\text{[math]}$ ，点 $\text{[math]}$ 在直线 $\text{[math]}$ 上， $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ ，垂足为点 $\text{[math]}$ ，且与点 $\text{[math]}$ 重合， $\text{[math]}$ ，以 $\text{[math]}$ 为直径，在 $\text{[math]}$ 的左侧作半圆 $\text{[math]}$ ，点 $\text{[math]}$ 是半圆 $\text{[math]}$ 上任意一点.

（1）连接 $\text{[math]}$ ，求线段 $\text{[math]}$ 的最大值；

（2）矩形 $\text{[math]}$ 保持不动，半圆 $\text{[math]}$ 沿直线 $\text{[math]}$ 向左平移，当点 $\text{[math]}$ 落在边 $\text{[math]}$ 上时，求半圆 $\text{[math]}$ 与矩形 $\text{[math]}$ 重合部分的面积 $\text{[math]}$ ；

（3）在平移过程中，当半圆 $\text{[math]}$ 与矩形 $\text{[math]}$ 的边相切时，求平移的距离.（参考数据： $\text{[math]}$ ，结果保留根号）.

查看解析收藏纠错

+选题
24. 二次函数 $\text{[math]}$ 的图象，与 $\text{[math]}$ 轴交于原点和点 $\text{[math]}$ ，顶点 $\text{[math]}$ 的坐标为 $\text{[math]}$ .

（1）求二次函数的表达式；

（2）大家知道二次函数的图象是一条抛物线，过 $\text{[math]}$ 两点可以画无数条抛物线，设顶点为 $\text{[math]}$ ，过点 $\text{[math]}$ 向 $\text{[math]}$ 轴、 $\text{[math]}$ 轴作垂线，垂足为点 $\text{[math]}$ .求当所得的四边形 $\text{[math]}$ 为正方形时的二次函数表达式；

（3） $\text{[math]}$ 点在（1）中求出的二次函数图象上，且 $\text{[math]}$ 点的横坐标为1， $\text{[math]}$ 点是坐标平面上一点，点 $\text{[math]}$ 在 $\text{[math]}$ 轴上，是否存在以 $\text{[math]}$ 四点为顶点的四边形是正方形，若存在，求出点 $\text{[math]}$ 的坐标；若不存在，说明理由.

查看解析收藏纠错

+选题
25. 我们约定：在一个平面图形上画一条直线，若这条直线既平分该图形的面积，又平分该图形的周长，我们称这条直线为这个图形的“等分积周线”.

（1）如图①，在 $\text{[math]}$ 中， $\text{[math]}$ ，过点 $\text{[math]}$ 能否画出 $\text{[math]}$ 的一条“等分积周线”？若能，说出你的画法；若不能，说明理由；

（2）如图②，在四边形 $\text{[math]}$ 中， $\text{[math]}$ 垂直平分 $\text{[math]}$ ，垂足为点 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ .判断直线 $\text{[math]}$ 是否为四边形 $\text{[math]}$ 的“等分积周线”，并说明理由；

（3）如图③，在 $\text{[math]}$ 中， $\text{[math]}$ ，请按要求作出 $\text{[math]}$ 的一条“等分积周线” $\text{[math]}$ ，叙述你的画法，并对你的画法进行证明要求：直线 $\text{[math]}$ 不过 $\text{[math]}$ 的顶点，交 $\text{[math]}$ 边于点 $\text{[math]}$ ，交 $\text{[math]}$ 边于点 $\text{[math]}$ .用黑色签字笔画图.

查看解析收藏纠错

+选题

贵州省贵阳市花溪区2021年数学中考模拟试卷

一、单选题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨