修改时间:2024-07-13 浏览次数:173 类型:期中考试
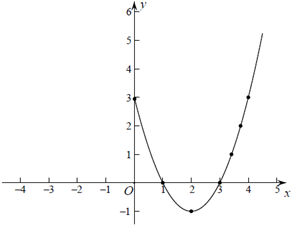
①函数图象关于y轴对称;
②函数既有最大值,也有最小值;
③当 时,y随x的增大而增大,当
时,y随x的增大而减小;
④函数图象与x轴有2个公共点.
所有正确结论的序号是.
在这个变化过程中,小明通过观察、度量,发现了一些特殊的数量关系.
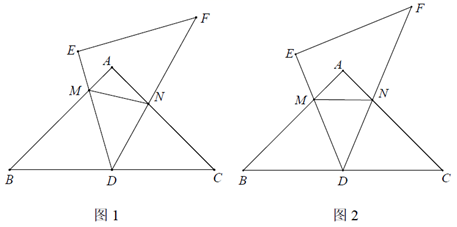
①通过计算 和
的度数,得出
(填>,<或=);
②设 ,通过计算AM、MN、NC的长度,其中
,进而得出AM、MN、NC之间的数量关系是.
试题篮