修改时间:2025-01-09 浏览次数:5 类型:单元试卷
某校学生睡眠时间各类别人数情况统计图

学生类别 | 学生平均每天睡眠时间x(单位:小时) |
A | 7≤x<7.5 |
B | 7.5≤x<8 |
C | 8≤x<8.5 |
D | 8.5≤x<9 |
E | x≥9 |
|
九年级2班参加球类活动人数统计表 |
|||||
|
项目 |
篮球 |
足球 |
乒乓球 |
排球 |
羽毛球 |
|
人数 |
a |
6 |
4 |
8 |
6 |
根据图中提供的信息,解答下列问题:

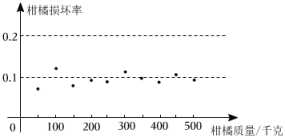
| 特级柑橘的售价(元/千克) | 14 | 15 | 16 | 17 | 18 |
| 特级柑橘的日销售量(千克) | 1000 | 850 | 900 | 850 | 800 |
试题篮