修改时间:2020-10-19 浏览次数:286 类型:期中考试
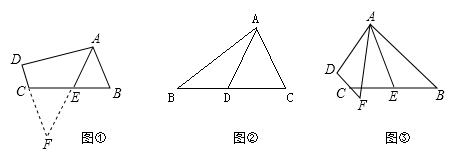
解决此问题可以用如下方法:延长AE交DC的延长线于点F,易证△AEB≌△FEC得到AB=FC,从而把AB,AD,DC转化在一个三角形中即可判断。
AB,AD,DC之间的等量关系;
①如图②,AD是△ABC的中线,AB=6,AC=4,求AD的范围:
②如图③,在四边形ABCD中,AB∥CD,AF与DC的延长线交于点F,点E是BC的中点,若AE是∠BAF的平分线,试探究AB,AF,CF之间的等量关系,并证明你的结论。
截长法与补短法在证明线段的和、差、倍、分等问题中有着广泛的应用.具体的做法是在某条线段上截取一条线段等于某特定线段,或将某条线段延长,使之与某特定线段相等,再利用全等三角形的性质等有关知识来解决数学问题.
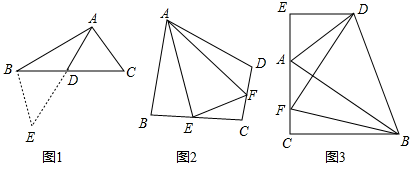
解决此问题可以用如下方法:延长AD到点E使DE=AD,再连接BE,把AB、AC、2AD集中在△ABE中.利用三角形三边的关系即可判断中线AD的取值范围是;
如图2,在四边形ABCD中,AB=AD,∠ABC+∠ADC=180°,E、F分别是边BC,边CD上的两点,且∠EAF= ∠BAD,求证:BE+DF=EF.
如图3,在△ABC中,∠ACB=90°,∠CAB=60°,点D是△ABC外角平分线上一点,DE⊥AC交CA延长线于点E,F是AC上一点,且DF=DB.求证:AC-AE= AF.
试题篮