广西南宁市2020年数学中考一模试卷

修改时间：2024-11-06 浏览次数：288 类型：中考模拟编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、单选题

1. $\text{[math]}$ 的相反数是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 6

查看解析收藏纠错

+选题
2. 如图图形中，既是轴对称图形又是中心对称图形的有（　　）

A . 1个 B . 2个 C . 3个 D . 4个

查看解析收藏纠错

+选题
3. 下列调查中，适合的是（）

A . 《新闻联播》电视栏目的收视率，采用全面调查方式 B . 为了精确调查你所在班级的同学的身高，采用抽样调查方式 C . 习主席视察长江水域建设情况，环保部门为调查长江某段水域的水质情况，采用抽样调查方式 D . 调查一个乡镇学生家庭的收入情况，采用全面调查方式

查看解析收藏纠错

+选题
4. 习近平总书记提出精准扶贫战略以来，各地积极推进精准扶贫，加大帮扶力度，全国脱贫人口数不断增加，脱贫人口接近 $\text{[math]}$ 人，将数据 $\text{[math]}$ 用科学记数法表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
5. 下列运算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$ （ $\text{[math]}$ 为正整数）

查看解析收藏纠错

+选题
6. 不等式组 $\text{[math]}$ ，的解集在数轴上表示正确的是（）

A . B . C . D .

查看解析收藏纠错

+选题
7. 如图，在菱形ABCD中，AC与BD相交于点O.将菱形沿EF折叠，使点C与点O重合.若在菱形ABCD内任取一点，则此点取自阴影部分的概率为（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
8. 如图，已知直线 $\text{[math]}$ 与 $\text{[math]}$ 相交于点 $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 的直径， $\text{[math]}$ 于点 $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ 的大小为（）

A . 12° B . 18° C . 22° D . 30°

查看解析收藏纠错

+选题
9. 某班组每天需生产50个零件才能在规定的时间内完成一批零件任务，实际上该班组每天比计划多生产了6个零件，结果比规定的时间提前3天并超额生产120个零件，若设该班组要完成的零件任务为x个，则可列方程为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
10. 如图，关于x的二次函数y=x²﹣x+m的图象交x轴的正半轴于A，B两点，交y轴的正半轴于C点，如果x=a时，y＜0，那么关于x的一次函数y=（a﹣1）x+m的图象可能是（）

A . B . C . D .

查看解析收藏纠错

+选题
11. 如图，点 $\text{[math]}$ 在半圆 $\text{[math]}$ 上，半径 $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 在弧 $\text{[math]}$ 上移动，连接 $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 上一点， $\text{[math]}$ ，连接 $\text{[math]}$ ，点 $\text{[math]}$ 在移动的过程中， $\text{[math]}$ 的最小值是（）

A . 5 B . 6 C . 7 D . 8

查看解析收藏纠错

+选题
12. 如图，点A、B是反比例函数y＝ $\text{[math]}$ （k≠0）图象上的两点，延长线段AB交y轴于点C，且点B为线段AC中点，过点A作AD⊥x轴于点D，点E为线段OD的三等分点，且OE＜DE.连接AE、BE，若S_△ABE＝7，则k的值为（）

A . ﹣12 B . ﹣10 C . ﹣9 D . ﹣6

查看解析收藏纠错

+选题

二、填空题

13. 若分式 $\text{[math]}$ 有意义，则x的取值范围为.

查看解析收藏纠错

+选题
14. 因式分解：a³+2a²+a=．

查看解析收藏纠错

+选题
15. 从数字2，3，4中任选两个数组成一个两位数，组成的数是偶数的概率是．

查看解析收藏纠错

+选题
16. 如图，在边长为2的菱形ABCD中，∠A=60°，点M是AD边的中点，连接MC，将菱形ABCD翻折，使点A落在线段CM上的点E处，折痕交AB于点N，则线段EC的长为．

查看解析收藏纠错

+选题
17.
如图，某水平地面上建筑物的高度为AB，在点D和点F处分别竖立高是2米的标杆CD和EF，两标杆相隔52米，并且建筑物AB、标杆CD和EF在同一竖直平面内，从标杆CD后退2米到点G处，在G处测得建筑物顶端A和标杆顶端C在同一条直线上；从标杆FE后退4米到点H处，在H处测得建筑物顶端A和标杆顶端E在同一条直线上，则建筑物的高是米．

查看解析收藏纠错

+选题

18. 将从1开始的连续自然数按图规律排列：

列行	第1列	第2列	第3列	第4列
第1行	1	2	3	4
第2行	8	7	6	5
第3行	9	10	11	12
第4行	16	15	14	13
…	…	…	…	…
第 $\text{[math]}$ 行	…	…	…	…

规定位于第 $\text{[math]}$ 行，第 $\text{[math]}$ 列的自然数10记为 $\text{[math]}$ ，自然数15记为 $\text{[math]}$ …按此规律，自然数2018记为.

查看解析收藏纠错

+选题

三、解答题

19. 计算： $\text{[math]}$ .

查看解析收藏纠错

+选题
20. 先化简，再求值： $\text{[math]}$ ，其中 $\text{[math]}$ 满足方程 $\text{[math]}$ .

查看解析收藏纠错

+选题
21. 如图，在平面直角坐标系中，已知 $\text{[math]}$ 的三个顶点的坐标分别为 $\text{[math]}$ .

①若 $\text{[math]}$ 经过平移后得到 $\text{[math]}$ ，已知点 $\text{[math]}$ 的坐标为 $\text{[math]}$ ，写出顶点 $\text{[math]}$ 的坐标，画出 $\text{[math]}$ ；

②若 $\text{[math]}$ 和 $\text{[math]}$ 关于原点 $\text{[math]}$ 成中心对称图形，写出 $\text{[math]}$ 的各顶点的坐标；

③将 $\text{[math]}$ 绕着点 $\text{[math]}$ 按顺时针方向旋转 $\text{[math]}$ 得到 $\text{[math]}$ ，写出 $\text{[math]}$ 的各顶点的坐标，并画出 $\text{[math]}$ .

查看解析收藏纠错

+选题

22. 某公司为了到高校招聘大学生，为此设置了三项测试：笔试、面试、实习.学生的最终成绩由笔试面试、实习依次按3：2：5的比例确定.公司初选了若干名大学生参加笔试，面试，并对他们的两项成绩分别进行了整理和分析.下面给出了部分信息：

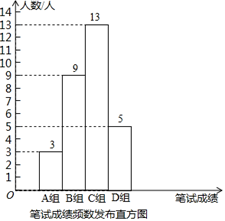
①公司将笔试成绩（百分制）分成了四组，分别为A组：60≤x＜70，B组：70≤x＜80，C组：80≤x＜90，D组：90≤x＜100；并绘制了如下的笔试成绩频数分布直方图.其中，C组的分数由低到高依次为：80，81，82，83，83，84，84，85，86，88，88，88，89.

②这些大学生的笔试、面试成绩的平均数、中位数、众数、最高分如下表：

	平均数	中位数	众数	最高分
笔试成绩	81	m	92	97
面试成绩	80.5	84	86	92

根据以上信息，回答下列问题：

（1）这批大学生中笔试成绩不低于88分的人数所占百分比为.

（2） m＝分，若甲同学参加了本次招聘，他的笔试、面试成绩都是83分，那么该同学成绩排名靠前的是成绩，理由是.

（3）乙同学也参加了本次招聘，笔试成绩虽不是最高分，但也不错，分数在D组；面试成绩为88分，实习成绩为80分由表格中的统计数据可知乙同学的笔试成绩为分；若该公司最终录用的最低分数线为86分，请通过计算说明，该同学最终能否被录用？

查看解析收藏纠错

+选题

23. 如图，已知在 $\text{[math]}$ 中， $\text{[math]}$ 是 $\text{[math]}$ 边上一点， $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 的外接圆， $\text{[math]}$ 是 $\text{[math]}$ 的直径，且交 $\text{[math]}$ 于点 $\text{[math]}$ .

（1）求证： $\text{[math]}$ 是 $\text{[math]}$ 的切线；

（2）过点 $\text{[math]}$ 作 $\text{[math]}$ ，垂足为点 $\text{[math]}$ ，延长 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，若 $\text{[math]}$ ，求 $\text{[math]}$ 的长；

（3）在满足（2）的条件下，若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的半径及 $\text{[math]}$ 的值.

查看解析收藏纠错

+选题
24. 我市“上品”房地产开发公司于2010年5月份完工一商品房小区，6月初开始销售，其中6月的销售单价为0.7万元 $\text{[math]}$ ，7月的销售单价为0.72万元 $\text{[math]}$ ，且每月销售价格 $\text{[math]}$ （单位：万元 $\text{[math]}$ ）与月份 $\text{[math]}$ （ $\text{[math]}$ ， $\text{[math]}$ 为整数）之间满足一次函数关系：每月的销售面积为 $\text{[math]}$ （单位： $\text{[math]}$ ），其中 $\text{[math]}$ .（ $\text{[math]}$ ， $\text{[math]}$ 为整数）.

（1）求 $\text{[math]}$ 与月份 $\text{[math]}$ 的函数关系式；

（2） 6~11月中，哪一个月的销售额最高？最高销售额为多少万元？

（3） 2010年11月时，因会受到即将实行的“国八条”和房产税政策的影响，该公司销售部预计12月份的销售面积会在11月销售面积基础上减少 $\text{[math]}$ ，于是决定将12月份的销售价格在11月的基础上增加 $\text{[math]}$ ，该计划顺利完成.为了尽快收回资金，2011年月公司进行降价促销，该月销售额为 $\text{[math]}$ 万元.这样12月、1月的销售额共为4618.4万元，请根据以上条件求出 $\text{[math]}$ 的值为多少？

查看解析收藏纠错

+选题
25. 菱形 $\text{[math]}$ 中， $\text{[math]}$ 为边 $\text{[math]}$ 上的点， $\text{[math]}$ 相交于点 $\text{[math]}$ .

（1）如图1，若 $\text{[math]}$ ， $\text{[math]}$ ，求证： $\text{[math]}$ ；

（2）如图2，若 $\text{[math]}$ .求证： $\text{[math]}$ ；

（3）如图3，在（1）的条件下，平移线段 $\text{[math]}$ 到 $\text{[math]}$ ，使 $\text{[math]}$ 为 $\text{[math]}$ 的中点，连接 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，若 $\text{[math]}$ ，请直接写出 $\text{[math]}$ 的长度.

查看解析收藏纠错

+选题
26. 如图所示，抛物线y＝x²+bx+c经过A、B两点，A、B两点的坐标分别为（﹣1，0）、（0，﹣3）．

（1）求抛物线的函数解析式；

（2）点E为抛物线的顶点，点C为抛物线与x轴的另一交点，点D为y轴上一点，且DC＝DE，求出点D的坐标；

（3）在第二问的条件下，在直线DE上存在点P，使得以C、D、P为顶点的三角形与△DOC相似，请你直接写出所有满足条件的点P的坐标．

查看解析收藏纠错

+选题

广西南宁市2020年数学中考一模试卷

一、单选题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨