2017年浙江省宁波市慈溪市第七区域中考数学模拟试卷

修改时间：2024-07-12 浏览次数：731 类型：中考模拟编辑

选择试卷全部试题 *点击此按钮，可全选试卷全部试题，进行试卷编辑

一、选择题

1. ﹣9的相反数是（）

A . ﹣ $\text{[math]}$ B . $\text{[math]}$ C . ﹣9 D . 9

查看解析收藏纠错

+选题
2. 下列运算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . a²•a⁴=a⁸ D . （﹣a³）²=a⁶

查看解析收藏纠错

+选题
3. 在以下永洁环保、绿色食品、节能、绿色环保四个标志中，是轴对称图形是（　　）

A . B . C . D .

查看解析收藏纠错

+选题
4. PM2.5是指大气中直径小于或等于0.0000025m的颗粒物，将0.0000025用科学记数法表示为（）

A . 0.25×10^﹣⁵ B . 0.25×10^﹣⁶ C . 2.5×10^﹣⁵ D . 2.5×10^﹣⁶

查看解析收藏纠错

+选题
5. 若一个多边形的每个外角都等于45°，则它的内角和等于（）

A . 720° B . 1040° C . 1080° D . 540°

查看解析收藏纠错

+选题
6. 如图，两个同心圆的半径分别为4cm和5cm，大圆的一条弦AB与小圆相切，则弦AB的长为（）

A . 6cm B . 4cm C . 3cm D . 8cm

查看解析收藏纠错

+选题
7. 如图，由五个小正方体组成的几何体中，若每个小正方体的棱长都是1，则该几何体的主视图和左视图的面积之和是（）

A . 11 B . 8 C . 7 D . 6

查看解析收藏纠错

+选题
8. 如图，在△ABC中，∠ABC和∠ACB的平分线交于点E，过点E作MN∥BC交AB于M，交AC于N，若BM+CN=9，则线段MN的长为（）

A . 6 B . 7 C . 8 D . 9

查看解析收藏纠错

+选题
9. 一名射击运动员连续打靶8次，命中的环数如图所示，则命中环数的众数与中位数分别为（）

A . 9环与8环 B . 8环与9环 C . 8环与8.5环 D . 8.5环与9环

查看解析收藏纠错

+选题
10. 在Rt△ABC中，∠C=90°，sinA= $\text{[math]}$ ，AB=5，则边AC的长是（）

A . 3 B . 4 C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
11. 如图，在直角坐标系xOy中，A（﹣4，0），B（0，2），连结AB并延长到C，连结CO，若△COB∽△CAO，则点C的坐标为（）

A . （1， $\text{[math]}$ ） B . （ $\text{[math]}$ ， $\text{[math]}$ ） C . （ $\text{[math]}$ ，2 $\text{[math]}$ ） D . （ $\text{[math]}$ ，2 $\text{[math]}$ ）

查看解析收藏纠错

+选题
12. 如图，对正方形纸片ABCD进行如下操作：
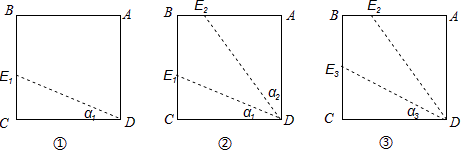
（i）过点D任作一条直线与BC边相交于点E₁（如图①），记∠CDE₁=α₁；
（ii）作∠ADE₁的平分线交AB边于点E₂（如图②），记∠ADE₂=α₂；
（iii）作∠CDE₂的平分线交BC边于点E₃（如图③），记∠CDE₃=α₃；
按此作法从操作（2）起重复以上步骤，得到α₁ ， α₂ ， …，α_n ， …，现有如下结论：①当α₁=10°时，α₂=40°；②2α₄+α₃=90°； ③当α₅=30°时，△CDE₉≌△ADE₁₀；④当α₁=45°时，BE₂= $\text{[math]}$ ．
其中正确的个数为（）

A . 1 B . 2 C . 3 D . 4

查看解析收藏纠错

+选题

二、填空题

13. 若式子 $\text{[math]}$ 在实数范围内有意义，则x的取值范围是．

查看解析收藏纠错

+选题
14. 一个等腰三角形两边的长分别为3和8，那么这个三角形的周长是．

查看解析收藏纠错

+选题
15. 如果圆锥的底面半径为2，母线长为6，那么这个圆锥的侧面积是

查看解析收藏纠错

+选题
16. 从3、﹣1、﹣2三个数中任意选取一个作为直线y=kx+2中的k值，则所得的直线不经过第三象限的概率是．

查看解析收藏纠错

+选题
17. 如图，在平面直角坐标系中，O为坐标原点，平行四边形ABOC的对角线交于点M，双曲线y= $\text{[math]}$ （x＜0）经过点B、M．若平行四边形ABOC的面积为12，则k=．

查看解析收藏纠错

+选题
18. 如图，AB是⊙O的直径，AC是切⊙O于A的切线，BC交⊙O于点D，E是劣弧 $\text{[math]}$ 的中点，连接AE交BC于点F，若cosC= $\text{[math]}$ ，AC=6，则BF的长为．

查看解析收藏纠错

+选题

三、解答题

19. 解方程： $\text{[math]}$ = $\text{[math]}$ ．

查看解析收藏纠错

+选题
20.
如图，在平面直角坐标系xOy中，△ABC的三个顶点坐标分别为A（1，1），B（4，0），C（4，4）．

（1）按下列要求作图：
①将△ABC向左平移4个单位，得到△A₁B₁C₁；
②将△A₁B₁C₁绕点B₁逆时针旋转90°，得到△A₂B₂C₂ ．

（2）求点C₁在旋转过程中所经过的路径长．

查看解析收藏纠错

+选题
21. 随着互联网、移动终端的迅速发展，数字化阅读越来越普及，公交上的“低头族”越来越多．某研究机构针对“您如何看待数字化阅读”问题进行了随机问卷调查（如图1），并将调查结果绘制成图2和图3所示的统计图（均不完整）．请根据统计图中提供的信息，解答下列问题：

（1）求出本次接受调查的总人数，并将条形统计图补充完整；

（2）表示观点B的扇形的圆心角度数为度；

（3） 2016年底慈溪人口总数约为200万（含外来务工人员），请根据图中信息，估计慈溪市民认同观点D的人数．

查看解析收藏纠错

+选题
22. 如图所示，在⊙O中， $\text{[math]}$ = $\text{[math]}$ ，弦AB与弦AC交于点A，弦CD与AB交于点F，连接BC．

（1）求证：AC²=AB•AF；

（2）若⊙O的半径长为2cm，∠B=60°，求图中阴影部分面积．

查看解析收藏纠错

+选题
23.
按照有关规定：距高铁轨道 200米以内的区域内不宜临路新建学校、医院、敬老院和集中住宅区等噪声敏感建筑物．
如图是一个小区平面示意图，矩形ABEF为一新建小区，直线MN为高铁轨道，C、D是直线MN上的两点，点C、A、B在一直线上，且DA⊥CA，∠ACD=30°．小王看中了①号楼A单元的一套住宅，与售楼人员的对话如下：

（1）小王心中一算，发现售楼人员的话不可信，请你用所学的数学知识说明理由；

（2）若一列长度为228米的高铁以252千米/小时的速度通过时，则A单元用户受到影响时间有多长？
（温馨提示： $\text{[math]}$ ≈1.4， $\text{[math]}$ ≈1.7， $\text{[math]}$ ≈6.1）

查看解析收藏纠错

+选题
24. 我市某校为了创建书香校园，去年购进一批图书．经了解，科普书的单价比文学书的单价多4元，用12000元购进的科普书与用8000元购进的文学书本数相等．今年文学书和科普书的单价与去年相比保持不变，该校打算用10000元再购进一批文学书和科普书，问购进文学书550本后至多还能购进多少本科普书？

查看解析收藏纠错

+选题
25.
定义：如图1，点M，N把线段AB分割成AM，MN和BN，若以AM，MN，BN为边的三角形是一个直角三角形，则称点M，N是线段AB的勾股分割点

（1）已知点M，N是线段AB的勾股分割点，若AM=3，MN=4求BN的长；

（2）已知点C是线段AB上的一定点，其位置如图2所示，请在BC上画一点D，使C，D是线段AB的勾股分割点（要求尺规作图，保留作图痕迹，画出一种情形即可）

（3）
如图3，正方形ABCD中，M，N分别在BC，DC上，且BM≠DN，∠MAN=45°，AM，AN分别交BD于E，F
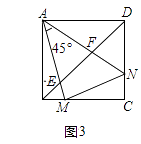
求证：①E、F是线段BD的勾股分割点；
②△AMN的面积是△AEF面积的两倍．

查看解析收藏纠错

+选题
26.
如图，在平面直角坐标系中，直线y= $\text{[math]}$ x+1与抛物线y=ax²+bx﹣3交于A，B两点，点A在x轴上，点B的纵坐标为3．点P是直线AB下方的抛物线上一动点（不与A，B重合），过点P作x轴的垂线交直线AB与点C，作PD⊥AB于点D

（1） ①求抛物线的解析式；②求sin∠ACP的值

（2）设点P的横坐标为m
①用含m的代数式表示线段PD的长，并求出线段PD长的最大值；
②连接PB，线段PC把△PDB分成两个三角形，求出当这两个三角形面积之比为9：10时的m值；
③是否存在适合的m值，使△PCD与△PBD相似？若存在，直接写出m值；若不存在，说明理由．

查看解析收藏纠错

+选题

2017年浙江省宁波市慈溪市第七区域中考数学模拟试卷

一、选择题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨