浙江省杭州市2018届数学中考模拟试卷（6月份）

1. ﹣9的绝对值是（）

A . ﹣9 B . 9 C . $\text{[math]}$ D .

查看解析收藏纠错

+选题
2. 我市今年参加中考人数约为42000人，将42000用科学记数法表示为（）

A . 4.2×10⁴ B . 0.42×10⁵ C . 4.2×10³ D . 42×10³

查看解析收藏纠错

+选题
3. 在实数范围内，下列判断正确的是（）

A . 若，则a=b B . 若|a|=（ $\text{[math]}$ ）² ，则a=b C . 若a＞b，则a²＞b² D . 若（ $\text{[math]}$ ）²=（ $\text{[math]}$ ）²则a=b

查看解析收藏纠错

+选题
4. 已知数据1、5、4、3、3、2，则下列关于这组数据的说法错误的是（）

A . 平均数和众数都是3 B . 中位数为3 C . 方差为10 D . 标准差是

查看解析收藏纠错

+选题
5. 如图所示，直线AB与直线CD相交于点O，EO⊥AB，∠EOD=25°，则下列说法正确的是（）

A . ∠AOE与∠BOC互为对顶角 B . 图中有两个角是∠EOD的邻补角 C . 线段DO大于EO的理由是垂线段最短 D . ∠AOC=65°

查看解析收藏纠错

+选题
6. 如图为某商店的宣传单，小胜到此店同时购买了一件标价为x元的衣服和一条标价为y元的裤子，共节省500元，则根据题意所列方程正确的是（）

A . 0.6x+0.4y+100=500 B . 0.6x+0.4y﹣100=500 C . 0.4x+0.6y+100=500 D . 0.4x+0.6y﹣100=500

查看解析收藏纠错

+选题
7. 在一个不透明的口袋里有红、黄、蓝三种颜色的小球，这些球除颜色外都相同，其中有5个红球，4个蓝球．若随机摸出一个蓝球的概率为 $\text{[math]}$ ，则随机摸出一个黄球的概率为（）

A . $\text{[math]}$ B . C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
8. 如图，点P是矩形ABCD的边上一动点，矩形两边长AB，BC长分别为3和4，那么P到矩形两条对角线AC和BD的距离之和是（）

A . B . $\text{[math]}$ C . D . 不确定

查看解析收藏纠错

+选题
9. 二次函数y=ax²+bx+c（a、b、c为常数，且a≠0）中x与y的部分对应值如下表：

x

﹣2

﹣1

0

1

2

3

4

y

5

0

﹣3

﹣4

﹣3

0

5

给出以下三个结论：（1）二次函数y=ax²+bx+c最小值为﹣4；（2）若y＜0，则x的取值范围是0＜x＜2；（3）二次函数y=ax²+bx+c的图象与x轴有两个交点，且它们分别在y轴两侧，则其中正确结论的个数是（）

A . 0 B . 1 C . 2 D . 3

查看解析收藏纠错

+选题
10. 如图，△ABC，△FGH中，D，E两点分别在AB，AC上，F点在DE上，G、H两点在BC上，且DE∥BC，FG∥AB，FH∥AC，若BG：GH：HC=4：6：5，则△ADE与△FGH的面积比为何？（）

A . 2：1 B . 3：2 C . 5：2 D . 9：4

查看解析收藏纠错

+选题

11. 已知单项式3a^mb²与﹣ $\text{[math]}$ a⁴bⁿ^﹣¹的和是单项式，那么2m﹣n=．

查看解析收藏纠错

+选题
12. 如图，a∥b，∠1=110°，∠3=40°，则∠2=°

查看解析收藏纠错

+选题
13. 分解因式：9abc-3ac²=．

查看解析收藏纠错

+选题
14. 如图，点A、B、C都在⊙O上，OC⊥OB，点A在劣弧 $\text{[math]}$ 上，且OA=AB，则∠ABC=．

查看解析收藏纠错

+选题
15. 星期天，小明上午8：00从家里出发，骑车到图书馆去借书，再骑车回到家．他离家的距离y（千米）与时间t（分钟）的关系如图所示，则上午8：45小明离家的距离是千米．

查看解析收藏纠错

+选题
16. 如图，矩形ABCD中，AD=10，AB=8，点E为边DC上一动点，连接AE，把△ADE沿AE折叠，使点D落在点D′处，当△DD′C是直角三角形时，DE的长为．

查看解析收藏纠错

+选题

17. 家用电灭蚊器的发热部分使用了PTC发热材料，它的电阻R（kΩ）随温度t（℃）（在一定范围内）变化的大致图象如图所示．通电后，发热材料的温度在由室温10℃上升到30℃的过程中，电阻与温度成反例关系，且在温度达到30℃时，电阻下降到最小值；随后电阻承温度升高而增加，温度每上升1℃，电阻增加 $\text{[math]}$ kΩ．

（1）求R和t之间的关系式；

（2）家用电灭蚊器在使用过程中，温度在什么范围内时，发热材料的电阻不超过4kΩ．

查看解析收藏纠错

+选题

18. 某校七年级1班体育委员统计了全班同学60秒跳绳的次数，并绘制出如下频数分布表和频数分布直方图：

次数	80≤x＜100	100≤x＜120	120≤x＜140	140≤x＜160	160≤x＜180	180≤x＜200
频数	a	4	12	16	8	3

结合图表完成下列问题：

（1） a=；

（2）补全频数分布直方图；

（3）写出全班人数是，并求出第三组“120≤x＜140”的频率（精确到0.01）

（4）若跳绳次数不少于140的学生成绩为优秀，则优秀学生人数占全班总人数的百分之几？

查看解析收藏纠错

+选题

19. 已知：如图，在△ABC中，AB=AC=5，BC=8，D，E分别为BC，AB边上一点，∠ADE=∠C．

（1）求证：△BDE∽△CAD；

（2）若CD=2，求BE的长．

查看解析收藏纠错

+选题
20. 对于实数a，b，我们可以用min{a，b}表示a，b两数中较小的数，例如min{3，﹣1}=﹣1，min{2，2}=2．类似地，若函数y₁、y₂都是x的函数，则y=min{y₁ ， y₂}表示函数y₁和y₂的“取小函数”．

（1）设y₁=x，y₂= $\text{[math]}$ ，则函数y=min{x， $\text{[math]}$ }的图象应该是中的实线部分．

（2）请在图1中用粗实线描出函数y=min{（x﹣2）² ，（x+2）²}的图象，并写出该图象的三条不同性质：
①；②；③；

（3）函数y=min{（x﹣4）² ，（x+2）²}的图象关于对称．

查看解析收藏纠错

+选题
21. 如图，在直角三角形ABC中，∠ACB=90°，CD是AB边上的高，AB=10cm，BC=8cm，AC=6cm，求：

（1） CD的长；

（2） △ABC的角平分线AE交CD于点F，交BC于E点，求证：∠CFE=∠CEF．

查看解析收藏纠错

+选题
22. 如图，抛物线y＝ax²＋ $\text{[math]}$ x＋c（a≠0）与x轴交于点A，B两点，其中A(－1，0)，与y轴交于点C(0，2)．

（1）求抛物线的表达式及点B坐标；

（2）点E是线段BC上的任意一点（点E与B、C不重合），过点E作平行于y轴的直线交抛物线于点F，交x轴于点G．
①设点E的横坐标为m，用含有m的代数式表示线段EF的长；

②线段EF长的最大值是．

查看解析收藏纠错

+选题
23. 阅读下列材料，完成任务：
自相似图形

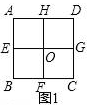
定义：若某个图形可分割为若干个都与它相似的图形，则称这个图形是自相似图形．例如：正方形ABCD中，点E、F、G、H分别是AB、BC、CD、DA边的中点，连接EG，HF交于点O，易知分割成的四个四边形AEOH、EBFO、OFCG、HOGD均为正方形，且与原正方形相似，故正方形是自相似图形．

任务：

（1）图1中正方形ABCD分割成的四个小正方形中，每个正方形与原正方形的相似比为；

（2）如图2，已知△ABC中，∠ACB=90°，AC=4，BC=3，小明发现△ABC也是“自相似图形”，他的思路是：过点C作CD⊥AB于点D，则CD将△ABC分割成2个与它自己相似的小直角三角形．已知△ACD∽△ABC，则△ACD与△ABC的相似比为；

（3）现有一个矩形ABCD是自相似图形，其中长AD=a，宽AB=b（a＞b）．
请从下列A、B两题中任选一条作答：我选择题．

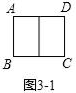
A：①如图3﹣1，若将矩形ABCD纵向分割成两个全等矩形，且与原矩形都相似，则a=（用含b的式子表示）；

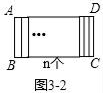
②如图3﹣2若将矩形ABCD纵向分割成n个全等矩形，且与原矩形都相似，则a=（用含n，b的式子表示）；

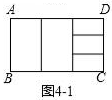
B：①如图4﹣1，若将矩形ABCD先纵向分割出2个全等矩形，再将剩余的部分横向分割成3个全等矩形，且分割得到的矩形与原矩形都相似，则a=（用含b的式子表示）；

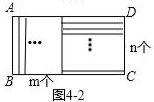
②如图4﹣2，若将矩形ABCD先纵向分割出m个全等矩形，再将剩余的部分横向分割成n个全等矩形，且分割得到的矩形与原矩形都相似，则a=（用含m，n，b的式子表示）．

查看解析收藏纠错

+选题

浙江省杭州市2018届数学中考模拟试卷（6月份）

一、单选题

二、填空题

三、解答题

相关试卷收起∨

x	﹣2	﹣1	0	1	2	3	4
y	5	0	﹣3	﹣4	﹣3	0	5

浙江省杭州市2018届数学中考模拟试卷（6月份）

一、单选题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨