河南省南阳市唐河县2018届九年级上学期数学期末考试试卷

1. 下列运算中正确的是（）

A . $\text{[math]}$ ﹣ = $\text{[math]}$ B . 2 $\text{[math]}$ +3 $\text{[math]}$ =6 $\text{[math]}$ C . $\text{[math]}$ ÷ = $\text{[math]}$ D . （ +1）（ ﹣1）=3

查看解析收藏纠错

+选题
2. 下列各组线段的长度成比例的是（）

A . 6cm、2cm、1cm、4cm B . 4cm、5cm、6cm、7cm C . 3cm、4cm、5cm、6cm D . 6cm、3cm、8cm、4cm

查看解析收藏纠错

+选题
3. 已知关于x的方程kx²+(1-k)x-1=0，下列说法正确的是（）.

A . 当时，方程无解 B . 当 $\text{[math]}$ 时，方程有两个相等的实数解 C . 当时，方程有一个实数解 D . 当时，方程总有两个不相等的实数解

查看解析收藏纠错

+选题
4. 在一幅长80cm，宽50cm的矩形风景画的四周镶上一条金色纸边，制成一幅矩形挂图，如果要使整个挂图的面积是5000cm² ，设金色纸边的宽为xcm，那么满足的方程是（）

A . x²+130x﹣1400=0 B . x²﹣130x﹣1400=0 C . x²+65x﹣250=0 D . x²﹣65x﹣250=0

查看解析收藏纠错

+选题
5. 如图，△ABC中，DE∥BC， $\text{[math]}$ = $\text{[math]}$ ，则OE：OB=（）

A . $\text{[math]}$ B . C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
6. 如图，在 $\text{[math]}$ 的正方形方格中， $\text{[math]}$ 的顶点都在边长为 $\text{[math]}$ 的小正方形的顶点上，作一个与 $\text{[math]}$ 相似的 $\text{[math]}$ ，使它的三个顶点都在小正方形的顶点上，则 $\text{[math]}$ 的最大面积是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

查看解析收藏纠错

+选题
7. 如图，在菱形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的值是（）

A . $\text{[math]}$ B . 2 C . 10 $\text{[math]}$ D .

查看解析收藏纠错

+选题
8. 如图，在平面直角坐标系中，已知A，B，C三点的坐标分别为（﹣3，﹣1）、（﹣3，﹣3）、（6，2），且△AOB∽△COD，点P（﹣3，m）是线段AB上一点，直线PO交线段CD于点Q，则点Q的纵坐标为（）

A . m B . 2m C . ﹣m D . ﹣2m

查看解析收藏纠错

+选题
9. 如图，在△ABC中，AB=AC=3，BC=4，点D，E分别是边AB，BC上点，连结DE，将△BDE沿DE翻折得到△FDE，点B的对称点F恰好落在边AC上，若以点C，E，F为顶点的三角形与△ABC相似，则BE的长为（）

A . 2 B . C . 或2 D . $\text{[math]}$ 或2

查看解析收藏纠错

+选题
10. 二次函数y=ax²+bx+c（a≠0）的图象如图所示，下列结论：①2a+b＞0；②abc＜0；③b²﹣4ac＞0；④a+b+c＜0；⑤4a﹣2b+c＜0，其中正确的个数是（）

A . 2 B . 3 C . 4 D . 5

查看解析收藏纠错

+选题

11. 计算：（ $\text{[math]}$ ）⁰﹣4sin45°tan45°+（ $\text{[math]}$ ）^﹣¹• $\text{[math]}$ +（﹣1）²⁰¹⁷+ $\text{[math]}$ =．

查看解析收藏纠错

+选题
12. 在一个不透明的盒子中，装有3个分别写有数字6，﹣2，7的小球，他们的形状、大小、质地完全相同，搅拌均匀后，先从盒子里随机抽取1个小球，记下小球上的数字后放回盒子，搅拌均匀后再随机取出1个小球，再记下小球上的数字．则两次取出的小球上的数字相同的概率是．

查看解析收藏纠错

+选题
13. 抛物线y=ax²+bx+c上部分点的横坐标x，纵坐标y的对应值如下表：

x

…

﹣2

﹣1

0

1

2

…

y

…

0

4

6

6

4

…

从上表可知，下列说法中正确的是．（填写序号）

①抛物线与x轴的一个交点为（3，0）； ②函数y=ax²+bx+c的最大值为6；

③抛物线的对称轴是直线x= $\text{[math]}$ ；④在对称轴左侧，y随x增大而增大．

查看解析收藏纠错

+选题
14. 如图，在平面直角坐标系中，将矩形AOCD沿直线AE折叠（点E在边DC上），折叠后顶点D恰好落在边OC上的点F处，已知AD=3，当点F为线段OC的三等分点时，点E的坐标为．

查看解析收藏纠错

+选题

15.

（1）解方程：2x²+x﹣6=0；

（2）阅读理解：为解方程（x²﹣1）²﹣5（x²﹣1）+4=0，我们可以将x²﹣1视为一个整体，然后设x²﹣1=y，则原方程化为y²﹣5y+4=0，解此方程得：y₁=1，y₂=4．当y=1时，x²﹣1=1，x=± $\text{[math]}$ ；当y=4时，x²﹣1=4，∴x=± $\text{[math]}$
∴原方程的解为：x₁= $\text{[math]}$ ，x₂=﹣ $\text{[math]}$ ，x₂= $\text{[math]}$ ，x₁=﹣ $\text{[math]}$

以上方法叫做换元法解方程，达到了降次的目的，体现了转化思想．

运用上述方法解方程：x⁴﹣8x²+12=0．

查看解析收藏纠错

+选题
16. 如图，在△ABC中，AB=AC，点P、D分别是BC、AC边上的点，且∠APD=∠B．

（1）求证：AC•CD=CP•BP；

（2）若AB=10，BC=12，当PD∥AB时，求BP的长．

查看解析收藏纠错

+选题
17. 自主学习，请阅读下列解题过程．
解一元二次不等式：x²﹣5x＞0．

解：设x²﹣5x=0，解得：x₁=0，x₂=5，则抛物线y=x²﹣5x与x轴的交点坐标为（0，0）和（5，0）．画出二次函数y=x²﹣5x的大致图象（如图所示），由图象可知：当x＜0，或x＞5时函数图象位于x轴上方，此时y＞0，即x²﹣5x＞0，所以，一元二次不等式x²﹣5x＞0的解集为：x＜0，或x＞5．

通过对上述解题过程的学习，按其解题的思路和方法解答下列问题：

（1）上述解题过程中，渗透了下列数学思想中的和．（只填序号）
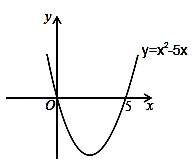
①转化思想 ②分类讨论思想 ③数形结合思想

（2）一元二次不等式x²﹣5x＜0的解集为．

（3）用类似的方法解一元二次不等式：x²﹣2x﹣3＞0．

查看解析收藏纠错

+选题
18. 某兴趣小组为了了解本校学生参加课外体育锻炼情况，随机抽取本校40名学生进行问卷调查，统计整理并绘制了如下两幅尚不完整的统计图：

根据以上信息解答下列问题：

（1）课外体育锻炼情况统计图中，“经常参加”所对应的圆心角的度数为；“经常参加课外体育锻炼的学生最喜欢的一种项目”中，喜欢足球的人数有人，补全条形统计图．

（2）该校共有1200名学生，请估计全校学生中经常参加课外体育锻炼并喜欢的项目是乒乓球的人数有多少人？

（3）若在“乒乓球”、“篮球”、“足球”、“羽毛球”项目中任选两个项目成立兴趣小组，请用列表法或画树状图的方法求恰好选中“乒乓球”、“篮球”这两个项目的概率．

查看解析收藏纠错

+选题
19. 如图，防洪大堤的横断面是梯形，背水坡AB的坡度i=1： $\text{[math]}$ ，且AB=20m．身高为1.7m的小明站在大堤A点，测得高压电线杆顶端点D的仰角为30°．已知地面CB宽30m，求小明到电线杆的距离和高压电线杆CD的高度（结果保留根号）.

查看解析收藏纠错

+选题
20. 某商店经销一种成本为每千克40元的水产品，据市场分析，若按每千克50元销售，一个月能售出500千克．若销售价每涨1元，则月销售量减少10千克．

（1）要使月销售利润达到最大，销售单价应定为多少元？

（2）要使月销售利润不低于8000元，请画出草图结合图象说明销售单价应如何定？

查看解析收藏纠错

+选题
21. 等腰Rt△PAB中，∠PAB=90°，点C是AB上一点（与A、B不重合），连接PC，将线段PC绕点C顺时针旋转90°，得到线段DC．连接PD，BD．探究∠PBD的度数，以及线段AB与BD、BC的数量关系．

（1）尝试探究：如图（1），点C在线段AB上，
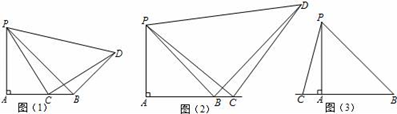
∵△PCD为等腰直角三角形，且∠PCD=90°，∴∠CPD=45°=∠APB，

∴∠CPD﹣∠BPC=∠APB﹣∠BPC，即∠BPD=∠APC，

又∵ $\text{[math]}$ ，∴△PAC∽△PBD，相似比为 $\text{[math]}$ ，∴ $\text{[math]}$ .

∴∠PBD= ；AB=BC+AC=．

（2）类比探索：如图（2），点C在直线AB上，且在点B右侧，还能得出与（1）中同样的结论么？请写出你得到的结论并证明

（3）拓展迁移：如图（3），点C在直线AB上，且在点A左侧，请补充完成图形，并直接写出你得到的结论（不需要证明）

查看解析收藏纠错

+选题
22. 如图1，直线l：y=﹣x+5与抛物线y=x²+bx+c交于坐标轴上两点B，C，且抛物线与x轴另一交点为点A．

（1）求抛物线解析式；

（2）若将直线l向下平移m个单位长度后，得到的直线l'与抛物线只有一个公共点D，求m的值及D点坐标；

（3）取BC中点N，过点N作MN∥y轴交抛物线于点M，如图2．若点P是坐标轴上一点，是否存在以C，B，P为顶点的三角形与△CMN相似？若存在，请直接写出点P的坐标；若不存在，请说明理由．

查看解析收藏纠错

+选题

河南省南阳市唐河县2018届九年级上学期数学期末考试试卷

一、单选题

二、填空题

三、解答题

相关试卷收起∨

x	…	﹣2	﹣1	0	1	2	…
y	…	0	4	6	6	4	…

河南省南阳市唐河县2018届九年级上学期数学期末考试试卷

一、单选题

二、填空题

三、解答题

相关试卷 收起∨

相关试卷收起∨